Вопрос 36. Дискретизация сигнала во времени. Теорема Котельникова

 

6.10 Дискретизация сигналов по времени

 

Было установлено, что энтропия непрерывного сигнала зависит от точности его воспроизведения. При этом рассматривались различные подходы к определению количества информации, содержащейся в отдельно взятом отчете сигнале X(t) в некоторый фиксированный момент времени t₁, представляющий собой сечение случайного процесса X(t₁).  

Для определения энтропии отсчета X(t₁) по  ранее полученным формулам, в частности по формуле

где H^*{X(t₁)} – приведенная энтропия отсчета X(t₁); Dx – интервал неопределенности; достаточно знать одновременный закон распределения случайного процесса X(t).

Если же взять отсчеты X(t₁) и X(t₂) сигнала X(t) в моменты времени t₁ и t₂, отстоящие друг от друга на интервал времени Dt=t₂–t_1, то энтропия объединения двух сигналов X(t₁) и X(t₂) в общем случае не равна сумме этих безусловных энтропий, а,  как было показано, равна энтропии первого отсчета плюс условная энтропия второго отсчета, вычисленная при условии, что первый отсчет известен. Для вычисления энтропии объединения двух отсчетов требуется уже двумерный закон распределения случайного процесса X(t). В общем случае для вычисления энтропии объединения n отсчетов сигнала требуется знать n-мерный закон распределения случайного процесса X(t).

Интуиция подсказывает, что если интервал Dt выбирать достаточно большим (больше интервал корреляции), то отсчеты X(t₁) и X(t₂) будут практически независимы и суммарное количество информации, содержащееся в этих двух отчетах, будет равно сумме их безусловных энтропий. С другой стороны, при  малом значении интервала  Dt (много меньше интервала корреляции) отсчеты X(t₁) и X(t₂) будут полностью зависимы и, следовательно, энтропия объединения двух отсчетов практически будет равна энтропии одного из этих отсчетов.

На основании вышеизложенного можно предположить, что существует некоторый оптимальный интервал Dt такой, что при длительности сигнала X(t), равной T, он позволяет представить этот сигнал его отсчетами, взятыми через интервал Dt, где n=T/Dt. При этом оптимальность интервала понимается в том смысле, что выбор значения интервала Dt больше оптимального приведет к потере информации,  уменьшение значения Dt (увеличение числа отсчетов на промежутке T) по сравнению с оптимальным не приведет к росту информационного содержания совокупности  отсчетов.

 

6.11 Теорема Котельникова

 

Оптимальный интервал Dt позволяет определить теорема Котельникова. Пусть x(t) есть реализация сигнала X(t), обладающая ограниченным спектром, т.е. полоса частот не выходит за верхнюю граничную частоту F. Для такой функции времени справедлива теорема Котельникова:

Докажем эту теорему. Пусть S(f) есть спектр реализации x(t). Поскольку функция S(f) ограничена в частотной области, она может быть представлена в форме комплексного ряда Фурье с периодом от –F до +F, коэффициенты разложения каждого определяются по формуле.

где k=0, ±1, ±2 ….

Реализация x(t)  связана со своим спектр S(f) интервальным преобразованием Фурье:

Сравнивая последнее выражения, находим, что коэффициенты разложения комплексного ряда Фурье представляют собой не что иное, как мгновение значения x[k/2F] функции x(t) в момент времени t= k/2F.

Этим, собственно, и доказывается теорема отсчетов. Остается вопрос, каким образом восстановить функцию x(t)  по ее дискретным отсчетам  x[k/2F], если в этом возникнет необходимость.

Подставив вместо функции S(f) ее представление в виде ряда Фурье, получим:

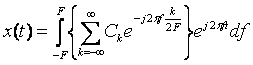
Проинтегрировав последнее выражение и заменив коэффициенты разложения C_k на соответствующие равные им отсчеты x[k/2F], окончательно именем:

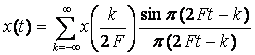
Таким образом, при k=–¥ становится очевидным, что реализация x(t) полностью определяется совокупностью отсчетов, взятых в момент времени K/2F и отстающих друг от друга на величину 1/(2F). Кроме того, представляя собой разложение по координационным функциям , функция x(t) может быть восстановлена по совокупности своих отсчетов.

На практике интерес представляют сигналы, ограниченные временным интервалом T. Оба уровня – ограничение ширины спектра и ограниченности длины сигнала – одновременно в точности выполнены быть не могут. Отсюда следует, что ограниченные во времени сигналы нельзя точно представить рядом. Так для конечных по длительности сигналов всегда возможно выбрать граничную частоту F таким образом, что за ее пределами влияние частотных составляющих сигнала на его информационную способность будет пренебрежимо мало. При этом условии реализация конечной длительности T может быть с достаточной точностью определена числом 2FT своих независимых отсчетов. Полученные результаты относительно возможности представления реализации сигнала x(t) дискретной совокупностью мгновенных значений этой функции обычно переносят непосредственно на сигнал X(t) как случайный процесс. При этом полагают, что не отрезке временем Т процесс может быть представлен числом 2FT независимых сечений, отстающих друг от друга на 1/(2F). Здесь под величиной F понимается эффективная ширина  спектра сигнала.

Такое представление, вообще говоря, не вполне верно хотя уже потому, что сечения случайного процесса на конечном интервале времени Т в общем случае не является независимыми. Тем не менее данный подход в какой-то мере оправдан, поскольку зависимость межу сечениями случайного процесса, отстоящими друг от друга на 1/(2F), во многих случаях настолько мала, что ею без особого ущерба можно пренебречь. Тогда непрерывный случайный процесс X(t), ограниченный интервалом Т и шириной полосы F, может быть представлен эквивалентной ему последовательностью независимых случайных величин X(t₀), X(t₁), X(t₂), …, X(t_k), …, X(t_n), соответствующих сечениям процесса в момент времени t_k=k/(2F).

Рассмотрим пример стационарного процесса X(t), спектральная плотность мощность G(f) которого постоянна в полосе частот от –F и +F герц (рис. 16).

 

Рис. 16 Спектральная плотность мощности        Рис. 17 Корреляционная функция

 

Корреляционная функция данного случайного процесса (рис. 17) описывается выражением:

Из графиков видно, что K(t) обращается в нуль при значениях аргумента, равных 1/(2F), 2/(2F), 3/(2F), …, k/(2F), …. Это означает, что сечения процесса, отстающие друг от друга точно на интервал k/(2F), не коррелированны между собой.

Покажем, какое количество информации содержит сигнал, описываемый непрерывным стационарным случайным процессом длительности Т, все частоты которого находятся в полосе частот от 0 до F.

Для такого сигнала независимые отсчеты обладают одинаковой энтропией, поскольку соответствующие сечения случайного процесса описываются одним и тем же одномерным законом распределения. Исходя из этого и пользуясь полученными результатами, заключаем, что количество информации, содержащейся в сигнале длительностью Т и полосой частот F,