Вопрос 31. Количество информации при измерении физических величин

 

3.3. Количество информации при измерениях физических величин

 

При измерениях увеличению информации соответствует уменьшение неопределенности исследуемого объекта. Простейшей математической моделью источника информации (О) является дискретная последовательность   независимых   значений   измеряемой   величины  {x}

(рис. 4)

 

 

 

 

 

 

 

Рис. 4. Схема измерения физических величин

 

 

Обращаясь к исходной формулировке степени неопределенности исследуемого объекта, можно отметить, что результат измерения должен уменьшить первоначальную неопределенность равновероятных состояний до некоторой конечной.

В процессе измерения на выходе измерительного устройства И образуется последовательность значений измерительного сигнала {y}, которой будут соответствовать свои величины вероятности p(y). Между последовательностями {у}  измерительного сигнала и значениями измеряемой величины {х} должна иметь место некоторая статистическая связь, которую можно выразить с помощью условной вероятности p_у(х) и условной энтропии Н_у(х). Обозначив через Н(х) и Н(у) соответственно энтропии на выходе объекта и измерительного устройства, можно показать, что с учетом статистической связи количество информации будет определяться известной формулой

 

.

 

В случае дискретных измерений это соотношение приводится к виду:

,

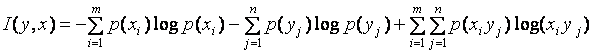где .

 

Количество информации, воспринимаемое измерительным устройством при непрерывном процессе, оценивается формулами получаемыми с помощью предельного перехода приведенных соотношений. В виду громоздкости формулы не приводятся.

 

Вопрос 32. Информация при равновероятных наблюдениях

 

3.4. Информация при равновероятных измерениях

 

На практике, как правило, имеют дело с равновероятными измерениями. В этом случае формулы, описывающие количество информации, значительно упрощаются:

 

I(y) = – log p,

 

где p – вероятность выбора одного из N сообщений (p=1/N).

В качестве примера рассмотрим физическую величину y (температуру, напряжение, давление и т.д.), изменяющуюся в пределах от у_maх до у_min. Обозначим за y_d = y_max – y_min.

Измерительное устройство остается нечувствительным к измерению в приделах приращения Dу. Поэтому даже при непрерывном изменении х можно получить некоторое число дискретных значений величины у,

равное .

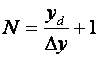Например, если отсчет производится от 0 до 1 В, то минимальное приращение, которое чувствует прибор, равно 0,01 В  и максимальное количество отсчетов будет равно 101.

Максимальную ошибку Dy принято называть разрешающей способностью прибора. Предположим, что минимальная относительная ошибка Dy/y_d не должна превышать ±e. Тогда требуемая разрешающая способность будет определяться величиной Dy=2e y_d.

Рассмотрим переменную, изменяющуюся со скоростью, равной 0,01 от полного диапазона изменения в секунду. Предположим, что мы можем  измерять переменную в статическом режиме с точностью до 1 %. Если отсчет может быть произведен быстро, то во время отсчета переменная может измениться лишь очень незначительно, а именно:

 

0,01 ´ 0,001 у_d = 0,00001 y_d.

 

Наоборот, если для отсчета требуется значительный промежуток времени, например 10 с, то переменная может измениться на 0,1у_d. Другими словами, чем быстрее изменяется переменная, тем больше потеря точности в течение интервала измерения. Промежуток времени T_r, необходимый для того, чтобы переменная изменилась на величину Dy, определится формулой:

 

.

 

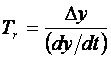Наименьший промежуток времени, необходимый для отсчета,

 

.

 

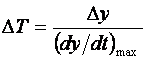С учетом полученных соотношений

 

 .

 

 При условии, если мы не располагаем никакими предварительными сведениями и каждый из N возможных отсчетов имеет одинаковую вероятность, искомое количество информации при измерении физической величины

.

 

В динамическом режиме, когда переменная изменяется на заметную величину за время DТ, максимальная скорость изменения информации, которая может регистрироваться измерителями,

 

.

 

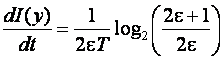Проанализируем варианты дискретных и непрерывных измерений. Пусть прибор производит 1000 измерений в секунду, каждое из которых дает 7 единиц информации (разрядов). Следовательно, скорость измерения информации равна 7000 ед./с.

Прибор непрерывного действия, имеющий время прохождения всей шкалы, равное 0,01с, и ошибку измерения e=0,045 (DТ=2´0,045´0,01=0,0009 с.) может измерить информацию со скоростью

.

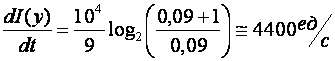Как видно из примера, у дискретного прибора количество информации в единицу времени значительно выше.

 

 

Вопрос 33. Смысловая мощность

 

5.4. Оценка смысловой мощности

 

Для сопоставления интеллектуальных возможностей объектов,  содержащих информационные системы, можно воспользоваться их информационным напряжением, т.е. их возможностью целенаправленно изменять вероятность того или иного события. Однако объективность такой оценки может быть достигнута только при равенстве информационных токов генерируемых  сравниваемыми объектами. Поэтому более эффективной оценкой является произведение информационного тока и напряжения – мощности:

 

,

 

где N – смысловая мощность (бит²/с).

Смысловой мощностью можно характеризовать не только источники, но и приемники информации. Если трактовать смысловую мощность как вырабатываемый, так и рассеиваемый в единицу времени  смысл соответствующей деятельности, понимаемый как мера интеллектуального труда, произведенного за время Т, можно записать:

 

 .

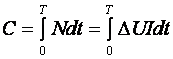Если DU=const, то

 

 .

 

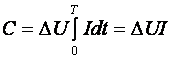Для примера определим смысловую мощность и интеллектуальный труд, вложенный оператором компьютера при наборе русского текста. Поскольку вероятности появления различных букв неодинаковы, можно для оценки информационного напряжения воспользоваться Шеннонской энтропией:

.

 

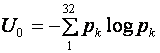Из расчетов, приведенных в параграфе 3.5, известно что U₀=4,35 бит. Полагая для простоты p_усл=1, т.е. оператор работает без ошибок, получаемое информационное напряжение

 

DU @ 4,35 бит .

 

Если оператор набирает текст со скоростью 300 знаков/мин, то информационная нагрузка, т.е. время набора одного знака, составляет t=0,2 сек. Таким образом, смысловая мощность оператора

 

 ,

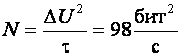а информационный ток

 .

 

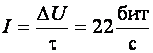Следовательно, за шести часовой рабочий день оператор вложит в свою работу умственного труда

 

С  =6´3600N = 2 ´10⁶ бит

и переработает информацию

 

I_р= 6´3600 I = 4,76 ´10⁵ бит.

 

 

Вопрос 34. Сигналы как материальные носители информации

 

5 Сигналы и их математические модели

 

5.1. Математические модели сигналов

 

В системах измерения и передачи информации в качестве сигналов используются различные физические процессы, характерезующиеся большим числом параметров. С точки зрения передачи информации существенны не все параметры. При использовании в качестве сигнала того или иного физического процесса выделяются  лишь некоторые его параметры. Приближенное представление физического процесса, используемого для передачи информации, можно назвать моделью сигнала.  

Параметры сигнала в общем случае можно разделить на структурные, идентифицирующие и информативные.

Для иллюстрации особенностей параметров сигналов различных типов рассмотрит пример.

Пусть математическое описание сигналов задается выражением:

 

и возможное сообщение содержится в значении амплитуды X синусоидального колебания. Величину X следует рассматривать как информативный параметр сигнала

По частоте f сигнала S обычно его выполняют среди других силналов того же класса  с другими значениями частоты. Таким образом, параметр f сигнала S можно отнести идентифицирующим параметром.

Число степенной свободы по информативному параметру сигнала в общем случае   зависит от t , по этому  параметр t (время) следует рассматривать как структурный  параметр  сигнала.

Информативный  параметр X может не зависить от структурного параметра t, например, когда выбранное значение амплитуды хÎX в соответствии с некоторым сообщением аÎA источника  информащия остается неизменным на всем протяжении сигнала. Поскольку с любым выражением значением амплитуды x при этом всегда связана  гармоническая составляющая sin(2pf +j), то рассмотренный вариант кодировки сообщений Q: А®Х эквивалентен правилу Q’: А®S, где, , т.е. каждое возможное сообщение сопоставляется с гармоническим колебанием бесконечной длительности и определенной амплитуды. Итак, в рассмотреном варианте сигнал S по информативному параметру X имеет лишь одну степень свободы.

Если амплитуда Х зависит от париметра t, то возможные сообщения можно сопоставить со значениями сигнала в различные моменты времени. Пусть, например, возможные сообщения сопоставляются на отрезке времени Т значениям информативного парметра Х (t) сигнала в моменты времени t₁, t₂, …., t_n  отстоящие друг от друга на интервалы, равные Dt. Тогда сигнал S(t) на отрезке времени Т будет содержать     компонентов, равное числу степеней свободы сигнала. Структурный параметр t в рассматриваемом примере играет роль индексирующего параметра и может быть заменен некоторым подмножеством натуральных чисел. Причем, если параметр t принимает счетное множество, то сигнал S(t) в принципе имеет бесконечное число степеней свободы.

В качестве информативных могут использоваться различные параметры. Так, например, в нашей модели информативных могут использоваться параметры Х, f, j, причем частота f может одновременно быть и информативным, и идентифицирующим параметром.

Сигналы, как сообщение, по своим информативным параметром  разделяются дискретные и непрерывные. Если множество возможных значений информативного параметра сигнала конечно или счетно, то сигнал называется дискретным по данному параметру. Если информативный параметр сигнала принимает континуум значений, то сигнал называется непрерывным по данному параметру. Если информативный параметр не один, то сигнал может быть дискретным по одному и непрерывным по другому параметру.

Иногда бывает удобно пользоваться понятием «состояние сигнала», которое определяется тем, какие конкретные значения примут и информативные параметры по каждой степени свободы. В общем случае число возможных состояний сигнала определяется выражением:

где m_i – число возможных значений i-го параметра сигнала

n – число степени свободы сигнала.

Очевидно, что если число степени свободы сигнала или по крайней мере один из сомножителей бесконечно большой, то и число состояний сигнала будет бесконечно большим. Так как при передачи данных происходит изменение значений информативных параметров сигнала и, следовательно, изменение состояния сигнала в соответствие с передаваемыми сообщениями, то информация, переносимая сигналом, заключается именно в его соответствии.

В некоторых случаях для упрощения математической модели при описание сигналов отвлекаются от идентифицирующих параметров и связаных с этими параметрами составляющих сигнал. В частности, математической моделью сигнала может служить случайный процесс, дискретный или непрерывный. В случае дискретного мы имеем конечную или бесконечную последовательность X₁, X₂, X₃…, X_i, …, X_n случайных величин, возможное значение которых сопоставляются с возможными сообщениями. Число степеней свободы такого сигнала определяется верхней границей n структурного параметра i. При n=1 мы имеем дело с сигналом, математическая модель которого совпадает с математическим описанием соответствующей случайной величиной. При конечном n математическая модель сигнала, в частности, может быть полностью задана n-мерным законом распределения системы случайных величин X₁, X₂, X₃, …, X_n.  При n®¥ полное описание случайного процесса конечномерными законами распределения не везде возможно. Однако, учитывая особенности реальных исчточников информации, бесконечные последовательности случайных величин обычно представляют в виде простых цепей Маркова, что упрощает соответствующее описание дискретного случайного процесса.

Другой разновидностью математических моделей сигнала может служить непрерывный случайный процесс X_t, структурный пример которого tÎT принимает континуум значений. Математическое описание непрерывного случайного процесса в значительной степени зависит от ограничений на него.

Для того, чтобы с помощью математической модели сигнала оценивать помехоустойчивость, в ней должна быть определена степень различия мехду возможными состояниями сигнала, Одним из приемов является представление возможных состояний сигнала в виде точек в некотором абстрактном пространстве, в котором тем или иным способом определено расстояние между двумя точками. В таких пространствах степень различия возможных состояний сигнала выражается расстоянием между точками, соответствующими этим состояниям.

В аналитической геометрии трехмерное пространство отожествляется с тройкой вещественных чисел (x, y, z). Эта тройка вещественных чисел с введенными определенным образом понятием расстояния между двумя точками (x_1, y_1, z₁) и (x_2, y_2, z₂) может служить моделью пространства. Представление пространства в форме последовательности действительных чисел, интерпритируемых как независимые координаты, позволяет обобщить понятие пространства, Так, например, под четверкой действительных чисел (x_1, x_2, x_3, x₄) можно понимать четырехмерное пространствои вообще под последовательностью из n действительных чисел (x_1, x₂ …x_n) понимать n-мерние пространство.

И так, учитывая вероятностную природу сигнала, состояние которого изменяется случайным образом, под математической моделью сигнала общем случае будет понимать абстрактное пространство с заданной на нем вероятностней лучей, элементами которого являются возможные состояния сигнала ( в частности, значения информативного параметра) и в каждом определено расстояние между любыми двумя элементами.

 

Вопрос 35. Энтропия непрерывных сигналов

 

6.3 Энтропия непрерывных сигналов

 

Отметим, что непрерывным называется сигнал, у которого множество значений информативного  параметра эквивалентно множеству действительных чисел.

Представим непрерывный сигнал с одной степенью свободы в виде непрерывной случайной величины X, плотность распределение которой равна f(x). Разобьем область значения случайной величины X на малые интервалы Dx, примыкающие друг к другу. Число таких интервалов конечно (или счетно). Вероятность попадания случайной величины X в некоторый i-й интервал приблизительно равно произведению плотности распределения в точке, соответствующей одной из границ i-го интервала, на этот интервал. После такой дискретизации непрерывной случайной величины X можно записать выражение для оценки случайной величины X в виде

 

 

Значение энтропии, вычисленное по этой формуле, тем точнее, чем меньшими выбраны интервалы дискретизации Dx. В пределе при Dx®0 получим:

 

 

Анализируя полученное выражение, приходим к выводу, что энтропия непрерывного сигнала X стремится к бесконечности при неограниченном уменьшении величины Dx.

На первый взгляд полученный результат может показаться весьма обнадеживающим: если энтропия сигнала неограниченно велика, значит с помощью него можно предать неограниченное количестве информации. Для этого достаточно лишь полностью снять неопределенность, которую он априорно заключает в своем состоянии. Но что значит полностью снять неопределенность? Это значит получить более точный отсчет значений принятого сигнала. Но в реальных условиях это осуществить невозможно. Непрерывный сигнал всегда воспринимается приближенно, с ограниченной точностью. Поэтому в последние выражение величине Dx вполне логично  придать смысл некоторого интервала неопределенности, которым, например, характеризуется система, воспринимающая сигнал, или же шага квантования возможный значений сигнала, т.е. так или иначе можно считать величину Dx конечной. В этом случае энтропия непрерывного случайного сигнала необязательно должна стремиться бесконечности и при достаточно малых интервалах Dx выражение для энтропии непрерывного сигнала принимает вид:

или

К аналогичному результату можно прийти, с определять энтропию сигнала X относительно другого сигнала Y с некоторым стандартным распределением f(y) его значений как разность  энтропий сигналов X и Y. Полученную таким способом энтропию сигнала X называется относительной энтропией. Обычно в качестве стандартного выбирается равномерное распределение

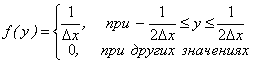
Предельный переход с помощью квантования значений сигналов X и Y с шагом e и последующим устремлением e к нулю позволяет получить выражение для относительной энтропии, аналогичное выражению для H_Dx(x).

Индекс Dx в обозначении энтропии напоминает о том, что значение энтропии непрерывного сигнала связанно с интервалом неопределенности Dx, выбранного исходя из тех или иных соображений в зависимости от реальных условий, в который действует сигнал.

Вводя обозначения

,

можно записать выражение для H_Dx(x) в виде

Первый член этой разницы называется приведенной энтропией и полностью определяется статистикой значений сигнала X, и этой составляющей во многом определяются свойства энтропии сигнала. Второй член, напротив, зависит лишь от интервала неопределенности  Dx, и можно легко проследить влияние его на энтропию сигнала: при увеличении или уменьшении величины Dx энтропия соответственно или убывает или возрастает.