Вопрос 26. Линейные коды

6.14. Линейные коды

Общий (N,M) код с проверками на четность может быть задан с помощью k = N-M равенств вида:

(*)

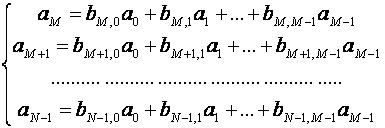Все коэффициенты b_M_,₀_, b_M_,1, …, b_M_,_M_–₁_, …, b_N_–_1,0, b_N_–_1,1, …, b_N_–₁_,_M_–₁– это элементы поля из двух элементов (чисел 0 и 1), а все входящие в эти равенства арифметические действия понимаются в смысле двоичной арифметики (каждое равенство означает, что его левая и правая части имеют одинаковую четность). Напомним: 0+0=0, 0+1=1, 1+0=1, 1+1=0.

Таким образом, проверки на четность, отвечающие N,M – коду, – это проверки на четность суммы контрольного сигнала a_i и тех информационных сигналов a₀, a₁, a₂_,
…,a_M_–₁, которым соответствуют равные единице коэффициенты b_i_,₀, b_i_,₁, b_i_,2,_…,b_i_,_M_–1.

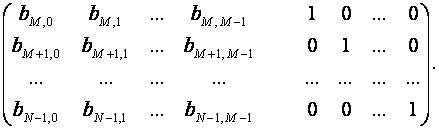Для задания кода достаточно указать все коэффициенты b_i_,_j, входящие в выписанные равенства. Обычно левые части a₀, a₁, a₂_,
…,a_M_–₁ переносят направо. Так как в двоичной арифметике –1 = 1, то знаки при переносе не изменяются. Поэтому полученная система уравнений приводится к виду

Полученная матрица В имеет k строк и N столбцов. На пересечении i–ой строки и j–го столбца находится коэффициент при а_j. Таким образом, общий N,M – код с проверками на четность задается матрицей из нулей и единиц. Совокупность всевозможных кодовых обозначений общего

N,M–кода с проверками на четность может быть описана следующим образом:

- информационные сигналы a₀, a₁, a₂_{, …,}a_M_–₁ могут быть любыми;

- контрольные сигналы a_М, a_М+₁, a_М+₂_{, …,}a_N_–₁определяются информационными с помощью полученных выше равенств;

- общее число кодовых обозначений 2^М = 2^N^–^k .

Если а = a₀, a₁, a₂_,
…,a_N_–₁ - вектор–столбец, то равенство В´ а=0 отразит суть проверки на четность, где В принимает значения проверяющей матрицы.

Вопрос 27. Декодирование с проверками на четность

6.15. Декодирование с проверкой на четность

Обозначим отдельные столбцы проверочной матрицы В через

В = (b₀_, b₁_, …, b_M_–₁, b_М, b_М+_1, …, b_N_–₁).

Пусть е = е₀, е₁, е_{2, …,}е_N – N-членный блок ошибок, содержащий единицы в местах тех элементарных сигналов передаваемого кодового обозначения, которые исказились при передаче. Следовательно, В´ е = S, где

S = (e₀b₀_, e₁b₁_, …, e_M_–₁ b_M_–₁, e_M b_М, e_M₊₁ b_М+_1, …, e_N_–₁ b_N_–₁) .

Таким образом, блок S, который получается при подстановке в систему уравнений (*) вместо передаваемых сигналов a₀, a₁, a_2,_…,a_N_–₁ принятые сигналы a'₀, a'₁, a'₂_,
…,a'_N_–₁, на основании которого мы можем судить об имеющихся ошибках, равен сумме столбцов проверочной матрицы В, искаженных при передаче, то есть е_i = 1.

Остальным сигналам соответствуют значения е_i = 0. Отсюда видно, что одиночным ошибкам соответствуют блоки S, содержащие одну единицу и совпадающие со столбцами b_i проверочной матрицы В. Отсутствие ошибок определяет блок S = 0. Поэтому для того, чтобы код с проверками на четность позволил различать случаи отсутствия ошибок и все одиночные ошибки, необходимо, чтобы все столбцы соответствующей матрицы В были различными и ни один из них не был нулевым.

В случае двоичной симметричной линии общее количество

k–значных блоков b = b_М, b_М+₁_, …, b_N_–₁ должно быть равно числу целых чисел, записанных в двоичной системе исчисления 2^k. Так как из числа возможных столбцов матрицы В исключается нулевой блок (0, 0, 0, …., 0), то число различных столбцов оказывается равным 2^k–1. Следовательно,

код с проверками на четность, исправляющий все одиночные ошибки и содержащий k контрольных сигналов, должен состоять из кодовых обозначений, длина которых не превосходит 2^k–1.

Например, при k = 4, N = 2⁴ –1 = 15. Соответствующая (4´15) матрица В будет иметь вид

При такой записи В роль контрольных сигналов будут играть первый, второй, четвертый и восьмой столбцы. Они состоят из трех нулей и одной единицы. Остальные 11 столбцов будут относиться к информационным сигналам.

Блок S будет нулевым в случае отсутствия ошибок при передаче, а в случае одной ошибки он будет равен соответствующему столбцу В, то есть будет непосредственно задавать двоичную запись того сигнала, который исказила передача.

Аналогично строятся коды, исправляющие две и более ошибок.

Вопрос 28. Информационные цепи

5. Источники и потребители информации

5.1. Информационные цепи

Теория информации располагает достаточно широким спектром прикладных задач. Первоначальная ориентация на проблемы передачи данных и теорию связи, к настоящему времени трансформировалась в создание собственного прикладного направления – информационных технологий. Информационные технологии объединяют проблемы сбора, обработки, передачи и хранения информации. И сейчас трудно найти

область человеческой деятельности, где эти проблемы не были бы актуальны.

Рассмотрим некоторые инженерные методы построения информационных цепей. Под информационной цепью понимают совокупность взаимодействующих источников, преобразователей и потребителей информации. В общем случае информационные цепи представляют собой сложные сильно разветвленные многоканальные иерархические структуры. Однако в простейшем случае элементарная информационная цепь состоит из одного источника информации и одного потребителя информации, а также связывающих их информационных каналов (линий связи). Информационные цепи обычно замкнуты на источник посредством прямой и обратной связи (рис. 7).

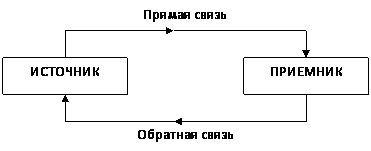Рис. 7. Структура информационной цепи

Воспользуемся понятием неопределенности окружающей нас среды. В этом случае в предположении равновероятности наступления события p₀ введем понятие информационного потенциала некоторого события:

U₀ = – log p₀.

Предположим, что наша информационная цепь предназначена для задач управления. Целью и смыслом всякого управления является изменение в ту или иную сторону априорной вероятности p₀ до некоторого нового значения p_усл, которому соответствует новое значение потенциала U_усл = – log p_усл., где p_усл –вероятность события при наличии управления.

Таким образом, сущность управления, осуществляемого источником информации, может характеризоваться информационным напряжением:

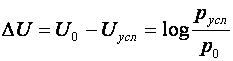Например, оператор, управляющий прокатным станом, является источником информации по отношению к системе управления прокатного стана. Его информационное напряжение равно логарифму отношения вероятности успешной работы стана с оператором к вероятности успешной работы стана без оператора.

Рассмотрим количественный пример подсчета информационного напряжения. К объекту, обороняемому ракетно-зенитной установкой, сквозь внешнее оборонительное кольцо прорвались два однотипных самолета противника, один из которых расстрелял свой разрушительный боезапас в процессе прорыва. Предположим, что зенитная установка имеет возможность поразить оба самолета с вероятностью 0,5.

Если будет использована система оповещения, то она правильно направит установку на опасный самолет, и он будет уничтожен с вероятностью 1. Требуется определить информационное напряжение системы оповещения. Оно определяется таким образом:

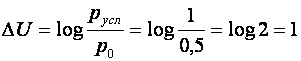бит.

5.2. Электротехнические аналогии в информационных цепях

Если информационное напряжение в цепи характеризует источник информации, то по аналогии с электрическими цепями можно охарактеризовать приемник информации подобием сопротивления. Информационное сопротивление определяется временем реакции нагрузки на полученную информацию (время исполнения), которое исчисляется с момента выхода информации из источника до момента получения источником сигнала обратной связи о достижении поставленной цели. Если ввести понятие информационного тока I, характеризующего интенсивность передачи информации по линиям связи, то можно прийти к понятию информационного закона Ома:

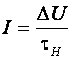где t_Н – информационное сопротивление приемника.

Очевидно, что при работе информационной цепи в течение времени T в ней будет протекать информация

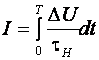Вопрос 29. Последовательное соединение источников информации

Последовательное соединение элементов цепи

При последовательном соединении (рис. 8) через источник и нагрузку протекает один и тот же информационный ток I.

Рис .8. Последовательное соединение:

ИДЛ – информационно-движущая логика

Естественно, что напряжение двух источников информации ИДЛ 1 и ИДЛ 2 будет равна сумме их напряжений:

Очевидно, что при последовательном соединении источников информации увеличивается вероятность достижения желаемого события, так как:

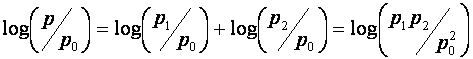где p₁< p₁p₂/> p_2.

Вместе с тем последовательное соединение источников приводит к увеличению их суммарного внутреннего сопротивления:

поэтому оно эффективно только в том случае, если случайная задержка решения в источниках информации значительно меньше информационного сопротивления нагрузки.

Вопрос 30. Параллельное соединение источников информации

Параллельное соединение

При параллельном соединении источники работают с одинаковым напряжением DU, а в нагрузку поступает их суммарный информационный ток I = I₁ + I₂ (рис. 9, а).

На рис. 9 б, в представлены схемы соединения нагрузок в информационной цепи.

Особенностями информационных цепей являются временные последовательности поступления информации в нагрузки, что характерно для схем с временной селекцией.

О последовательном соединении нагрузки можно говорить в том случае, когда информация сначала поступает в первую нагрузку и лишь после отработки управляющей информации – во вторую:

В случае параллельного соединения нагрузок (рис. 9, в) имеет место наличие нескольких исполнительных органов, каждый из которых самостоятельно достигает поставленную цель. Следовательно;

В качестве параллельных основной нагрузке могут выступать посторонние нагрузки, создающие утечки информации. В такой роли нередко оказываются всевозможные контролирующие органы, которые нередко настолько перегружают источник требованием отчетов, что он снижает свое напряжение, т.е. снижается вероятность достижения своей прямой цели, поскольку он не в состоянии обеспечить информацией объект управления.

а)

б)

в)

Рис. 9. Схемы соединения элементов информационной цепи: а - параллельное соединение источников; б - последовательное соединение нагрузок;

в - параллельное соединение нагрузок