Вопрос 21. m-ичная линия связи

6.9. М–ичная симметричная линия

Пусть по линии связи передается m различных элементарных сигналов А₁, А₂, …, А_m_, причем, те же сигналы принимаются на приемном конце линии с вероятностью безошибочной передачи 1–р. В случае ошибки передаваемый сигнал с одинаковой вероятностью р/(m–1) может быть воспринят как любой из m–1 отличных от него сигналов.

Математическая модель такой линии может быть представлена матрицей

Соответствующая этой модели линия связи называется m–ичной симметричной линией.

Учитывая, что I(a, b) = H (b) – H_a(b), а условные энтропии

Н_А₁(b) = Н_А₂(b) = ……= Н_А_m(b) = – (1–р) log (1–p) –

- (m–1) р / (m–1) log р / (m–1),

то H_a(b) = – (1–р) log (1–p) – p log р / (m–1) .

Условная энтропия H_a(b) не зависит от вероятностей р,

р(А₁), р(А₂), р(А₃), …, р(А_m)

и для нахождения пропускной способности C необходимо лишь определить наибольшее значение H (b). Оно достигается при равновероятном значении сигналов, то есть для этого необходимо, чтобы вероятности посылок сигналов р(А₁), р(А₂), р(А₃), …, р(А_m) были равны.

Поэтому

р⁰(А₁) = р⁰(А₂) = р⁰(А₃) = … = р⁰(А_m) = 1/m.

c = I(a, b) = log m + p log p / (m–1) + (1–p) log (1–p)

и C = L [log m + p log р / (m–1) + (1–p) log (1–p)] .

Для m = 4 график функции С(р) изображен на рис. 15.

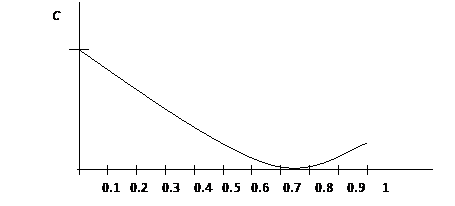
Рис. 15. Пропускная способность m-ичной линии (m=4)

Максимум функции С(р) достигается при отсутствии помех. При р = р/(m–1) пропускная способность линии будет равна нулю. При дальнейшем увеличении р наблюдается небольшое увеличение С, так как, приняв сигнал А_i, мы можем сделать вывод о том, что более вероятной является посылка сигнала отличного от А_i.

Вопрос 22. Коды, обнаруживающие и исправляющие ошибки

6.10. Коды, обнаруживающие и исправляющие ошибки

Основной проблемой теории кодирования является проблема отыскания таких методов кодирования, которые бы обеспечивали достаточно высокую скорость передачи и, одновременно, малую вероятность ошибки. Наиболее существенно здесь требование, чтобы и кодирование и декодирование можно было бы достаточно просто осуществлять на практике. Удовлетворять последнему требованию довольно нелегко и этому посвящены основные исследования самостоятельной теории – теории кодирования.

Ограничимся рассмотрением двоичных линий связи, то есть будем считать, что по линии связи передаются два элементарных сигнала, которые обозначаются цифрами 0 и 1. В настоящее время такие линии наиболее широко распространены и их чаще всего называют цифровыми. В этом случае все кодовые обозначения будут последовательностями этих цифр, то есть числами, записанными в двоичной системе исчисления. Как было отмечено ранее, кодовое обозначение длины N здесь можно выбирать из числа 2^Nразличных N–значных двоичных чисел – последовательностей:

а₀, а₁, а₂, а₃, ……, а_N_–₁,

где все а_i (i = 0,1, 2, 3, ……, N–1) принимают значения 0 или 1.

Если 2^Nразличных N–значных числа мы примем за кодовые обозначения, то скорость передачи информации будет наибольшей, но зато при этом у нас не будет никакой возможности определить на приемном конце линии связи, имелись ли ошибки при передаче, сколько их было и какие именно сигналы приняты неправильно. Если мы ограничимся меньшим числом кодовых обозначений, то возникающая при этом "избыточность" кода может быть использована для дополнительной передачи некоторых сведений об искажениях, внесенных линией связи. Так, например, можно воспользоваться N–кратным повторением каждого элементарного сигнала. В этом случае в качестве кода применяют два обозначения 000…0 и 111…1 длины N, а на приемном конце линии расшифровывают принятую цепочку длины N как 0, если в ней больше нулей, и как 1 – в противном случае. Очевидно, что такой метод передачи при достаточно большом N обеспечит очень малую вероятность ошибки при расшифровке передаваемого сигнала, но скорость передачи будет мала.

Сравнительно общий прием использования избыточности в кодовых обозначениях при передаче информации об искажениях может быть пояснен следующим примером. Условимся сопоставлять 2^N^–1кодовых обозначения всевозможным цепочкам а₀, а₁, а₂, а₃, ……, а_N_–₂ из N–1 цифр, а N–ую цифру а_N_–₁ будем каждый раз выбирать так, чтобы сумма а₀ + а₁ + а₂ + а₃ + …+ а_N_–₁_, была четной. В этом случае наличие одиночной ошибки приведет к появлению на приемном конце линии связи такой цепочки а'₀, а'₁, а'₂, а'₃, ……, а'_N_–₁, что сумма а₀ + а₁ + а₂ + а₃ + …… + а_N_–₁, будет нечетной (искажения заключаются в том, что 0 будет принят за 1, а 1 за 0).

Это обстоятельство позволяет легко обнаружить наличие одиночной ошибки, хотя и не позволяет выяснить, какой сигнал был принят неверно. Тем не менее, в тех случаях, когда вероятность появления более одной ошибки достаточно мала, описанный метод представляет собой достаточно большую ценность. Если мы наверняка знаем, что прием сопровождался ошибкой, то можно просто проигнорировать полученное сообщение или повторить передачу.

Вопрос 23. Кодирование с проверкой на четность

6.11. Кодирование с проверкой на четность

Описанный прием можно также применить несколько раз и это уже позволит не только обнаружить наличие ошибок, но и исправить их. Например, при N = 3 мы будем использовать два кодовых обозначения. В этом случае разумно выбирать тройки 000 и 111. Сопоставим два кодовых обозначения двум возможным значениям первого элемента а_0, а далее условимся вслед за каждым "информационным" сигналом передавать еще два "контрольных" сигнала а₁ и а₂ подобранных так, чтобы обе суммы а₀+а₁и а₀+а₂были четными. В таком случае легко видеть, что если при приеме тройки сигналов не произошло сразу двух или трех ошибок, то, проверив нечетность сумм а'₀+а'₁и а'₀+а'₂в принятой на приемном конце тройки а'_0, а'₁и а'_{2 ,} можно безошибочно установить, какая же именно тройка была на самом деле передана. Если обе суммы а'₀+а'₁и а'₀+а'₂ окажутся четными, то это значит, что ошибок при передаче не было. Если нечетной будет лишь одна из них, то это означает, что ошибочно принят входящий в сумму контрольный сигнал а₁ или а₂, а если обе суммы а'₀+а'₁и а'₀+а'₂ – нечетные, то следует признать ошибку информационного сигнала а₀.

Таким образом, ценой уменьшения скорости передачи можно добиться того, чтобы все одиночные ошибки были исправлены.

Если N = 7, а число кодовых обозначений 16, то можно принять за информационные сигналы первые 4 сигнала (так как число различных четверок а₀, а₁, а₂, а₃равно 16, то есть 2⁴), а последние три контрольных сигнала а₄, а₅, а₆ чтобы были четными суммами:

S₁= а₀+ а₁+ а₂ + а₄ ;

S₂= а₀+ а₁+ а₃ + а₅ ;

S₃= а₀+ а₂+ а₃ + а₆ .

Проверка на четность трех сумм S₁, S₂, S₃на приемном конце линии лишь позволяет однозначно установить, была ли допущена ошибка при приеме, и если была, то в чем она заключается:

– если один из семи сигналов будет принят неверно, то одна из сумм окажется нечетной. При одной нечетной сумме ошибка будет в одном из трех контрольных сигналов;

– нечетность двух из трех сумм будет означать, что неверно принят тот из трех сигналов а₁, а₂ , а₃ , который входит в обе эти суммы;

– нечетность всех трех сумм означает ошибку в сигнале а₀.

Нетрудно видеть, что 16 первых обозначений длины 7 имеют вид:

0000000 1000111 0100110 1100001

0010101 1010100 0110011 1110100

0001011 1001100 0101101 1101010

0011110 1011001 0111000 1111111

Вопрос 24. Соотношение контрольных и информационных сигналов

6.12. Соотношение контрольных и информационных сигналов

Описанные примеры кодов с проверками на четность, позволяющими исправить одну ошибку, перекликаются с задачами из занимательной математики на отыскание фальшивых монет и на угадывание чисел с наименьшим числом вопросов. Вместо n чисел рассмотрим N номеров 0, 1, 2, 3, …, N–1, входящих в кодовое обозначение

а₀, а₁, а₂, …, а_N_–₁.

Следовательно, для выяснения заданного числа требуется затратить не меньше, чем log (N+1), не больше, чем log (N+1)+1 вопросов.

Проверка на четность фактически эквивалентна вопросам, имеющим ответ "да" или "нет", а условие обязательной четности при правильном ответе дает возможность получения информации при ошибке. Отсюда следует, что число требуемых добавочных контрольных сигналов совпадает с числом вопросов. Если, например, N = 3, то число вопросов не может быть меньше чем log (3+1) = log 4 = 2. Это соответствует примеру кода, исправляющего одиночные ошибки. Каждый передаваемый информационный сигнал а₀ дополняется двумя добавочными контрольными сигналами а₁и а₂. Аналогично, если N = 7, то число требуемых вопросов и, соответственно, контрольных сигналов не может быть меньше, чем log (7+1) = log 8 = 3. В общем случае кодовых обозначений длины N число k контрольных сигналов кода, исправляющего все одиночные ошибки, должно удовлетворять неравенству

log (N+1) £ k £ log (N+1)+1 .

Число информационных сигналов равно N–k. Код, использующий кодовые обозначения длины N, состоящий из M = N–k информационных сигналов и k контрольных сигналов, используемых для проверки на четность, называется (N–M) – кодом.

Учитывая, что k £ log (N+1)+1, при больших N число k будет гораздо меньше N, скорость передачи будет близка к максимальной. Отсюда следует, что рассматриваемые коды при большом N будут обеспечивать более высокую скорость передачи. Однако очень большое N выбирать все же невозможно, так как при этом значительно увеличивается вероятность появления нескольких (более одной) ошибок в блоке из N сигналов.

Рассмотренный (7,4) код, исправляющий одиночные ошибки впервые был рассмотрен К. Шенноном. Общие (N,M) коды, исправляющие одиночные ошибки, разработаны в 1950 г. Р. Хеммингом и обычно называются кодами Хемминга.

Вопрос 25. Исправление нескольких ошибок

6.13. Исправление нескольких ошибок

Рассмотрим пример исправления нескольких ошибок при передаче информации. Допустим, что при N = 5 мы пренебрегаем одновременным искажением более двух сигналов из пяти. Потребуем, чтобы код позволил исправлять все искажения во всех случаях, когда их число не превосходит двух. Эти условия приводят нас к известной математической задаче об определении n£ 2 загаданных чисел. Количество вопросов, необходимых для угадывания этих чисел, определено выражением

log (C₅² + C₅¹ + 1) = log 16 = 4 вопроса.

Поэтому нам потребуется четыре проверки на четность. Следовательно, из каждых пяти сигналов а_0, а_1, а₂, а₃, а₄ по крайней мере четыре должны быть контрольными. Для данного примера можно выбрать суммы:

S₁ = a₀ + a₁;

S₂ = a₀ + a₂;

S₃ = a₀ + a₃;

S₃ = a₀ + a₄.

В этом случае - четность всех рассматриваемых сумм будет означать отсутствие ошибок;

- нечетность одной суммы S_i – ошибку в соответствующем сигнале a_i;

- нечетность двух сумм S_i и S_j – ошибки в сигналах a_i и a_j;

- нечетность трех сумм (допустим всех кроме S_i ) – ошибку в сигналах a₀ и a_i;

- нечетность всех четырех сумм – единственную ошибку в сигнале a₀ .

В более общем случае кодов, исправляющих одну или две ошибки в "блоках", из произвольного числа N сигналов можно показать число k контрольных сигналов и отвечающих им проверок на четность, которое не может быть меньшим чем

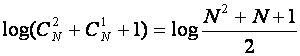В случае построения кодов, позволяющих обнаружить и исправить в цепочке сигналов длины N любое число ошибок, не превосходящее заданное n, число проверок на четность и соответствующее число k контрольных сигналов должно быть не меньше, чем

Неравенство называется неравенством Хемминга, а число k – нижней границей Хемминга для числа контрольных сигналов, исправляющих n ошибок. Если n = 1, неравенство Хемминга приводит к уже известному результату:

N £ 2^k –1 .

Но в любом случае полученные результаты не указывают, как выбирать необходимые нам проверки на четность. Более того, они не позволяют даже утверждать, что для любого k, удовлетворяющего неравенству Хемминга, действительно существует код с проверками на четность, содержащий k контрольных сигналов и позволяющий исправить любое меньшее чем n число ошибок в блоке из N сигналов.

Оценка числа k контрольных сигналов, заведомо достаточного для возможности обнаружить и исправить любое меньшее чем n число ошибок, была получена Р.Р.Варшамовым, показавшим, что при

всегда можно построить код с проверками на четность, обладающий необходимыми свойствами. Этот результат, уточняющий результат ранее полученный Э. Гилбертом, принято называть неравенством Варшамова – Гилберта.

Таким образом, существуют значения числа контрольных сигналов k, для которых соответствующие неравенства не исключают возможности для построения кода, исправляющего n ошибок.