Вопрос 16. Пропускная способность линии связи

 

6.4. Пропускная способность линий связи

         Роль энтропии в передаче сообщений определяется основным соотношением, ограничивающим максимальную скорость передачи элементов сообщения в единицу времени:

                                                                      ,

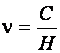где Н – энтропия одного элемента сообщения;

      С – пропускная способность линии связи,  .

Здесь L – число элементарных сигналов, которое можно передать по линии связи   в единицу времени;

         m – общее число используемых сигналов.

         На практике число m выбирается с учетом возможности построения приемо–передающей аппаратуры. В основном используются два элементарных сигнала (импульс и пауза). Для каждой линии существует минимальный промежуток времени t₀, который разделяет сигналы. Поэтому максимальное значение L = 1/t₀ и это число является основной технической характеристикой линии связи.

В работах В. Котельникова число L выражается через ширину полосы пропускания. В случае радиосвязи перестройка линий с целью увеличения L не может принести выгоды, поскольку она сделает невозможной работу радиолиний, ведущих передачу на близких частотах.

         Проанализируем возможности изменения m для увеличения пропускной способности линии связи. Известно, что во время передачи информации на линию связи действуют различного рода помехи. Если обозначить за W среднюю мощность помех, то те сигналы, которые будут иметь мощность меньшую, чем W мы не сможем выделить на приемном конце линии. Поэтому различимыми будут лишь те сигналы, которые отличаются не меньше, чем на определенное значение. Уровень передаваемых сигналов (со средней мощностью Р) не может быть безгранично велик и может существовать только конечное число градаций сигнала m. Количественный анализ соотношения мощности сигнала и помехи был приведен К. Шенноном. Он показал, что

 .

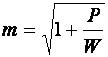         Таким образом, пропускная способность линии связи определяется

.

 

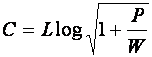Вопрос 17. Передача информации при наличии помех

 

6.5. Передача информации при наличии помех

 

Процесс передачи сообщений по линии связи в условиях действия помех можно пояснить схемой (рис.12).

 

 

 

 

 

                                                

 

                                                     

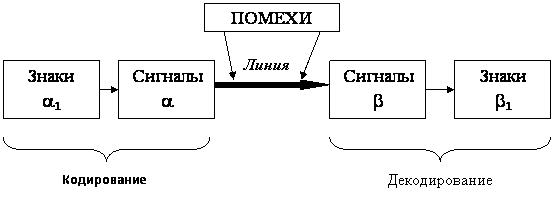
Рис. 12. Схема реальной линии связи

 

         В случае передачи текстовых сообщений a₁ и b₁, они записываются на определенном языке с помощью буквенного алфавита и могут отличаться друг от друга в результате действия помех. Сигналы a и b на входе и выходе линии связи представляют собой последовательности электрических сигналов. Операции кодирования и декодирования состоят в преобразовании буквенного сообщения  a₁ в последовательность элементарных сигналов a и в обратном преобразовании сигналов b в буквенное сообщение b₁. Ранее мы рассматривали линии связи без учета влияния помех. Проанализируем теоретические подходы к учету влияния помех. Для простоты примем допущения о взаимной независимости букв сообщения, причем n букв алфавита характеризуются вероятностями р₁, р₂, …, р_n. В линии связи используется m различных элементарных сигналов А₁, А₂, …, А_m, причем за единицу времени может быть передано L таких сигналов. Как было отмечено ранее, при отсутствии помех сообщение может быть передано со скоростью сколь угодно близкой к

  ,

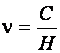где C = L log m ;

      Н – энтропия, приходящаяся на одну букву сообщения,

.

         Для достижения скорости передачи, близкой к n, необходимо разбить передаваемое сообщение на достаточно длинные блоки и передавать его кодом близким к оптимальному, например, кодом Шеннона-Фано. Иначе говоря, для этого необходимо воспользоваться кодом, для которого избыточность в закодированном сообщении была бы минимальной.

         При наличии помех в линии связи именно избыточность в передаваемой последовательности сигналов может помочь точно восстановить переданное сообщение по принятым данным. В случае значительных помех еще более увеличивается избыточность, например, проверяя каждое переданное слово по несколько раз или заменяя каждую букву сообщения отдельным словом, начинающимся с этой буквы. Очевидно, что в этом случае скорость передачи данных уменьшается.

 

 

 

Вопрос 18. Потери информации при передаче

 

6.6. Потери информации при передаче

 

         Предположим, что рассматриваемая линия связи использует m различных элементарных сигналов А₁, А₂, …, А_m, но из–за наличия помех передаваемый сигнал А_i (где i = 1,2,3, …, m) может быть иногда принят на приемном конце линии за другой сигнал А_j. Зададим вероятность р_А1(А₁) того, что передавая сигнал А₁, на приемном конце получим сигнал без искажения, то есть А₁. Обозначим за вероятности типа р_А1(А₁) – вероятности безошибочной передачи. Вероятности р_А1(А₂), р_А1(А₃), …, р_А1(А_m) того, что переданный сигнал А₁ будет на приемном конце расшифрован, как А₂, А₃, …, А_m. Далее задаются вероятности р_А2(А₁), р_А2(А₂), р_А2(А₃), …, р_А2(А_m) получения на приемном конце сигналов А₁, А₂, А₃,  …, А_m.

         В результате можно получить математическую характеристику линии связи в виде:

 

 

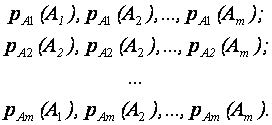
         Вероятности безошибочной передачи сигналов по линии связи располагаются по диагонали матрицы.

Приведенное описание линии связи с помехами можно несколько обобщить, допустив, что  помехи могут иногда так исказить передаваемый сигнал, что на приемном конце его нельзя будет отождествить ни с одним из m используемых сигналов А_j. Для того, чтобы учесть такую возможность, целесообразно допустить, что на приемном конце могут быть получены не обязательно те же m элементарных сигналов А₁, А₂, …, А_m, а совсем другие r элементарные сигналы: В₁, В₂, …, В_r. В этом случае помехи будут статистически характеризоваться mr неотрицательными числами:

 

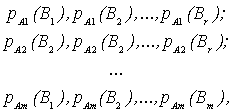
удовлетворяющими m условиям

 

p_Аi(В₁) + p_Аi(В₂) + p_Аi(В₃) + … + p_Аi(В_r) = 1,  при i = 1, 2, 3, …, m,

 

где р_Аi(B_j) – вероятность того, что на приемном конце будет принят сигнал В_j, если на самом деле был передан сигнал А_i.

         Предположим, что р(А₁) – вероятность того, что передаваемым сигналом является А₁; р(А₂) – вероятность сигнала А₂, …; р(А_m) – вероятность сигнала А_m (р(А₁) + р(А₂) + …. + р(А_m) = 1). В таком случае опыт b, состоящий в определении того, что именно такой сигнал передается, будет иметь энтропию

Н (b) = – р(A₁) log p(A₁) – р(A₂) log p(A₂) –…– р(A_m) log p(A_m) .

         Опыт a, состоящий в выяснении того, какой при этом сигнал будет принят на приемном конце, будет, очевидно, опытом с r исходами, зависимыми от опыта b. Условная вероятность исхода В_j этого нового опыта при условии, что опыт b имел исход А_i (i = 1, 2, 3, …, m; j = 1, 2, 3, …, r ) равняется р_Аi (В_j).

         Следовательно, информация об опыте b, содержащаяся в опыте a, будет иметь следующий вид:

I(a, b) = H (b) – H_a (b),

где Н_a (b) – условная энтропия опыта b при условии опыта a.

         Очевидно, что:

-     информация I(a, b) всегда не больше энтропии Н (b) опыта b, то есть информации, содержащейся в передаваемом сообщении;

-     информация I(a, b) равна энтропии Н (b) только в том случае, когда исход опыта a однозначно определяет исход опыта b, то есть когда по принятому сигналу можно всегда однозначно выяснить какой сигнал был передан (помехи отсутствуют);

-     информация I(a, b) равна нулю в том случае, когда опыт a не зависит от опыта b (очень сильные помехи, никакой передачи нет).

 

 

Вопрос 19. Влияние помех на линии связи. Пропускная способность линии с помехами

 

6.7. Влияние помех на линии связи. Пропускная способность линии с помехами

 

         При отсутствии помех пропускная способность C определяется как наибольшее число единиц информации, которое можно передать по этой линии связи за единицу времени. Обобщим это определение на случай линии связи с помехами. Для такой линии количество информации, получаемое на приемном конце при приеме одного элементарного сигнала,

I(a, b) = H (b) – H_a (b)  – величина, зависящая от вероятности р_А1(А₁), р_А2(А₂), р_А3(А₃), …, р_Аm(А_m) того, что передал сигнал А₁, А₂, …, А_m.

         Обозначим за  – наибольшее значение информации I (a, b), которое может быть получено при помощи изменения вероятностей р(А₁), р(А₂), р(А₃), …, р(А_m), и пусть это значение достигается при значениях р⁰(А₁), р⁰(А₂), р⁰(А₃), …, р⁰(А_m). При такой передаче количество информации, переданной за единицу времени,

 .

         Величина С называется пропускной способностью линии связи с помехами.

         Так как наибольшее значение I (a, b) не может превосходить Н (b), а  Н(b) £ log m, то очевидно, что пропускная способность линии связи с помехами всегда меньше, чем линии без помех. При r = m сигналы В₁, В₂, В₃, …, В_r совпадают с А₁, А₂, …, А_m и р_Аi(B_j) = 1, при j = i, следовательно, р_Аi(B_j) = 0 при i ¹ j, то есть всегда принимается тот же сигнал, что и был передан (помехи не препятствуют или же отсутствуют):

Н_a (b) = 0  и  с = max I (a, b) = max H (b) = log m.

         При этом С = L log m – уже известный случай.

 

 

Вопрос 20. Анализ двоичной симметричной линии

 

6.8. Анализ двоичной симметричной линии

 

         Пусть по линии связи передается два элементарных сигнала (А₁ – импульс, А₂ – пауза). Вероятность безошибочного приема любого из передаваемых сигналов примем за 1–р, а вероятность ошибки будет равна р. В этом случае

 

р_А1(А₁) = р_А2(А₂) = 1–р, а  р_А1(А₂) = р_А2(А₁) = р.

 

         Графически схему двоичной симметричной линии принято изображать согласно схеме (рис.13). На рис.13, а   отражена конфигурация передаваемого сигнала, а на рис.13,б показано, в какие принимаемые сигналы могут перейти передаваемые сигналы А₁ и А₂ и с какой вероятностью

 

                                                                                    

                    

 

          

                   а)                                    б)

Рис. 13. Схема двоичной симметричной линии: а - характер

сигналов А₁ и А₂;   б - схема преобразования сигналов

 

Для вычисления величины с воспользуемся равенством

 

I(a, b) = H (b) – H_a (b) .

Из схемы (рис.13,б) видно, что если передается сигнал А₁, то на приемном конце с вероятностью 1–р получим тот же сигнал А₁, а с вероятностью р – сигнал А₂. Аналогично с передачей сигнала А₂. Потому

                Н_А1(b) = Н_А2(b) = – (1–p) log (1–p) – p log p;

     H_a (b) = p(A₁) H_A1(b) + p(A₂) H_A2(b) = – (1–p) log (1–p) – p log p,

так как р(А₁) + р(А₂) = 1.

Отсюда легко сделать вывод о том, что в рассматриваемом случае

H_a (b) не зависит от вероятностей р(А₁) и р(А₂), и для вычисления с = max I(a, b) = max[H (b) – H_a (b)] надо определить только максимальное значение H (b). Величина H (b) – энтропии опыта b, имеющего только два исхода (рис.13, а) и поэтому  она не превосходит одного бита. Значение

H(b) = 1 достигается при р(А₁) = р(А₂) = 0,5, так как в этом случае оба исхода b будут равновероятными. В рассматриваемом случае  р⁰(А₁) =

= р⁰(А₂) = 0,5,

с = 1 +  (1–p) log (1–p) + p log p.

Следовательно, искомая пропускная способность двоичной симметричной линии будет равна

С = L[1 +  (1–p) log (1–p) + p log p].

Последняя формула показывает, как пропускная способность двоичной симметричной линии зависит от вероятности ошибки р.

 

 

 

 

 

 

 

 

 

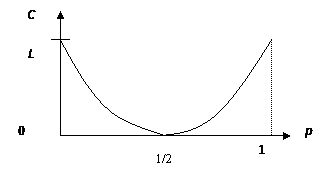Рис. 14. Зависимость пропускной способности двоичной симметричной линии от вероятности ошибки

 

Наибольшее значение C = L функция достигает при р = 0 (помехи отсутствуют) и р = 1 (А₁ ® А₂, А₂ ® А₁) помеха не мешает понять какой сигнал был передан. При р = 0,5 пропускная способность линии равна нулю. Независимо от того, какой сигнал был передан, мы получим на приемном конце с вероятностью 0,5 сигнал А₁ и с вероятностью 0,5 сигнал А₂. Принятый сигнал не будет содержать никакой информации.