Вопрос 11. Информация и алфавит

 

3.5. Информация и алфавит

 

Большая часть используемой информации сообщается  посредствам языка. В устной речи элементарным символом являются звуки, а в письменной речи слова составлены из букв. Знаки и буквы, организованные в определенные последовательности, несут информацию не потому, что они повторяют объекты реального мира, а по общественной договоренности об однозначной связи знаков и объектов (например, предметы и слова для их обозначения).

Информация, основанная на однозначной связи знаков с объектом реального мира, называется смысловой или  семантической.

Информация, заключенная в характере (порядке и взаимосвязи) следования знаков в сообщении, называется синтактической.

Наибольший интерес представляет получение семантической информации. Однако эффективная количественная мера семантической информации на сегодня не найдена. Существуют только косвенные методы оценки. Синтактическая информация поддается  измерению в строго определенном смысле. Полагают, что практическая ценность синтактической информации заключается в том, что семантическая информация (в конечном счете интересующая получателя) также заключена в последовательности знаков. Чем больше знаков используется, тем больше передается смысловой информации.

Рассмотрим особенности использования алфавита для хранения и передачи информации. Русский алфавит содержит 32 буквы. Однако в анализируемом алфавите имеется «нулевая буква» – пробел.

Если принять условия равновероятного появления букв в сообщении, то можно легко оценить неопределенность, приходящуюся на одну букву алфавита H₀ = log k = log 32 = 5 бит.

На самом деле появление букв совсем не равновероятно. Ориентировочные значения частот появления букв приведены в таблице

 

 

 

Приравняв эти частоты к вероятностям появления соответствующих букв, энтропия одной буквы

H₁ = H(a₁) = –0,175 log0,175 – 0,09l og0,09 – … -

 

–0,002 log0,002 = 4,35 бит  .

 

Из сравнения H₁ с величиной H₀ = 5 бит видно, что неравномерность появления различных букв в алфавите приводит к уменьшению информации, содержащейся в одной букве на 0,65 бит. Это обстоятельство позволяет уменьшить трудоемкость при передаче данных.

 

Вопрос 12. Избыточность в языке

 

3.6.  Избыточность в языке

 

При определении H₁=H(a₁) – энтропии опыта по оценке неопределенности, содержащейся в одной букве алфавита, мы считали, что буква независима. Это означает, что при составлении сообщения, в котором каждая буква содержит 4,35 бит информации, можно прибегнуть к помощи урны, в которой лежат тщательно перемешанные 1000 бумажек, из которых  175 не содержат ничего («пробел»), на 90 написана буква «О», на 72 – «Е» и т.д. Извлекая из такой урны бумажки, мы получим ничего не значащую фразу. Эта фраза будет похожа на русскую речь, но будет очень далека от разумного текста. Несходство полученной фразы с осмысленным сообщением объясняется тем, что на самом деле буквы в тексте не независимы друг от друга. Так, например, если мы знаем, что очередной буквой явилась гласная, то значительно возрастает вероятность появления на следующем месте согласной буквы и т.д.

Наличие в русском тексте определенных закономерностей приводит к дальнейшему уменьшению степени неопределенности одной буквы сообщения. Количественно это уменьшение можно оценить использованием условной энтропии H₂ = H_a1(a₂), которая является

энтропией опыта a₂, состоящего в определении одной буквы текста при условии, что нам известен исход опыта a₁, состоящего в определении предшествующей буквы.

Таким образом, особенности языка вносят определенную зависимость опытов, отражающихся в энтропии.

Известно, что с возрастанием числа букв в словах сообщения энтропия одной буквы уменьшается.  К.Шенноном введено понятие избыточности языка:

 ,

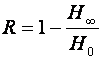Где 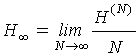   –  предельное значение энтропии с учетом вероятности сочетаний букв в словах сообщения,

 H₀ – средняя неопределенность букв (в русском алфавите H₀ = 4,35 бит).

 

Применительно к русскому языку избыточность заметно превышает 50 %. Это обстоятельство объясняется тем, что выбор следующей буквы осмысленного текста более, чем на 50 % определяется самой структурой языка и, следовательно, случаен лишь в сравнительно небольшой степени. Именно избыточность языка позволяет сокращать телеграфный текст за счет отбрасывания некоторых легко отгадываемых слов, предлогов, союзов. Она же позволяет легко восстанавливать истинный текст даже при наличии значительного числа ошибок в телеграмме или описок в книге.

 

Вопрос 13. Проблемы кодирования

 

6. Методы ОБРАБОТКИ и передачи 

    информации

 

6.1. Проблемы кодирования

 

         Рассмотрим общую схему передачи сообщений в информационных цепях или по линиям связи (рис.11).

 

 

                                       

 

                                                

        

Рис. 11. Передача информации в информационных цепях

 

         Проблема передачи информации является наиболее разработанной прикладной проблемой теории информации. Предположим, что на одной стороне линии связи отправитель желает передать сообщение, записанное при помощи 33 букв русского алфавита или 27 букв латинского алфавита, и 10 цифр. Применительно к телемеханике сигналами являются импульсы напряжения или тока. При помощи сигналов (импульс, пауза) можно передавать любые сообщения.

         Правило, сопоставляющее каждому передаваемому сообщению необходимую комбинацию сигналов называется кодом.

         Простейшими кодами являются коды Морзе и Бодо. В коде Морзе каждой цифре или букве сообщения сопоставляется последовательность коротких посылок – точек, и в три раза более длинных посылок – тире. Пробел отличается различительным знаком – длинной паузой. Код Бодо сопоставляет каждой букве некоторую последовательность из пяти простейших сигналов – импульсов и пауз одинаковой длительности.

         Допустим имеется сообщение, записанное при помощи некоторого алфавита, содержащего n букв. Требуется закодировать сообщение, то есть указать правило, сопоставляющее каждому такому сообщению, определенную последовательность из m различных элементарных сигналов, составляющих алфавит передачи. Естественно, что кодирование должно быть эффективным и экономичным. Считается, что кодирование будет тем эффективнее и выгоднее, чем меньше элементарных сигналов требуется затратить на передачу сообщения. Если каждый элементарный сигнал имеет определенную длительность, то наиболее выгодный код позволяет затратить на передачу сообщения меньше всего времени.

         Существует доказательство теоремы о том, что среднее число элементарных сигналов, приходящихся на одну букву сообщения не может быть меньшим числа log₂n (в случае двоичных сигналов). Любопытно, что если принять за n (число букв в алфавите) число реализаций статистического опыта, то log₂n будет соответствовать мера его неопределенности. В общем случае, когда используются не два, а m элементарных сигналов на кодирование каждой буквы, число элементарных сигналов будет равно:

 .

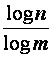         Значение понятия экономичности кода особенно возрастает при анализе сообщений статистическими методами. Не практике обычно приходится иметь дело с сообщениями, в которых частота появления отдельных букв значительно отличается друг от друга. Как мы уже отмечали ранее, например, частота появления букв "О" и "Щ" оценивается вероятностями 0,09 и 0,003. Поэтому основное значение играет теоретико–вероятностное среднее значение числа элементарных сигналов, приходящихся на одну букву передаваемого сообщения.

         В простейшем случае при использовании двоичных кодов, сообщению из n букв с вероятностями их появления р₁, р₂, …, р_n, где р₁ + р₂ + … + р_n = 1, может быть сопоставлен некоторый метод отгадывания заданного числа x, не превосходящего n, при помощи вопросов, на которые можно ответить только "да" или "нет". При заданных вероятностях р₁, р₂, …, р_n среднее число двоичных элементарных сигналов, приходящихся в закодированном сообщении на   одну   букву   исходного   сообщения,   не  может   быть   меньше   H,    где   H = – p₁ log p₁ – p₂ log p₂ – ……–

– p_n log p_n – энтропия опыта, состоящего в распознании одной буквы текста. Отсюда следует, что для записи сообщения из M букв требуется не меньше, чем МН двоичных сигналов.

         Если вероятности р₁, р₂, …, р_n не равны между собой, то

H < log n,

поэтому появляется возможность построения экономичных кодов за счет учета статистических закономерностей.

 

Вопрос 14. Код Шеннона-Фано

 

6.2. Код Шеннона-Фано

         Идея использования неравенства H < log n для построения экономичного кода очень эффективно используется в кодах, которые впервые предложили в 1948 – 1949 гг.  Р. Фано и К. Шеннон.

         Предположим, что алфавит содержит n букв. Расположим буквы алфавита в один столбик в порядке убывания вероятностей. Затем разобьем их на две группы – верхнюю и нижнюю. Для букв первой группы в качестве первой цифры кодового обозначения используем 1, а для букв второй группы – цифру 0. Далее, каждую из двух полученных групп снова разделим на две части с возможно более близкой суммарной вероятностью. В качестве второй цифры кодового обозначения используются цифры 1 и 0 в зависимости от того, принадлежит ли буква к первой или второй из этих подгрупп. Затем каждая из содержащих более одной буквы групп снова делится на две части и т.д. Процесс повторяется до тех пор, пока каждая из разделенных групп будет содержать по одной букве.

         Рассмотрим несложный принцип кодирования по методу Шеннона–Фано. Допустим, что алфавит содержит всего шесть букв, вероятности которых в порядке убывания равны 0,4; 0,2; 0,2; 0,1; 0,05; 0,05 (см. таблицу).

                  

         Основной принцип, положенный в основу кодирования по методу Шеннона-Фано заключается в том, что при выборе каждой цифры кодового обозначения стараются, чтобы содержащаяся в ней информация была наибольшей. Разумеется, количество цифр в различных обозначениях будет неодинаковым, то есть код Шеннона-Фано является неравномерным. Буквы, имеющие большую вероятность, получают более короткие обозначения, чем соответствующие маловероятные буквы. В результате, хотя некоторые кодовые обозначения здесь и могут иметь весьма значительную длину, среднее значение длины такого обозначения значительно уменьшается.

 

Вопрос 15. Анализ экономичности кода

 

6.3. Анализ экономичности кода

 

         В нашем примере шестибуквенного алфавита равномерный код состоит из трехзначных кодовых обозначений ( так как 2² < 6 < 2³ ). На каждую букву в лучшем случае приходится три сигнала. При использовании кода Шеннона-Фано среднее значение числа элементарных сигналов, приходящихся на одну букву сообщения, будет равно (данные берем из таблицы кодирования по методу Шеннона-Фано на с.45):

1´0,4 + 2´0,2 + 3´0,2 + 4´0,1 + 5´ (0,05 + 0,05) = 2,3 .

         Это значительно меньше, чем 3, и не очень далеко от значения энтропии Н:

 

Н = –0,4´ log 0,4 – 2´0,2´ log 0,2 – 0,1´log 0,1 – 2´0,05´log 0,05 = 2,22.

         Если провести аналогичный анализ для алфавита, состоящего из 18 букв, то равномерный код будет иметь пятизначное кодовое обозначение, а код Шеннона-Фано будет иметь буквы даже с семью двоичными сигналами, но зато среднее число элементарных сигналов, приходящихся на одну букву, будет равно 3,29 и это немного отличается от величины энтропии Н = 3,25. Особенно выгодно кодировать по методу Шеннона-Фано не отдельные буквы, а сразу целые блоки из нескольких букв. Даже в неблагоприятных случаях кодирование целыми блоками позволяет приближаться к величине энтропии. Рассмотрим пример, когда имеются лишь две буквы А и Б с вероятностями р(А) = 0,7 и р(Б) = 0,3.

 

Тогда                Н = –0,7 log0,7 – 0,3 log0,3 = 0,881 .

 

         Применение метода Шеннона-Фано к исходному двухбуквенному алфавиту здесь оказывается бесцельным. Он приводит нас к простейшему равномерному коду, требующему для передачи одного двоичного знака.

 

        

Здесь мы имеем превышение Н на 12 %. Если применить код Шеннона-Фано к кодированию всевозможных буквенных сочетаний, то

 

 

среднее значение длины кодового обозначения в этом случае

1´0,49 + 2´0,21 + 3´0,21 + 3´0,09 = 1,81 .

         На одну букву приходится 1,81 / 2 = 0,905, что лишь на 3% больше

Н = 0,881 бит. При использовании трехбуквенных комбинаций средняя длина кодового обозначения 2,686, то есть на одну букву приходится 0,895 двоичных знаков, что всего на 1,5% больше Н.

         Рассмотренные примеры анализа степени близости среднего числа двоичных знаков, приходящихся на одну букву сообщения, к значению Н может быть увеличено при помощи перехода к кодированию еще более длинных блоков. Этому обстоятельству посвящена основная теорема кодирования.

         При кодировании сообщения, разбитого на N–буквенные блоки, можно, выбрав N достаточно большим, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близким к Н.