Вопрос 1. Неопределенность

1. Неопределенность

Фундаментальным понятием в теории информации является неопределенность. Изучением этой проблемы занимались еще античные философы, которые полагали, что неопределенность – это отсутствие каких-либо количественных характеристик материи, заполняющей пространство. Гегель считал, что неопределенность является первичной в переходе неопределенности в определенность.

Можно сформулировать некоторые свойства неопределенности:

- неопределенность присутствует в пространстве, во времени и материи;

- везде, где присутствует неопределенность, создаются предпосылки для получения информации;

- неопределенность обладает жизненным циклом (выявление, уменьшение, увеличение неопределенности) при получении информации она переходит в определенность;

- неопределенность измеряется от 0 до бесконечности: 0 – ситуация полной определенности; ¥ – ситуация полной неопределенности.

Представляя неопределенность, как источник информации, мы должны ясно представлять, в каком пространстве и каких границах она действует.

Весь окружающий нас мир состоит из систем, начиная от ядра атома и кончая вселенной. Следовательно, можно говорить о неисчерпаемости неопределенности и ее производной-информации. Известно, что объем информации растет, по крайней мере, вдвое быстрее промышленного потенциала общества. По подсчетам науковедов увеличение информации в обществе в начале нашей эры происходило в следующем темпе: первое удвоение знаний – 1750 г., второе – 1900 г., третье – 1950 г., четвертое – 1970 г., пятое –1980 г.

Предполагается, что к концу второго тысячелетия темпы накопления знаний и, следовательно, информации еще более возрастут.

1.1. Неопределенность в элементах систем. Факторы при исследовании объектов

Под системой понимается упорядоченная совокупность взаимодействующих элементов или частей. Поскольку понятие «система» имеет очень широкий смысл, любой исследуемый объект может быть рассмотрен как система (рис. 1).

К основным свойствам системы относятся:

- целостность (зависимость элементов системы от их места);

- структурность (возможность описания системы посредством структуры и связей;

- взаимозависимость системы и среды (например, внешней среды);

- иерархичность (система может делиться на подсистемы).

Рис. 1. Представление объекта как элемента системы:

{х}, {У}- входные и выходные множества параметров;

{ƒ} – возмущающие воздействия.

Понятие система может охватывать как материальные объекты, так и информационные процессы. Неопределенность в системе – это ситуации, когда полностью или частично отсутствует информация о возможных состояниях системы и внешней среды, иначе говоря, когда в системе происходят те или иные непредсказуемые события. Это неизбежный спутник больших (сложных) систем. Чем сложнее система, тем большее значение приобретают факторы неопределенности.

Источниками и причинами возникновения факторов неопределенности являются сами системы, мотивация поведения лиц, принимающих решения. Применительно к системам управления к факторам неопределенности относят:

- факторы слабой структуризации системы;

- стохастичности окружающей среды;

- факторы риска;

- недостаточности информации;

- факторы нестабильности и т.д.

Вопрос 2. Возникновение и развитие теории информации

1.2. Возникновение и развитие теории информации

Фундаментальные понятия теории информации заложены в работах К. Шеннона, Н. Виннера, А. Колмагорова, Д. Фон-Неймона. Предпосылками к появлению теории информации явились изменения роли человека в производственных отношениях и прежде всего изменение структуры

технологической машины. На ранних этапах развития общества практиковалась трехзвенная структура (рис. 2, а).

Человек занимался непосредственно управлением такой машиной.

В более позднее время появилась четырехзвенная структура (рис. 2, б)): контрольно-управляющее устройство – двигатель – передающий механизм – исполнительный механизм.

а)

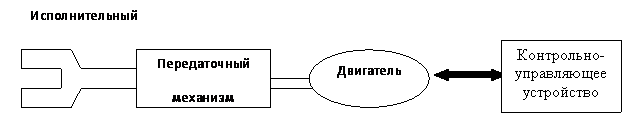
б)

Рис. 2. Структура технологической машины: а) трехзвенная;

б) четырехзвенная

Роль человека сведена к слежению и наладке машины. Произошла автоматизация производства. Необходимость создания средств контроля и управления предопределило разработку теоретических методов представления, обработки и передачи информации.

Помимо производства, с появлением вычислительной техники и средств связи происходит частичная автоматизация умственного труда.

В настоящее время главенствующей стратегией развития общества является его информатизация (рис.3).

Информационные системы, сети и технологии используются не только в производственных отношениях, но и в быту современного человека.

Оформление теории информации как самостоятельной науки следует отнести к 1948-1949 гг., когда появились работы К. Шеннона. Статистические рассуждения К. Шеннона были восприняты как неожиданность, хотя по своей сути они являлись развитием идеи статистической термодинамики, основы которой были заложены Л. Больцманом. Не случайно общность математического аппарата этих теорий доходит до совпадений основных формул.

Дальнейшее развитие теории информации связано с именами Р. Хемминга, Л. Брюллюэна, А. Харкевича.В теории был развит достаточно мощный математический аппарат. Был решен ряд прикладных проблем в теории связи, кодирования и в других инженерных направлениях.

В настоящее время теория информации является активно развивающейся наукой. Оправдывается предсказание Н. Виннера: «Если ХVII столетие –

век часов, а ХVIII и ХIХ века - паровых машин, то ХХ – век связи и

управления. Связь, без которой не может быть управления, означает

Подпись: Объемы
информации

Комплексная

Рис. 3. Автоматизация и информатизация производственных отношений.

передачу информации. Если в ХVII веке были получены выдающиеся результаты в механике, а ХVIII и ХIХ веках - в термодинамике, то ХХ век ознаменовался развитием теории информации.

Вопрос 3. Логарифмическая мера неопределенности

2. ЭНТРОПия как мера неопределенности

2.1. Логарифмическая мера неопределенности

Поскольку понятие неопределенность носит в теории информации базовый характер, постараемся придать этому понятию количественную меру. Наиболее конструктивным подходом по оценке неопределенности является статистический подход. Он основывается на анализе неопределенности, как условия некоторого статистического опыта, имеющего случайную природу. Главным свойством случайных событий является отсутствие полной уверенности в их неотступлении. Очевидно, что степень этой неопределенности может быть различной. Рассмотрим ситуацию, в которой может произойти k различных событий или исходов, но при условии, что они считаются равновероятными. Естественно, чем больше неопределенность исходной задачи, тем больше k. Поэтому разумно степень неопределенности ситуации связывать с величиной k:

- если k =1, то исход опыта неслучайный;

- если k >1, то появляется неопределенность.

Таким образом, искомая количественная характеристика степени неопределенности зависит от k, т.е. является функцией ƒ(k). При k=1, эта функция должна обращаться в нуль (ибо неопределенность отсутствует), а при возрастании k функция ƒ(k) должна возрастать. Рассмотрим дополнительные требования к ƒ(k) вытекающие из статистических рассуждений для двух независимых опытов β и α (независимыми можно считать такие опыты, исходы которых не влияют на вероятность исходов друг друга). Предположим:

опыт α имеет m равновероятных исходов;

опыт β имеет l равновероятных исходов.

Сложный опыт αβ, состоящий в одновременном выполнении опытов α и β, должен иметь ml равновероятных исходов. Это очевидно, т.к. в сложном опыте αβ к неопределенности опыта α добавляется неопределенность опыта β. Поэтому естественно предположить, что степень неопределенности опыта αβ равна сумме неопределенностей, характеризующих опыты α и β.

Следовательно, условие, которому должна удовлетворять функция ƒ(k), может быть выражено свойством аддитивности:

ƒ(ml) = ƒ(m)+ ƒ(l) .

Очевидно, что всем вышеизложенным требованиям удовлетворяет логарифмическая функция, и за меру неопределенности опыта, имеющего k равновероятных исходов, разумно принять число log k. Такая мера согласуется с условиями:

log (ml) = log m + log l ;

при k=1 log k =0; при возрастании k log k возрастает.

Следует отметить, что выбор основания логарифма здесь несущественен, т.к.

и переход от одной системы логарифмов к другой сводится к умножению функции ƒ(k)= log k на постоянный множитель (модуль перехода log_ba).

В конкретных применениях единицы измерения степени неопределенности обычно используют двоичные логарифмы:

ƒ(к)= log₂k .

Однако для оценки неопределенности иногда используют и другие основания логарифма, например натуральные логарифмы ln k.

Использование двоичных логарифмов означает, что за меру неопределенности принимается неопределенность, содержащаяся в опыте, имеющем два равновероятных исхода. Такая единица измерения неопределенности называется «двоичной единицей» или битом. В немецкой литературе используется «Ja-Nein Einheit» «да-нет единица».

Например, в опыте с подбрасыванием монеты k=2, log₂2=1 бит, а в опыте с колодой из 32 различных карт при выборе одной из них неопределенность оценивают 5 двоичными единицами, т.к. 32=2⁵. Возьмем две колоды по 32 карты в каждой. Если мы выберем две карты по одной из каждой колоды, то очевидно неопределенность должна возрасти вдвое. Общее число исходов К=К₁К₂, где К₁=К₂=32=2⁵, и следовательно, К=2¹⁰.

Логарифмическая оценка неопределенности подтверждает данные утверждения:

log (k) = log (k₁k₂)= log k₁ + log k₂=10 бит.

Исчисление неопределенности в битах означает, что ответы на вопросы по уменьшению неопределенности даются в форме «да» или «нет».

Известна библейская история о Бар-Кохбе. В римский лагерь был послан лазутчик. Он был пойман и ему отрезали язык и отрубили руки. После этого он был отпущен и вернулся к своим. Естественно, что он не мог ни говорить ни писать. Однако военоначальник Бар-Кохба получил сведения о врагах, задавая вопросы, на которые несчастный отвечал кивком головы.

Вопрос 4. Энтропия. Формула Шеннона

2.2. Энтропия. Формула Шеннона

Рассмотрим статический опыт, имеющий k равновероятных исходов. Таблица вероятностей такого опыта имеет следующий вид.

Исходы опыта	А₁	А₂	А₃	…	А_k
Вероятности	1/k	1/k	1/k	…	1/k

Общая неопределенность этого опыта может быть оценена величиной

log k .

Каждый отдельный исход, имеющий вероятность 1/k, вносит неопределенность, равную

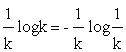В том случае, если исходы имеют различную вероятность, (см. таблицу вероятностей),

Исходы опыта	А₁	А₂	А₃
Вероятности	1/2	1/3	1/6

то исходы А₁, А₂, А₃ вносят соответственно неопределенность равную:

В случае независимости исходов общая неопределенность опыта будет равна:

Обобщая рассмотрение вышеизложенного, можно для опыта α с таблицей вероятностей

Исходы опыта	А₁	А₂	…	А_k
Вероятности	p (А₁)	p (А₂)	…	p (А_k)

сделать оценку в виде

В результате для опыта α мы получаем число, являющееся количественной мерой неопределенности опыта. Эта величина называется энтропией, а формула Шеннона для расчета энтропии имеет вид:

Вопрос 5. Ограничения в использовании оценок неопределенности

2.4. Ограничения в использовании оценок неопределенности

Проведем анализ мер оценки неопределенности и, следовательно, возможности получения информации. Величина logk, где k – количество исходов опыта, полностью игнорирует различие между характером имеющихся исходов. Маловероятному исходу здесь придается такое же значение, как и исходу весьма достоверному.

Шеннонская энтропия является усредненной мерой. Здесь исходу Аi опыта α. приписывается неопределенность равная –log p(A_i). Далее в качестве меры неопределенности всего опыта α. принимается среднее значение случайных величин

с вероятностями соответственно р(А₁); р(А₂); р(А₃); …; р(А_k), чем и является

Рассмотрим примеры применяемости предлагаемых мер неопределенности. Допустим, нам интересно знать, сдал или не сдал экзамен некий студент. Примем следующие условия этой задачи: вероятности p _(сдал)=7/8; p _{(не
сдал)} = 1/8;

Очевидно, что мы имеем дело с довольно сильным студентом. Если нам сообщили, что он сдал экзамен, мы вправе сказать: «Ваше сообщение мне мало что дало, я и без этого предполагал, что он сдаст экзамен». Если за оценку неопределенности принять

H(a) = -log p,

то .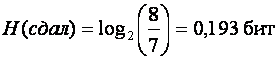

Если нам сообщили, что он не сдал, то мы получим большее количество информации:

H (не сдал) = + log₂8 =3 бит

Как было уже отмечено Шеннонская оценка является усредненной оценкой:

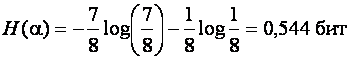В рассмотренном примере статистические неопределенности не содержат оценки ценности информации. Теорема Эйнштейна имела бы, вероятно, для математика гораздо большую ценность, чем заметка в газете. С другой стороны, для рядового читателя газетная новость может иметь ценность, тогда как теорема почти наверняка не будет иметь для него ценности.

Выберем более тривиальный пример. Неопределенность при выборе одной из 32 карт составляет 5 бит. Она всегда измеряется этим числом 5 бит, хотя выбранная карта может быть тузом и семеркой или королем. Ценность этих карт зависит от правил игры.

Приведенные примеры явно показывают пределы применяемости статистических оценок, и эти пределы нужно иметь в виду при использовании теории информации.