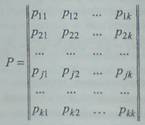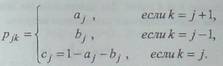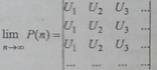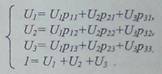. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Информационным
процессом называют процесс, возникающий в результате установления связи между
объектами интерактивного цикла: источником информации и её приемником или получателем.
Принято отмечать три
составляющие информационных процессов:
- Восприятие некоторого физического
явления или сигнала и преобразования его формы;
- изменение модели внешнего мира под воздействием принятого
сигнала;
- пространственно-временная
передача сигналов.
Понятие сигнала связано с
вещественно-энергетической опосредовательностью информационного процесса.
Сигнал - это материальный носитель информации, способный изменить модель внешнего
мира.
особым видом
сигнала являются
знаки, которые, в отличие от сигналов естественного происхождения, создаются
людьми и предназначаются для передачи и хранения информации.
На
рис.1 представлена функциональная схема информационного процесса:
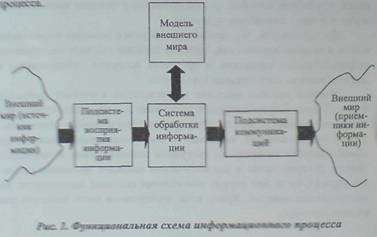
Внешний мир воздействует
на подсистему восприятия информации, выступая при этом как источник информации.
Интерпретирующая подсистема информационной системы представлена в виде системы
обработки информации и модели внешнего мира. Подсистема коммуникации осуществляет передачу обработанной информации во
внешний мир, выступающий в этом случае в
роли приемника информации.
Предметом изучаемой науки являются
информационные процессы, понимаемые в
широком смысле как процессы получения, хранения, транспортировки, преобразования информации, взятые по
отдельности или в совокупности.
Содержание и характер информационного процесса определяется
информационной системой, в которой он протекает.
Объектом деятельности инженера специалиста
по информационным процессам являются автоматизированные информационные системы,
т.е. человеко-машинные комплексы.
Следовательно, теория информационных процессов должна включать в свой состав
проблемы, связанные с преобразованием
информации технической системой, человеком, коллективом людей. Это определяет
особый характер методологий информационных процессов, объединенных понятием - системный
подход.
Для рассмотрения задач системного подхода
при исследовании информационных процессов введем основные определения и
понятия:
- Система есть совокупность
элементов, которые в свою очередь при
определенных условиях могут
рассматриваться как система, а сама иссле
дуемая система - как один из элементов более широкой системы.
- Интегративные свойства — это свойства, присущие системе в це
лом, но не свойственные ни одному из
элементов в отдельности. Отсюда
следует очень важный вывод: система
не сводится к простой совокупности
элементов, и, расчленяя систему на
отдельные части, изучая каждую из
них в отдельности, нельзя познать все свойства системы в целом.
- Связи между элементами
системы превосходят по силе и мощности
связи с
элементами, не входящими в систему. Указанное свойство позво
ляет
выделить систему в виде целостного объекта из окружающей среды.
- Модель - описание системы, отображающее определенную группу
ее свойств. Модель позволяет предсказывать
поведение системы в опреде
ленном диапазоне условий.
Описание системы
можно рассматривать с нескольких точек зрения:
а) функциональной;
б) морфологической;
в) информационной.
Функциональное
описание необходимо для того, чтобы осознать суть системы, определить ее место, оценить
отношение к другим системам и к внешней среде. Здесь необходимо ввести следующие
понятия: состояние -множество существенных свойств, которыми система обладает в данный момент времени;
внешняя среда - множество элементов, которые не входят в систему, но
изменение их состояния вызывает изменение состояния системы; модель
функционирования системы — модель, предсказывающая изменение состояния
системы во времени,
Морфологическое
описание даёт представление о строении системы. Оно не может быть исчерпывающим.
Глубина описания, уровень детализации, т.е. выбор элементов, внутрь которых
описание не проникает, определяется назначением системы и целью исследования.
Изучение морфологии начинается с элементного состава. Под элементом в данном случае
понимается подсистема, внутрь которой описание не проникает. В результате
морфологического описания возникает понятие структуры. Структура — совокупность
элементов и связей между ними.
Информационное
описание системы даёт представление об организации системы. Оно определяет
зависимость морфологических и функциональных свойств системы от количества
внутренней (о себе самой) и внешней (из среды) информации.
Методологическая
специфика подхода определяется тем, что он ориентирует исследование к раскрытию
целостности объекта и обеспечивающих ее механизмов, а также на выявление многообразных
типов связей сложного объекта и сведение их в единое теоретическое описание.
Информационные процессы можно
рассматривать как процессы, протекающие внутри такого класса систем, который
называется информационными системами (ИС).
Необходимость
системного подхода при создании ИС объясняется тем, что темпы развития науки и техники
с каждым днем увеличиваются, сложность систем возрастает, а это увеличивает
длительность разработки, в результате чего к моменту ввода их в эксплуатацию они
могут быть морально устаревшими, а иногда и просто не нужными. Проектирование ин-
8
формационных систем иногда требует больших
капиталовложений, в результате чего требуются гарантии того, что будет создана
система с нужными свойствами.
Необходимость создания
современных ИС привела к активному использованию системного подхода в технике, в
результате чего появилась новая научно-техническая дисциплина «Системотехника»,
охватывающая вопросы проектирования сложных систем.
К числу
задач,
решаемых на уровне системного подхода, обычно
носят:
- определение общей структуры
системы;
- организацию
взаимодействия между подсистемами;
- учет влияния внешней
среды;
- выбор структуры;
- построение алгоритмов
функционирования.
Проектирование сложных систем принято разбивать на две стадии.
макропроектирование и микропроектирование. На уровне макропроектирования решаются
функционально-структурные вопросы системы в целом. Микропроектирование
связано с разработкой элементов системы как физических единиц оборудования и с
получением технических решены основным элементам.
Рассмотрим основные
этапы макропроектирования.
1. В начале проектирования
необходимо правильно и четко опреде-
лить
главную цель разработки, которая преследуется при создание новой
системы. В
результате уяснения можно выявить главную цель (как напри-
мер,
увеличение пропускной способности информационно-справочной
системы, либо минимизацию времени контроля сложного объекта) или не-
сколько
разных целей, которые преследуются одновременно. Например, в
информационной системе
"Сирена" резервирование билетов на самолёты -
увеличение
пропускной способности и уменьшение стоимости системы.
2. Необходимо четко оговорить внешние
условия, в которых будет
функционировать
проектируемая система:
а) нужно выделить те
связи с внешней средой, которые являются наиболее существенными и
которые необходимо учитывать при проектировании;
б)
задать приближенное описание этих связей, для чего могут быть использованы как опыт эксплуатации
аналогичных систем, так и статиста-
ческие данные, полученные в результате специально
проведенных исследований.
3. Необходимо осуществить
оценку эффективности системы, которая характеризуется степенью соответствия системы к выполнению поставленных
перед нею задач. Для количественной оценки эффективности выбирают один или несколько показателей (критериев).
Например, автоматизирования система
контроля (АСК) сложного оборудования может иметь показатели, характеризующие
достоверность контроля. В этом случае при проектировании АСК основное внимание
будет уделяться вопросам обеспечения
максимальной достоверности, но в этом случае в меньшей степени будет
учитываться другое важное свойство системы - быстродействие.
Рассмотренный пример убеждает в том, что
выбор показателей эффективности необходимо проводить после глубокого анализа
целей и задач, поставленных перед системой.
После формулировки
проблемы обычно приступают к определению одного или нескольких вариантов построения
системы.
Зависимости между
параметрами ИС являются разнообразными и сложными, в результате чего построение
единой математической модели оказывается затруднительным. Поэтому для
моделирования таких ИС используют принцип многоуровневого (иерархического)
описания. Применение многоуровневой модели вытекает из необходимости упрощения
методов ее построения и
необходимости учета большого числа характеристик
ИС:
- уровень 1 -
информационное описание, соответствующее взгляду
на
систему в целом и на ее взаимодействие с внешней средой;
- уровень 2 - функциональное описание.
Уровень функционального
описания выявляет способ реализации алгоритмов системы и определяет
множество функциональных элементов ИС и
отношений между ними;
- уровень 3 -
системотехническое описание. Уровень этого описания
выявляет
структуру комплекса технических средств ИС, под которым по
нимается
состав и связи функциональных групп оборудования, номенкла-
тура, число и размещение технических средств каждой
функциональной группы.
Выбор уровня описания
зависит главным образом от цели исследования. Для многих систем выбор уровня
описания является естественным и определяется назначением системы. Выделение нескольких
уровней позволяет
вести параллельное построение моделей на каждом уровне различными
специалистами.
На каждом из уровней
имеется свой набор понятий и принципов, составляющих язык описаний, описаний
системы. Таким образом, в соответствии с иерархией уровней возникает иерархия
языков описания ИС.
Понимание системы
возрастает при последовательном переходе от одного уровня к другому: чем ниже
производится спуск по иерархической лестнице, тем более детальным становится
раскрытие систем; чем выше мы поднимаем уровень иерархии, тем яснее становится смысл
и назначение всей системы. Решение системотехнических задач для ИС возможно только на основе
многоуровневого принципа построения моделей.
2.
МОДЕЛИРОВАНИЕ
ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
И СИСТЕМ
Формализация общей схемы процесса
функционирования систем, включая ИС,
основана на следующих положениях:
- любая система
функционирует во времени, взаимодействуя со
внешней
средой, и в каждый момент времени может повторяться в одном
из
возможных состояний;
- на вход системы
поступают входные сигналы;
- система может выдавать
выходные сигналы;
- состояние системы в
данный момент времени определяется преды
дущими состояниями и входными
сигналами, поступившими в данный
момент времени и ранее; выходной сигнал в
данный момент времени оп
ределяется состояниями системы и
входными сигналами, относящимися к
данному и предшествующим состояниям.
Формализуем рассмотренные
положения.
11
1. Множество моментов времени t, в котором
рассматривается функционирование
системы, обозначим T. Множество Т в общем случае является подмножеством множества действительных
чисел и может быть непрерывным, дискретным или дискретно-непрерывным.
Дискретно-непрерывный характер относится к иерархическим системам.
Нижний уровень - непрерывная система (датчики, механические устройства), а верхний уровень - ЭВМ .
Функционирование системы во времени
рассматривается как процесс перехода
системы из состояния в состояние. Следовательно, прежде чем рассматривать
функционирование системы, необходимо определить множество состояний Z. Возможны различные
способы определения состояний.
1. Состояние системы определяется как совокупность состояний элементов системы. Если элементы системы могут
находиться в двух состояниях, то система, составленная из п элементов,
может находиться в одном из 2n состояний. Так
определяется состояние дискретных автоматов в вычислительной технике, сложных
систем при анализе надежности характеристик и т. д. Таким образом:

где
множество состояний Z дискретно.
2. Состояние системы
характеризуется некоторым целым неотрица
тельным числом z (z = 0, 1, 2,...). Так определяется состояние
при анализе
сложных
информационных систем с одной фазой обслуживания. В этом
случае z - число задач, запросов, находящихся в системе (на обслужива
нии либо в очереди).
3. Случаем, обобщающим
второй, является вариант, когда состояние
системы описывается набором целых неотрицательных чисел:
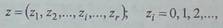

Подобный подход в
определении состоянии используется при описании динамики многофазных
многоэтапных систем типа телеавтоматических систем массового обслуживания.
4 Состояние системы определяется набором действительных чисел. Например, положение самолета можно в данный
момент времени описать вектором
фазовых координат (z1,z2,z3), z1, - наклонная
дальность, z2 -
азимут, Z3 - угол.
В обшем случае,
охватывающем все рассматриваемые варианты, будем считать, что состояние, рассматриваемой ИС, Z описывается некоторым набором
характеристик zi,zi E Zi, (i = 1,2,...,k), где Zi -заданные множества, а множества возможных состояний
ИС определяется как прямое произведение множеств
Z1,:

2. На вход любой сложной системы могут
поступать входные сигна
лы х е Х0,
где Х0 - множество входных сигналов. Входной сигнал,
поступающий
в систему в момент t еТ, обозначим x(t). В общем случае
будем
предполагать, что входной сигнал описывается набором характери
стик x1 е Х1 (i=1,2,...,m), где Xi заданные
дискретные или
непрерывные
множества.
Прямое произведение
вида
X = Х1 * Хг
* Х3. * ... * Хi. *...* Хт
будем называть пространством входных
сигналов, а входной сигнал х представляет
собой точку пространства X, описываемую координатами
x1,x2,...,xi,...,xm.
Отображение х = L(t), сопоставляющее каждому
моменту t e Т некоторый сигнал х
€ Х0,, называется входным процессом L(t).
3. Система способна
выдавать выходные сигналы у e Y0, где Y0 -
множество
выходных сигналов. Выходной сигнал, выдаваемый системой в
момент t e T, обозначим за y(t). Если выходной сигнал у
описывается
набором
характеристик у1, уг,..., уг,...,уп,
таких, что у1 e Yi, (i = 1,2,..., n), а
Yi — заданные множества, то прямое произведение
Y = Y1хY2х...хYi.х...хYn
называется
пространством выходных сигналов. По аналогии с входным процессом
определяется понятие выходного процесса:
у = М(t).
Принято информационные
системы относить к классу систем без последействия. Система без последействия
- система, будущее поведение которой определяется ее настоящим состоянием и
оно не зависит от прошлого; иначе говоря, состояние z(f) системы без
последействия в момент времени t > t0 определяется
состоянием z(t0) и участком процесса х
=L(t) за
интервал (t0,t), но не
зависит от предыстории поведения системы, от того,
каким образом система пришла в состояние z(t0). Различают два класса ИС без
последействия: детерминистические системы без последействия; стохастические
системы без последействия.
Динамика для
детерминистических систем будет считаться заданной, если указаны операторы
переходов Н и выходов G.
1. Оператор переходов Н определяет динамику переходов системы из состояния в состояние:
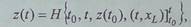
где z(t) - начальное
состояние, z(t0)eZ; t0 еТ, teT;
- множество
всевозможных участков входного процесса х = L(t), соответствующих интервалу
[t0, t]. При фиксированных t0,z(f0) и [t, xl]'t0 оператор Н реализует
отображение z = H(t) или z = z(t) множества Т во
множество Z, которое называется движением системы. Множество
всевозможных движений системы можно обозначить
{z(t)}.
Совокупность упорядоченных пар (t,z) для всех моментов teT, где z определяется заданным
движением z = z(t), называется фазовой траекторией
системы. Совокупность точек пространства Z, соотвегствующих в силу отображения z = z(t) всем моментам t e Т, называется траекторией
системы в
пространстве состояний.
2. Оператор выхода
системы G определяет динамику выходных сигналов:
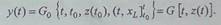
Для задания обобщенной
динамики ИС операторы H и G объединяют в виде оператора F = H х G, обозначая его как
оператор функционирования
системы.
2.2. МОДЕЛИ МАРКОВСКИХ
ПРОЦЕССОВ
Каждый раз, сталкиваясь
с явлением или процессами случайного характера, будем предполагать существование некоторого «экспериментатора», наблюдающего за исходом эксперимента. При
этом строго соблюдается некоторый
комплекс условий. Исход опыта - случайное событие, т.е. такое, которое в
ходе эксперимента может произойти, а может не произойти.
Мерой «случайности»
события является вероятность - числовая характеристика случайного события,
принимающая значения от 0 до 1:
-
случайные
события с нулевой вероятностью называются не
возможными
событиями;
-
события,
вероятность которых равна 1, называются достовер
ными
событиями, они всегда появляются в результате эксперимента;
-
события,
вероятность которых больше 0, но меньше 1, могут
появляться
при наблюдении, но могут и не появляться.
Вероятность
случайного события можно оценить приближенно как отношение числа опытов, в
которых событие произошло, к общему числу опытов. При этом достоверность проведенной
оценки тем выше, чем больше проведено опытов.
Существует класс
случайных событий, имеющих числовые значения. Принято говорить, что в подобных
опытах наблюдается не случайное событие, а случайная величина (опыт с
игральной костью).
Здесь роль случайных
событий играют возможные значения случайных величин. В зависимости от того,
какова мощность множества возможных значений случайной величины, различают
дискретные и непрерывные случайные величины.
Для полной
характеристики дискретной случайной величины достаточно перечислить ее
возможные значения и указать их вероятности. Например, таблица, «генерируемая»
игральной костью:
|
Xi
|
1
|
2
|
3
|
4
|
5
|
6
|
|
p(xi)
|
1/6
|
1/6
|
1/6
|
1/6
|
1/6
|
1/6
|
Здесь Xi - возможное
значение случайной величины, р(хi ) - вероят-ность появления
данного значения.
Случайные величины, в
отличие от их возможных значений обозначаются большими латинскими буквами: X, Y,,....
Для описания
непрерывной случайной величины обычно используются:
а) функция
распределения, определяемая как вероятность того, что случайная величина X меньше некоторого,
наперед заданного ее значения, выступающего в качестве аргумента функции F(x)=P(X<x);
б) плотность вероятности, определяемая как
предел отношения вероятности попадания
случайной величины X в интервале /\x, примыкающей
непосредственно в точке x к этому интервалу при стремлении /\х к
нулю:

Между функцией разделения и плотностью вероятности имеется следующая связь:
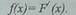
Кроме
этого существуют и другие формы описания случайных величин, например законы
распределения.

Под
случайным процессом понимается функция времени Xt (рис.2), значениями которой являются
случайные величины. Таким образом, случайный процесс можно рассматривать как
семейство случайных величин {Xt}, где t — временной параметр.
Функция, полученная в
результате наблюдения над случайным процессом, называется выборочной функцией
или реализацией случайного процесса. Выборочная функция ставит в соответствие
каждому значению временного
параметра t e T одно из возможных значений случайной вели-чины Хt . Область возможных
значений функции Xt называют пространством состояния L случайного процесса.
Конкретные значения хt случайного процесса Xt, наблюдаемые в ходе эксперимента в моменты
времени t, являются неслучайными величинами, поэтому любую
реализацию случайного процесса, полученную в результате наблюдения,
следует рассматривать как детерминированную функцию
времени.
С помощью одной
реализации нельзя дать полную характеристику случайного процесса. Каждая новая
реализация, полученная в результате наблюдения, дополняет сведения о свойствах
этого процесса. Поэтому понятие о случайных процессах обычно связывают с некоторым
ансамблем функций
- множеством функций, заданных явно или с помощью какого-либо признака.
Наиболее распространена классификация
случайных процессов по свойствам пространства состояний L, временного параметра Т
и статистическими зависимостями между случайными величинами {Xt}.
По
признакам L можно выделить два класса случайных
процессов:
- если множество
возможных случайных величин {Xt} конечно и
счетно,
то процесс относят к классу дискретных случайных процессов;
— процессы, для которых пространство
состояний эквивалентно множеству действительных чисел, относят к процессам с
непрерывным пространством состояний.
По
признакам T различают процессы:
а) с
непрерывным временем;
б) с
дискретным временем.
В первом случае переходы из одного
состояния в другое могут осуществляться: в любые моменты времени, а во втором случае
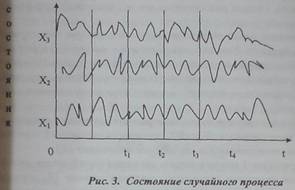
- в строго определенные моменты времени t0, t1, t2... (рис. 3).
Таким образом, с
учетом приведенных факторов, можно различить 4 типа случайных процессов:
- дискретный случайный
процесс с дискретным временем. Он явля
ется
пересечением класса процессов с дискретным пространством состоя
ний и
класса процессов с дискретным временем. Иногда такие процессы
называются
дискретными случайными цепями;
- случайный процесс с
дискретным временем отличается от первого
типа тем,
что имеет непрерывное пространство состояний;
- дискретный случайный процесс с непрерывным
временем имеет
дискретное пространство состояний и
относится к процессам с непрерыв
ным временем;
|
- случайный процесс
общего типа - процесс с непрерывным про-странством состояний и непрерывным временем.
|
В основном состояние
информационных систем характеризуется случайным характером протекающих в них процессов, проходящих под воздействием окружающей среды и входящих воздействий.
Разновидно-стью случайных процессов являются марковские процессы.
Пространство состояний дискретного
марковского процесса представляет собой конеч-
ое
или счетное множество, которое может быть отождествлено с множе-ством неотрицательных чисел (0, 1, 2,...}. Дискретный
марковский процесс с дискретным временем,
называемый цепью Маркова, характеризуется тем, что переход от одного состояния к другому возможен лишь в дис-
кретные моменты
времени t0, t1, t2............... При этом абсолютные
значения мо-
ментов
времени роли не играют. Поэтому обычно временной параметр Т отождествляют со множеством индексов {О, I, 2...} и тогда цепь Маркова
имеет вид
Х0, X1, X2,... Ври определенной зависимости
случайных величин Xt (i=0, I, 2,...).
Здесь X1 - случайная величина, принимающая
значения из множества L = {1, 2, 3, ...), в i = 0, I, 2, 3, ... - моменты времени.
Частным случаем цепи
Маркова может служить последовательность Xо,X1;.X2,.... полученная
путем независимых испытаний с исходами 1. 2 ..... Каждому исходу j сопоставлена
вероятность рj его появления в
независимом опыте. В этом случае вероятность появления при л независимых испытаний конкретной
последовательности исходов j0 , j1 , j2 ... равна произведению вероятностей
этих исходов:
Цепь Маркова является
простейшим обобщением рассмотренной схемы независимых испытаний, которое
заключается в допущении зависимости исхода любого испытания от исхода предыдущего
испытания. Отсюда следует, что для описания последовательности X0, x1, X2 ... как цепи Маркова надо задать
распределение вероятностей {рi} первого испытания Х0 и всем парам вида (j,k) сопоставлять условные
вероятности pjk. Вероятность появления
конкретной последовательности исходов j0, j1, j2, ..., jn с учетом указанного
допущения равна произведению условных вероятностей:
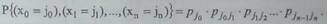
Еще одно обобщение
схемы независимых испытаний, приводящее к цепи Маркова, но несколько общего характера,
основывается на допущении, что исход любого испытания зависит не только от
исхода предыдущего испытания как такового, но и от порядкового номера
предыдущего испытания.
Итак, представим, что
цепь Маркова описывает некоторую систему с дискретными состояниями. Если система в
момент времени л, находилась в состоянии j, то вероятность перехода системы в
состояние k в момент времени п+ 1 зависит в общем
случае от значения n,j, k и не зависит от того, в каких
состояниях система пребывала в более ранний, чем л, момент времени.
Это свойство,
получившее название марковского, позволяет определить цепь Маркова через
условные вероятности рjk (п, п+1) того, что система
перейдет в состояние k в момент времени п+l, если она находилась в состоянии/ в момент времени п:
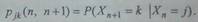
Если в момент времени и система находилась
в состоянии j, а в момент
времени п+т она перешла в состояние k, то говорят о переходе
системы из состояния j в состояние k за т шагов.
Вероятность такого перехода Pjk (п,п + т) называется т-шаговой переходной вероятностью.
Цепь Маркова является однородной, если
переходные вероятности не зависят от
времени. Для однородной цепи Маркова
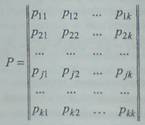
Данную матрицу называют матрицей вероятности перехода цепи
Маркова,
В этой матрице j-я строка( j=1,2...) представляет собой распределение вероятностей
случайной величины Хn+1, при условии, что Xn.=j. От-сюда следует, что сумма
вероятностей в каждой строке матрицы должна быть равна единице.
Таким
образом, матрица вероятностей перехода есть квадратная матрица с неотрицательными, не превышающими единицу
элементами, образующими по строкам
единичную сумму.
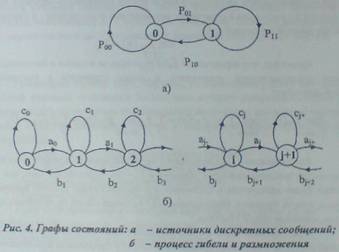
2.23. Примеры цепей Маркова
В теории информации
источники дискретных сообщений иногда рассматриваются как генераторы
последовательности символов из некоторого алфавита l={х1, х2, х3, ..., хn}. Если зависимость между
символами в последовательности простирается не более чем на пары соседних символов,
то такие последовательности являются цепями Маркова. Пусть алфавит состоит из L={0,1}, тогда сообщения
дискретного источника могут быть описаны матрицей:
где p00 и p11 - вероятности того, что
за принятым символом следует тот же самый, соответственно 0 или /; p10 и p01 — вероятности того, что
следующий символ будет отличен от принятого (0 или /).
С помощью цепей Маркова могут быть описаны
так называемые процессы гибели и
размножения, используемые в качестве моделей для исследования
численности популяций. Следуя этой модели, система находится в состоянии/ если число членов популяции равно/ Рождение одного члена популяции соответствует переходу системы
в состояние j + 1, а гибель одного члена популяции - переходу в
состояние j-1. В данной модели делается допущение, что сисnема за один шаг не
может перейти из состоя-ния j в состояние j +- k, если k>l.
При увеличении
численности популяции условия ее существования изменяются и, следовательно,
вероятности перехода системы из состоянья 7 в соседние состояния j + 1 и j - 1 будут зависеть в общем случае от/
Введем
обозначения для вероятностей перехода:
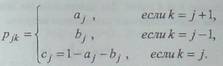
Состояние системы j=0 соответствует полному отсутствию членов популяции. Вероятность a0 рождения одного члена
популяции обычно
принимается больше нуля. С учетом
введенных обозначений матрица ве-роятностей перехода имеет вид
Процесс гибели и
размножения иногда исследуется при ограниче-нии на максимальную численность популяции
. Матрица вероятностей пе-перехода в этом случае становится конечной. Например, если по
достижении численности
популяции, равной четырем, размножение прекращается, процесс описывается матрицей
При исследовании цепей Маркова типичной задачей является опре-ление
вероятности того, что система, находящаяся в состоянии j, перей-
дет в состояние k за n шагов. Для однородных
(не зависит от времени) це-
пей Маркова задача
сводится к нахождению матрицы
Покажем, что для определения матрицы P(n) достаточно знать мат-
рицу
вероятностей перехода па один шаг Р = ||pjk||. Пустьсистема из со-
стояния j за n шагов переходит в
состояние k. Зафиксируем некоторый промежуточный момент времени s:
1=<s=<n-1.
Разобьем
движение системы на две части:
система
из состояния j переходит в состояние i за s шагов;
из состояния i система за n-s шагов переходит в
состояние k. На основании формулы полной вероятности рjk(п) будет равна:
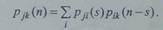
Отсюда ясно, что
вероятность перехода системы из состояния j в состояние k за n шагов pjk(n) есть элемент матрицы,
полученной как произведение матриц P(s) и P(n-s), т.е.
P(n) = P(s)P(n-s).
Последнее соотношение
называется уравнением Колмогорова-Чепмена, которое показывает, что матрица
переходных вероятностей за п шагов определяется произведением матрицы
переходных вероятностей за s шагов на матрицу
переходных вероятностей за n-s шагов.
Например:
- при п=2
и s=1, получаем
Р(2)=Р(1)Р(2-1) = Р2;
- при n=3 и s=2 -
Р(3) = Р(2)Р(3-2) = Р3;
- вообще для любого n -
Р(п) = Рn .
Два состояния системы будем называть смежными,
если возможен переход за один шаг из одного состояния в другое. Для
характеристики свойства смежности удобно вводить в рассмотрение на множестве
возможных состояний системы бинарное
отношение А, такое, что состояние Ak истинно, если pjk>0. В
этом случае возможен
формальный переход от матрицы вероятностей
перехода

к матрице смежности
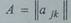
заменой элементов pjk элементами ajk по правилу:

Для наглядности матрицу смежности А представляют
также в виде графа состояний системы, в котором вершины соответствуют
состояниям системы, а дуги соединяют
вершины, соответствующие смежным состояниям, и указывают направления
перехода. При этом в качестве весов дуг естественно рассматривать вероятности
перехода в смежные состояния, а весам вершин
можно придать смысл вероятностей соответствующих состояний системы на n-m шаге.
На рис. 4 представлены графы состояний
рассмотренных систем.
Состояния i и j,
достижимые одно из другого, называют сообщающимися. Цепь Маркова называется
неприводимой, если ей соответствует единственный
класс сообщающихся состояний. Б противном случае цепь называется
приводимой. Если цепь Маркова состоит более чем из одного класса
сообщающихся состояний, она содержит, по крайней мере, одно собственное подмножество, являющееся замкнутым
множеством. Множество С называется замкнутым, если никакое состояние вне С
не может быть достигнуто ни из какого состояния, входящего в С. Если замкнутое j множество имеет
единственное состояние j, то оно называется поглощающим.
Очевидно,
что неприводимая цепь Маркова состоит из множества состояний, не содержащего
никакого другого собственного замкнутого подмножества Система, покинув однажды состояние j, может в общем случае через
некоторое число шагов возвратится в то же самое состояние, Пусть Pj(n) - вероятность того, что
первое возвращение в состояние j про-изойдет через л шагов. Тогда вероятность
того, что система вообще к либо возвратится в состояние у, определяется как сумма
вероятностей:
В
зависимости от того, какие значения принимает вероятное различают следующие состояния системы:
-
возвратное,
если Pj = 1;
-
невозвратное,
если и Рj < I.
Если
Pj=1, то состояние
системы классифицируется еще по среднему времени (среднему числу шагов между пребываниями в
состоянии j). Это
среднее время
возвращения:
Цепь Маркова называется эргодической, если все ее состояния эрго-дичны. Эргодическая
цепь Маркова обладает очень важным свойством -| при неограниченном
увеличении числа шагов вероятность перехода из состояния j в состояние k становится независимой
от
состояния j и стремится к предельной вероятности Uk:
lim pjk(n) = Uk
Очевидно,
что вероятности pjk (n) перехода
за п шагов в состояние при
неограниченном увеличении n также стремится
к предельным вероятностям:
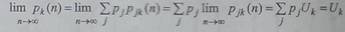
Распределение
{Uk } называется
стационарным распределением вероятностей эргодической цепи Маркина и Uk - это вероятность того,
что сис-тема будет находиться
в состоянии k в произвольный момент времени в отдаленном будущем. Нахождение {Uk} является одной из
основных задач исследования цепей Маркова.
При переходе цепи в
стационарный режим матрица переходных вероятностей
за п шагов превращается в матрицу предельных вероятностей;
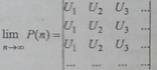
Один
из способов нахождения предельных вероятностей основан на использовании
соотношений p(n)=P^k.. При этом необходимо
возвести в достаточно высокую
степень матрицу вероятностей перехода Р. Однако этот метод достаточно трудоемок.
Другой способ основан на решении системы линейных
уравнений
где N - число состояний системы; рij — элемент матрицы вероятностей
перехода.
Можно показать, что
система линейных уравнений
|
является линейной зависимой; т.к. любое уравнение
системы выражается линейной
комбинацией N-1 остальных уравнений. Поэтому для дополнения данной системы до N независимых
уравнений используется условие
|
является линейной зависимой; т.к. любое
уравнение системы выражается линейной комбинацией N-1 остальных уравнений.
Поэтому для дополнения данной
системы до N независимых уравнений используется условие
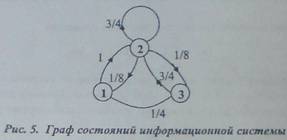
Рассмотрим пример цепи Маркова, описывающий
работу информационной системы, основными элементами которой являются оператор
и локальная сеть. С помощью персонального
компьютера оператор посылает данные с производственного участка в
информационно-вычислительный центр (ИВЦ).
Выделим три основных режима
работы системы:
- компьютер принимает сообщение из ИВЦ;
- компьютер находится в режиме ожидания;
- оператор передает сообщение.
Граф состояний информационной системы представлен
на рис. 5. В вершинах графа отражают
соответствующие состояния системы. Для этого примера задана матрица вероятностей перехода:

Из графа и матрицы
вероятностей перехода видно, что в режиме ожидания (состояние 2) система может остаться
в следующий (п+1)-й момент времени, если находилась в нем в n-й момент времени, с
вероятно-стью p22=3/4, либо перейти в режим
приема сообщений (состояние 1) с ве-роятностью p21=1/8, либо перейти в режим
передачи (состояние 3) с веро-
ятностью р23 1= 1/8. Из режима приема
сообщений система может перейти в режим ожидания, и этим обусловливается равенство
вероятности перехода p12 единице. Из режима передачи сообщений
система с вероятностью р32
=3/4 может перейти в режим ожидания с вероятностью p3 1 =1/4 в режим
приема.
Для определения таких важных характеристик системы, как среднее время занятости
оператора, среднее время простоя, необходимо знать ста-ционарное распределение вероятностей
{Uk }.
Составим систему
линейных уравнений:
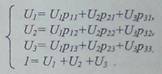
Представляя
значение вероятностей из матрицы вероятностей пере-хода P и решая эту систему,
получаем:
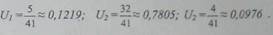
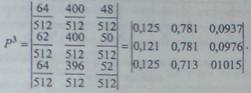
Рассмотрим второй
метод расчета стационарного режима. Для этого вычислим матрицы Р2 и Р3. Для
удобства сравнения матриц приведем их. элементы к общему знаменателю:
Из сравнения элементов матрица Р3 между собой и
с элементами матрицы-строки
U= |0,129
0,7805 0,0976|
находим, что значение вероятностей plk- p2k p3k мало отличаются друг
от друга и
от cooтветствующих
значений предельных вероятностей Uk (k=1,2,3), что
говорит о хорошей сходимости к их предельным значениям.
Такой процесс
относится к типу случайных процессов с дискретным
множеством возможных состояний L и непрерывным временным параметром
t e Т. В отличие от цепей Маркова дискретный
марковский процесс с непрерывным временем может переходитъ из состояния в состояние не в строго
фиксированные, а в любые моменты времени t. При этом предполагается, что
переходы осуществляются мгновенно (рис. 6).
На рис 6 изображена возможная реализация дискретного
случайного процесса с непрерывным временем, принимающего три возможных состояния (1.2.3}, Точками
на оси абсцисс отмечены моменты времени, соответствующие переходам процесса из
состояния в состояние. Эти моменты
заранее неизвестны, их
совокупность можно рассматривать как случайный поток событий.

Для исследования
дискретного марковского процесса с непрерывным временем может оказаться полезным
представление, связывающее каждое состояние процесса с отдельным управляющим
потоком случайных событий. Каждый поток может обладать своими собственными характеристиками.
Очередное событие, наступающее в j-м потоке, приводит процесс в некоторое
другое из возможных состояний лишь в том случае, если перед этим он находился в j-м состоянии; k- и поток переводит
поток из k-ro состояния и т.д.
Например, на рис. 6 моменты времени t2,t5 t7 t9 и т.д. есть
подмножество моментов времени, образующих управляющий поток, связанный с
состоянием 2.
Дискретный марковский
процесс с непрерывным временем налагает жесткие ограничения на характеристики
управляющих потоков. Эти ограничения диктуются марковским свойством.
Если обозначать
состояние процесса в момент времени t через X(t), то марковское
свойство заключается в следующем:
вероятность
pjk (t0, t)=P{X(t)=k|X(t0)=j} зависит только от t0 , t, j и k, т.е. вероятность того,
что процесс в некоторый момент времени t>t0 будет находиться в
состоянии k, зависит лишь от настоящего момента времени t0 и от состояния j, в котором процесс
находится в данный момент.
Следует обратить
внимание на то, что вероятность pjk(t0, t) не зависит от того,
как протекал процесс до момента времени t0 в частности, от того,
как долго
процесс находился в состоянии j до наступления момента време-
ни t0.
Время пребывания
процесса в некотором j-м состоянии Tj есть случайная величина, и
ясно, что она полностью определяется характеристиками управляющего потока. В
силу марковского свойства распределение остаточного времени Oj пребывания процесса в
состоянии у должно зависеть только от состояния j и не должно зависеть
от того, как долго процесс уже находился в состоянии j. Определимся с
требованиями к управляющему потоку.
Пусть случайная
величина Tj с плотностью распределения fj(t) есть время пребывания
марковского процесса в j-м состоянии. Рассмотрим поток случайных
событий Пj, интервалы между соседними событиями которого также
распределены по fj(t).
Реализацию подобного
потока можно получить из реализации суммарного потока (рис. 4), например для j=2, если составлять
интервалы между соседними событиями потока П2: из отрезков времени
длины [t2-t1],[t5 -t4,], [t7-t6], [t10-- t9], примыкающих
непосредственно друг к другу.
Предположим, что
началось наблюдение за марковским процессом с произвольного момента времени to, когда процесс
находился в состоянии j. Это эквивалентно тому, что на оси времени с изображенным на ней
потоком Пj случайным образом
отмечена точка t0 (рис. 7).
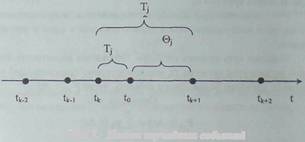
Рис. 7. Поток случайных событий
Точка t0 попадает на некоторый
интервал времени Tj*, являющийся случайной величиной.
Время до наступления следующего события в потоке Пj — случайная величина Оj — соответствует
остаточному времени пребывания марковского процесса в состоянии j. Управляющий j-й поток должен обладать такими
характеристиками, чтобы обусловленное его существованием время пребывания системы в
j-м состоянии Tj и остаточное время пребывания в том же состоянии Oj подчинялось одному и
тому же
закону распределения,
т.е. если gj(0) - плотность
распределения Oj, то при любых t=O выполняется равенство gj(O)=fj(t).
Существует доказательство, что для того чтобы остаточное
время
пребывания марковского процесса с непрерывным временем в
j-м состоя-
нии не зависело от того, сколько времени процесс уже
пребывал в этом со-
стоянии
время пребывания процесса в j-м состоянии
должно подчиниться
показательному закону распределения. Такой поток
называется пуассонов-
ским:
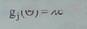
Пуассоновский поток
отличается от других потоков случайных событий двумя свойствами:
свойство отсутствия
последствия заключается в том, что моменты поступления событий на некотором
интервале времени [to, t] не зависят от того, в
какие моменты времени появлялись события в прошлом, т.е. до момента
времени ад
свойство ординарности
заключается
в принципиальной невозможности наступления более одного события в один и тот же момент времени.
Поясним суть второго
свойства. Обозначим вероятность того, что за малый промежуток времени At, непосредственно
примыкающий к моменту времени t, поступит более одного события, через Р>1(1,
/\t).
Очевидно, что
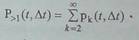
где рk (t, /\t) - вероятность появления
в интервале At ровно k событий. Ординарным называется
поток, для которого
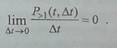
Одной из главных характеристик пуассоновского потока является его интенсивность - среднее число событий,
поступающих в интервале времени [t, t+/\t] при /\t -> 0:
Для ординарного
потока вторая составляющая правой части равенства обращается в нуль при /\t -> 0. Таким
образом, интенсивность пуассоновского потока равна

Пуассоновский поток
называется стационарным или простейшим, если его интенсивность - постоянная
величина: а(t)=a
Одной из центральных
задач при исследовании потоков случайных событий является нахождение
вероятности появления ровно k событий в данном
интервале времени [t0. t]. Для простейшего
потока эта вероятность не зависит от начального момента времени tо, а зависит лишь от
длины интервала
Т = t - tо.
Существует
доказательство того, что вероятность рk(Т) рассчитывается по формуле
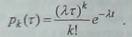
Определим закон
распределения интервала времени между двумя соседними событиями в простейшем потоке. При k=0 получаем вероятность того, что на
отрезке времени т не появится ни одного события, т.е.
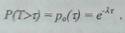
По определению,
функция распределения F(T) случайной величины Т (Т - интервал времени между
двумя соседними событиями в потоке) -есть вероятность Р(Т<T). Отсюда
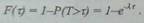
Дифференцируя последнее выражение, получаем плотность распределения случайной
величины T: