Энтропия. Формула Шеннона
Рассмотрим статический опыт, имеющий k равновероятных исходов. Таблица вероятностей такого опыта имеет следующий вид.
|
Исходы опыта |
А1 |
А2 |
А3 |
… |
Аk |
|
Вероятности |
1/k |
1/k |
1/k |
… |
1/k |
Общая неопределенность этого опыта может быть оценена величиной
log k .
Каждый
отдельный исход, имеющий вероятность 1/k, вносит
неопределенность, равную 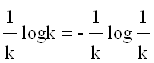 .
.
В том случае, если исходы имеют различную вероятность, (см. таблицу вероятностей),
|
Исходы опыта |
А1 |
А2 |
А3 |
|
Вероятности |
1/2 |
1/3 |
1/6 |
то исходы А1, А2, А3 вносят соответственно неопределенность равную:
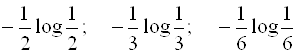 .
.
В случае независимости исходов общая неопределенность опыта будет равна:
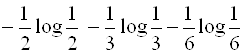 .
.
Обобщая рассмотрение вышеизложенного можно для опыта α с таблицей вероятностей
|
Исходы опыта |
А1 |
А2 |
… |
Аk |
|
Вероятности |
p (А1) |
p (А2) |
… |
p (Аk) |
сделать оценку в виде
![]()
В результате для опыта α мы получаем число, являющееся количественной мерой неопределенности опыта. Эта величина называется энтропией, а формула Шеннона для расчета энтропии имеет вид:
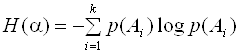 .
.
Свойства энтропии
1. Энтропия не может принимать отрицательных значений:
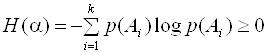 .
.
Это несложно доказать, т.к. 0£р(А)£1, а в этом интервале функция
log p(A) всегда отрицательна.
2. Энтропия H(α) равна 0 только в том случае, когда одна из вероятностей р(А1), р(А2),… р(Аk) равна единице, а все остальное равно 0.
Это становится очевидным, так как р(А1) + р(А2) + … + р(Аk) = 1, и согласно физическому смыслу, нулевое значение энтропии возможно только в том случае, когда опыт не содержит никакой неопределенности.
3. Среди всех опытов, имеющих k исходов, наиболее неопределенным является опыт с таблицей вероятности (см.таблицу),
|
Исходы опыта |
А1 |
А2 |
… |
Аk |
|
Вероятности |
1/k |
1/k |
… |
1/k |
который принято обозначать за опыт α0. В этом случае предсказать исход опыта труднее всего. Этому отвечает то обстоятельство, что опыт α0 имеет наибольшую энтропию. Данное свойство довольно часто используется, а его доказательство очень громоздкое, поэтому ограничивается утверждением: если α – произвольный опыт, имеющий k исхода (А1, А2, А3,,…, Аk,), то
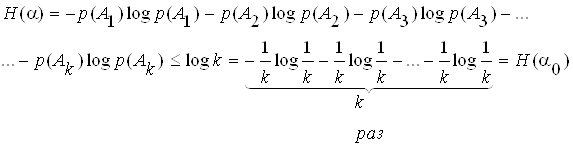
Рассмотрим пример по непосредственному использованию энтропии для количественной оценки неопределенности опыта. Предположим, что имеются две урны, содержащие по 20 шаров. В первой находится 10 белых, 5 черных и 5 красных. Во второй 8 белых, 8 черных и 4 красных. Из каждой урны вытаскивают по одному шару. Исход какого из двух опытов следует считать более неопределенным?
Обозначим за опыт α1 извлечение шаров из 1-й урны
|
Исходы опыта |
Б |
Ч |
К |
|
Вероятности |
1/2 |
1/4 |
1/4 |
Опыт α2 имеет свою таблицу вероятностей:
|
Исходы опыта |
Б |
Ч |
К |
|
Вероятности |
2/5 |
2/5 |
1/5 |
Значения энтропии опытов α1и α2:
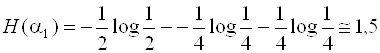 бит
бит
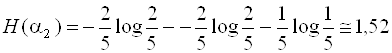 бит
бит
Следовательно, исход второго опыта содержит большую неопределенность.
Энтропия сложных событий
Если требуется оценить меру неопределенности сложных опытов, состоящих из целой совокупности следующих друг за другом испытаний, то необходимо иметь правило сложения энтропии. Допустим мы осуществляем два независимых опыта α.и β с таблицами вероятностей:
Опыт α
|
Исходы опыта |
А1 |
А2 |
… |
Аk |
|
Вероятности |
p(А1) |
p(А2) |
… |
р(Аk) |
Опыт β
|
Исходы опыта |
В1 |
В2 |
… |
Вl |
|
Вероятности |
p(В1) |
p(В2) |
… |
р(Вl) |
Рассмотрим сложный опыт αβ, состоящий в том, что одновременно осуществляются опыты α и β. Этот опыт имеет kl исходов:
A1B1, A2B2,
…, A1Bl; A2B1, A2B2,
…, A2Bl; AkB1, AkB2,
…, AkBl.![]()
В результате математических преобразований можно получить равенство
Н(αβ) = Н(α.) + Н(β).
Это равенство называется правилом сложения энтропии независимых опытов.
Если отказаться от условий независимости опытов α и β, то мы придем к понятно условной энтропии.
При этих условиях энтропия сложного опыта αβ не будет равна сумме энтропии α и β. Например, в случае если опыт αβ состоит в последовательном извлечении шаров из урны, содержащей всего два разноцветных шара. В этом случае после выполнения опыта α опыт β уже не будет содержать никакой информации и энтропия сложного опыта αβ будет равна энтропии одного опыта α, а не сумме энтропии опыта α. и β.
Условной энтропией опыта β при условии выполнения опыта α или условной энтропии опыта α при условии выполнения опыта β считается соответственно Нα(β) и Нβ(α):
Нα(β) = р(А1)НА1(β)+р(А2) НА2(β)+ ….+ р(Аk)НАk(β),
где НАk(β) – условная энтропия опыта β при условии Аk.
Таким образом, формула для подсчета энтропии Н(αβ) сложного опыта α β, в случае зависимости опытов α и β, имеет вид
Н(αβ)=Н(α)+Нα(β).
Данное выражение называется правилом сложения энтропии для зависимых опытов.
Свойства условной энтропии
1. Очень существенно, что условная энтропия Нα(β) заключается между нулем и энтропией Н(β) (безусловной):
![]() .
.
Это свойство хорошо согласуется со смыслом энтропии как меры неопределенности. Очевидно, что предварительное выполнение опыта α может лишь уменьшить степень неопределенности β, а в случае независимости опытов α и β степень неопределенности не изменится. Однако опыт α не может увеличить неопределенность опыта β.
То, что Нα(β) неотрицательное число очевидно из следующих соображений. Если все вероятности р(А1), р(А2), …, р(Аk) отличны от нуля, т.е. если опыт α. имеет действительно k исходов, то Нα(β)=0 в том и только в том случае, если НА1(β)=НА2(β)=…=НАk(β)=0, т.е. при любом исходе опыта α результат опыта β становится полностью определенным. При этом мы имеем Н(αβ)= Н(α). Если же опыты α и β являются независимыми, то
НА1(β)=НА2(β)=…=НАk(β)=Н(b), то Нα(β)=Н(β)
и энтропия сложного опыта переходит в известную:
Н(αβ) = Н(α)+Н(β).
2. Учитывая, что два сложных опыта αβ и βα не отличаются друг от друга, Н(αβ)=Н(βα).
Таким образом,
Н(α)+Нα(β)=Н(β)+Нβ(α).
Отсюда следует, что зная энтропии Н(α) , Н(β) и условную энтропию
Нβ(α), мы можем определить и условную энтропию:
Нβ(α)=Нa(β)+{Н(α)–Н(β)} .
Рассмотрим пример использования понятия условной энтропии для оценки конкретных ситуаций.
Известно, что некоторой болезнью в среднем болеют два человека из 100. Для выявления больных используется определенная прививка, реакция которой всегда оказывается положительной в том случае, когда человек болен. Если человек здоров, то она столь же часто бывает положительной, как и отрицательной.
Путь опыта β состоит в определении того, болен или здоров человек, а опыт α в определении результата указанной реакции.
Спрашивается, какова будет энтропия Н(β) опыта β и условная энтропия Нα(β) опыта β при условии осуществления α?
Очевидно, что здесь два исхода опыта β:
- исход В1 – человек здоров;
- исход В2 – человек болен.
Вероятности: р(В1)= 0,98, р(В2)= 0,02 ,
Н(β)= –0,98 log0,98 - 0,02 log0,02 » 0,14 бит.
Опыт α также имеет два исхода:
- исход А1 – положительная реакция;
- исход А2 – отрицательная реакция.
Вероятности: р(А1)=0,51, р(А2)=0,49, т.к. исход А1 имеет место в половине тех случаев, когда опыт β имеет исход В1 и во всех случаях, когда β имеет исход В2. Исход А2 имеет место лишь в половине случаев, когда β имеет исход А1.
Если опыт α имеет исход А1, то условные вероятности исходов β будут равны: pА1 (В1)=49/51; pА1(В2)=2/51, т.к. из 51 случая, в которых реакция оказалась положительной, в 49 случаях человек оказался здоров и только в 2 - больным.
Условная энтропия НА1(β) будет значительно больше Н(β):
 бит.
бит.
Если опыт a имел исход А2, то мы с уверенностью можем сказать, что опыт b имел исход B2 (человек болен). Следовательно, НА2(b)=0.
Таким образом, средняя условная энтропия опыта β при условии осуществления α будет равна:
Нα(β)=0,51´НА1(β)+0,49´НА2(β)=0,51´0,24=0,12 бит.
Следовательно, выполняя опыт α, мы уменьшаем степень неопределенности опыта β примерно на 0,02 бита.
Информация в сложном опыте
Рассмотрев основные понятия теории неопределенности, можно перейти к количественным оценкам такого фундаментального понятия как информация. Информация наряду с материей и энергией является первичным понятием нашего мира и поэтому в строгом смысле не может быть определена.
При энтропийной оценке степени неопределенности можно отметить, что равенство Н(β) нулю обозначает, что исход опыта β заранее известен. Большее или меньшее значение числа Н(β) соответствует большей или меньшей проблематичности результатов опыта.
Если наблюдение α, предшествует опыту β, то оно может изменить степень его неопределенности. Для того, чтобы результат измерения α мог сказаться на последующем опыте β, необходимо, чтобы этот результат был известен заранее. Поэтому α можно рассматривать как вспомогательный опыт, также имеющий несколько допустимых исходов.
Факт уменьшения неопределенности β при осуществлении опыта α находит свое отражение в величине Нα(β) – энтропии опыта β при условии выполнения опыта α. Очевидно, что Нα(β) не превосходит первоначальную энтропию Н(β) того же опыта. Можно также отметить:
- если опыт β не зависит от опыта α, то осуществление α не уменьшит энтропию Н(β) ;
- если результат опыта α полностью определит исход опыта β, то энтропия Н(β) уменьшится до нуля.
Таким образом, разность
I(α,β)=Н(β)–Нα(β)
указывает, на сколько осуществление опыта α уменьшает неопределенность опыта β. Величина I(α,β) называется количеством информации, и она означает как много нового мы узнаем об исходе опыта β, производя наблюдение α.
Такой подход к количественному определению информации представляется разумным ввиду того, что большинство измерений и других способов получения информации связано с введением условных понятий. Например: измеряя ток, мы следим за углом отклонения стрелки на приборе, измеряя температуру, мы следим за поведением ртути в термометре. Даже стоимость и количество товара мы оцениваем в рублях и т.д.
В некоторых случаях используют и более простые толкования понятий информации и соответственно расчетных формул.
Рассмотрим пример количественного расчета информации.
Пусть для некоторого пункта вероятность того что 15 июня будет идти дождь равна 0,4, вероятность того, что дождя не будет равна 0,6. Пусть далее для того же пункта вероятность дождя 15 октября равна 0,8, а отсутствие дождя - 0,2. Предположим, что определенный метод прогноза погоды 15 июня оказывается правильным в 3/5 всех тех случаях, в которых предсказывается дождь, и в 4/5 тех случаев, в которых предсказывается отсутствие осадков.
Применительно к погоде 15 октября этот метод оказывается правильным в 9/10 тех случаев, в которых предсказывается дождь, и в половине случаев, в которых предсказывается отсутствие дождя .
В какой из двух указанных дней прогноз дает больше информации о реальной погоде?
Обозначим через b1 и b2 опыты, состоящие в определении погоды в рассматриваемом пункте 15 июня и 15 октября.
Опыты имеют два исхода: В – дождь, ![]() - отсутствие осадков.
- отсутствие осадков.
Опыт b1
___
|
Исходы опыта |
В |
|
|
Вероятности |
0,4 |
0,6 |
Опыт b2
|
Исходы опыта |
В |
|
|
Вероятности |
0,8 |
0,2 |
Энтропии опытов b1 и b2 равны:
Н (b1) = –0,4´log 0,4 – 0,6´log 0,6 = 0,97 бит;
Н (b2) = –0,8´log0,2 – 0,8´log 0,8 = 0,72 бит.
Обозначим за α1 и α2 предсказания погоды на 15 июня и 15 октября.
Исходы А – дождь, ![]() –
отсутствие дождя
–
отсутствие дождя
Таблицы вероятностей пар опытов:
|
Пара (α1,β1) = |
|
|
|
|
|
0,6 |
0,4 |
0,2 |
0,8 |
|
Пара (α2,β2) = |
|
|
|
|
|
0,9 |
0,1 |
0,5 |
0,5 |
Учитываем, что pА(В)
+ pА(![]() ) = p
) = p![]() (В) + p
(В) + p![]() (
(![]() ) = 1.
) = 1.
Используя сумму полной вероятности, можно определить
неизвестные нам вероятности p1(А), p1(![]() ), p2(А) и p2(
), p2(А) и p2(![]() ) исходов А и
) исходов А и ![]() опытов α1 и α2.
Для опыта b1
опытов α1 и α2.
Для опыта b1
![]() .
.
Для опыта b2
![]() ,
,
так как p1(![]() ) = 1–p1(А),
p2(
) = 1–p1(А),
p2(![]() ) = 1– p2(А);
) = 1– p2(А);
p1(А) = p1(![]() ) = 0,5; p2(А) = 0,75; p2(
) = 0,5; p2(А) = 0,75; p2(![]() ) = 0,25.
) = 0,25.
Далее можно рассчитать условия энтропии опытов b1 и b2 при условии А и ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Следовательно, условие энтропии опытов b при условиях α выразится формулами:
![]() ;
;
![]() .
.
Таким образом, информация, содержащаяся в прогнозе погоды на 15 июля (опыт α1), о реальной погоде в этот день (b1) равна:
![]() бит ,
бит ,
а информация о реальной погоде 15 октября (опыт b2), содержащаяся в прогнозе на этот день (α2) будет определяться формулой
![]() бит.
бит.
Следовательно, прогноз на 15 июля более ценный, чем на 15 октября несмотря на то, что последний прогноз чаще оказывается правильным (по формуле полной вероятности).
На 15 июля
![]() .
.
На 15 октября
![]() .
.
Следует отметить, что подобный способ оценки качества любого прогноза уже самой своей универсальности не может охватить все аспекты вопроса. Он оперирует лишь вероятностями исходов. В некоторых случаях значительно важнее указать на один из исходов, например наводнение или землетрясение.
Свойства информации
1. Информация относительно опыта b, содержащаяся в опыте α, всегда равна информации относительно α, содержащейся в b.
Это непосредственно следует из соотношений:
Н(b) - Нα(b)=Н(α) - Нb(α).
Следовательно,
I(α,b) = Н(b) – Нα (b) = Н(α) – Нb(α) = I(b,α).
Таким образом, информацию I(α,b), которую содержит опыт α относительно b, можно назвать взаимной информацией двух опытов α и b относительно друг друга.
2. Информация I(α,b), содержащая в опыте α относительно опыта b, не превосходит энтропию Н(α) опыта α. Это свойство не требует доказательства, так как
I(α, b) = Н (α) – Нb (α).
3. Информация I(α,b) точно равна энтропии Н(α) только в том случае, когда условная энтропия Нb(α) точно равна нулю, т.е. результат опыта α, полностью определяет исход вспомогательного опыта b.
4. Если опыты α и b независимы, то информация I(α,b)=0
К более общим свойствам информации можно отнести следующие ее свойства:
1. Информация не материальна, но она проявляется в форме материальных носителей – дискетных знаков или символов.
2. Информация может быть заключена как в знаках, так и в их взаимном расположении.
3. Знаки и символы несут информацию только для получателя способного их распознать. Распознание состоит в соответствии знаков и символов с объектами и их отношениями в реальном мире. Поэтому информацию можно определить как результат моделирования реального мира.
Сигналами принято называть динамические процессы изменения во времени величины любой природы: тока, напряжения, излучения, звука и т.д.
Знаками будем называть различимые получателем реальные объекты: буквы, цифры, символы.
Избыточность в языке
При определении H1=H(a1) – энтропии опыта по оценке неопределенности, содержащейся в одной букве алфавита, мы считали, что буква независима. Это означает, что при составлении сообщения, в котором каждая буква содержит 4,35 бит информации, можно прибегнуть к помощи урны, в которой лежат тщательно перемешанные 1000 бумажек, из которых 175 не содержат ничего («пробел»), на 90 написана буква «О», на 72 – «Е» и т.д. Извлекая из такой урны бумажки, мы получим ничего не значащую фразу. Эта фраза будет похожа на русскую речь, но будет очень далека от разумного текста. Несходство полученной фразы с осмысленным сообщением объясняется тем, что на самом деле буквы в тексте не независимы друг от друга. Так, например, если мы знаем, что очередной буквой явилась гласная, то значительно возрастает вероятность появления на следующем месте согласной буквы и т.д.
Наличие в русском тексте определенных закономерностей приводит к дальнейшему уменьшению степени неопределенности одной буквы сообщения. Количественно это уменьшение можно оценить использованием условной энтропии H2 = Ha1(a2), которая является
энтропией опыта a2, состоящего в определении одной буквы текста при условии, что нам известен исход опыта a1, состоящего в определении предшествующей буквы.
Таким образом, особенности языка вносят определенную зависимость опытов, отражающихся в энтропии.
Известно, что с возрастанием числа букв в словах сообщения энтропия одной буквы уменьшается. К.Шенноном введено понятие избыточности языка:
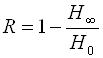 ,
,
где  – предельное значение энтропии с учетом
– предельное значение энтропии с учетом
вероятности сочетаний букв в словах сообщения, H0 – средняя неопределенность букв (в русском алфавите H0 = 4,35 бит).
Применительно к русскому языку избыточность заметно превышает 50 %. Это обстоятельство объясняется тем, что выбор следующей буквы осмысленного текста более, чем на 50 % определяется самой структурой языка и, следовательно, случаен лишь в сравнительно небольшой степени. Именно избыточность языка позволяет сокращать телеграфный текст за счет отбрасывания некоторых легко отгадываемых слов, предлогов, союзов. Она же позволяет легко восстанавливать истинный текст даже при наличии значительного числа ошибок в телеграмме или описок в книге.
???
Н = ![]() ,
где
,
где ![]() статистический опыт,
заключающийся в результате отгадывания буквы при условии, что нам известна
какой была предыдущая буква, т.е. нам известен результат предыдущего опыта
статистический опыт,
заключающийся в результате отгадывания буквы при условии, что нам известна
какой была предыдущая буква, т.е. нам известен результат предыдущего опыта ![]() 1.
1.
Код Шеннона-Фано
Идея использования неравенства H < log n для построения экономичного кода очень эффективно используется в кодах, которые впервые предложили в 1948 – 1949 гг. Р. Фано и К. Шеннон.
Предположим, что алфавит содержит n букв. Расположим буквы алфавита в один столбик в порядке убывания вероятностей. Затем разобьем их на две группы – верхнюю и нижнюю. Для букв первой группы в качестве первой цифры кодового обозначения используем 1, а для букв второй группы – цифру 0. Далее, каждую из двух полученных групп снова разделим на две части с возможно более близкой суммарной вероятностью. В качестве второй цифры кодового обозначения используются цифры 1 и 0 в зависимости от того, принадлежит ли буква к первой или второй из этих подгрупп. Затем каждая из содержащих более одной буквы групп снова делится на две части и т.д. Процесс повторяется до тех пор, пока каждая из разделенных групп будет содержать по одной букве.
Рассмотрим несложный принцип кодирования по методу Шеннона–Фано. Допустим, что алфавит содержит всего шесть букв, вероятности которых в порядке убывания равны 0,4; 0,2; 0,2; 0,1; 0,05; 0,05 (см. таблицу).
|
№ буквы |
Вероятность |
Группы |
Кодовое обозначение |
|
1 2 3 4 5 6
|
0,4 0,2 0,2 0,1 0,05 0,05 |
1 1 1 2 2 1 2 1 2 2 |
1 01 001 0001 00001 00000 |
Основной принцип, положенный в основу кодирования по методу Шеннона-Фано заключается в том, что при выборе каждой цифры кодового обозначения стараются, чтобы содержащаяся в ней информация была наибольшей. Разумеется, количество цифр в различных обозначениях будет неодинаковым, то есть код Шеннона-Фано является неравномерным. Буквы, имеющие большую вероятность, получают более короткие обозначения, чем соответствующие маловероятные буквы. В результате, хотя некоторые кодовые обозначения здесь и могут иметь весьма значительную длину, среднее значение длины такого обозначения значительно уменьшается.
Анализ экономичности кода
В нашем примере шестибуквенного алфавита равномерный код состоит из трехзначных кодовых обозначений ( так как 22 < 6 < 23 ). На каждую букву в лучшем случае приходится три сигнала. При использовании кода Шеннона-Фано среднее значение числа элементарных сигналов, приходящихся на одну букву сообщения, будет равно (данные берем из таблицы кодирования по методу Шеннона-Фано на с.45):
1´0,4 + 2´0,2 + 3´0,2 + 4´0,1 + 5´ (0,05 + 0,05) = 2,3 .
Это значительно меньше, чем 3, и не очень далеко от значения энтропии Н:
Н = –0,4´ log 0,4 – 2´0,2´ log 0,2 – 0,1´log 0,1 – 2´0,05´log 0,05 = 2,22.
Если провести аналогичный анализ для алфавита, состоящего из 18 букв, то равномерный код будет иметь пятизначное кодовое обозначение, а код Шеннона-Фано будет иметь буквы даже с семью двоичными сигналами, но зато среднее число элементарных сигналов, приходящихся на одну букву, будет равно 3,29 и это немного отличается от величины энтропии Н = 3,25. Особенно выгодно кодировать по методу Шеннона-Фано не отдельные буквы, а сразу целые блоки из нескольких букв. Даже в неблагоприятных случаях кодирование целыми блоками позволяет приближаться к величине энтропии. Рассмотрим пример, когда имеются лишь две буквы А и Б с вероятностями р(А) = 0,7 и р(Б) = 0,3.
Тогда Н = –0,7 log0,7 – 0,3 log0,3 = 0,881 .
Применение метода Шеннона-Фано к исходному двухбуквенному алфавиту здесь оказывается бесцельным. Он приводит нас к простейшему равномерному коду, требующему для передачи одного двоичного знака.
|
Буква |
Вероятность |
Кодовое обозначение |
|
А Б
|
0,7 0,3 |
1 0 |
Здесь мы имеем превышение Н на 12 %. Если применить код Шеннона-Фано к кодированию всевозможных буквенных сочетаний, то
|
Комбинация букв
|
Вероятность |
Кодовое обозначение |
|
АА АБ БА ББ
|
0,49 0,21 0,21 0,09 |
1 01 001 000 |
среднее значение длины кодового обозначения в этом случае
1´0,49 + 2´0,21 + 3´0,21 + 3´0,09 = 1,81 .
На одну букву приходится 1,81 / 2 = 0,905, что лишь на 3% больше
Н = 0,881 бит. При использовании трехбуквенных комбинаций средняя длина кодового обозначения 2,686, то есть на одну букву приходится 0,895 двоичных знаков, что всего на 1,5% больше Н.
Рассмотренные примеры анализа степени близости среднего числа двоичных знаков, приходящихся на одну букву сообщения, к значению Н может быть увеличено при помощи перехода к кодированию еще более длинных блоков. Этому обстоятельству посвящена основная теорема кодирования.
При кодировании сообщения, разбитого на N–буквенные блоки, можно, выбрав N достаточно большим, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близким к Н.
Анализ двоичной симметричной линии
Пусть по линии связи передается два элементарных сигнала (А1 – импульс, А2 – пауза). Вероятность безошибочного приема любого из передаваемых сигналов примем за 1–р, а вероятность ошибки будет равна р. В этом случае
рА1(А1) = рА2(А2) = 1–р, а рА1(А2) = рА2(А1) = р.
Графически схему двоичной симметричной линии принято изображать согласно схеме (рис.13). На рис.13, а отражена конфигурация передаваемого сигнала, а на рис.13,б показано, в какие принимаемые сигналы могут перейти передаваемые сигналы А1 и А2 и с какой вероятностью
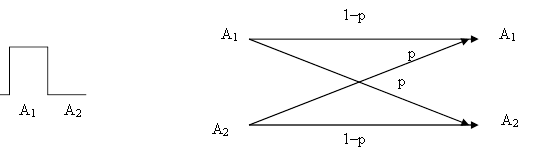 |
а) б)
Рис. 13. Схема двоичной симметричной линии: а - характер
сигналов А1 и А2; б - схема преобразования сигналов
Для вычисления величины с воспользуемся равенством
I(a, b) = H (b) – Ha (b) .
Из схемы (рис.13,б) видно, что если передается сигнал А1, то на приемном конце с вероятностью 1–р получим тот же сигнал А1, а с вероятностью р – сигнал А2. Аналогично с передачей сигнала А2. Потому
НА1(b) = НА2(b) = – (1–p) log (1–p) – p log p;
Ha (b) = p(A1) HA1(b) + p(A2) HA2(b) = – (1–p) log (1–p) – p log p,
так как р(А1) + р(А2) = 1.
Отсюда легко сделать вывод о том, что в рассматриваемом случае
Ha (b) не зависит от вероятностей р(А1) и р(А2), и для вычисления с = max I(a, b) = max[H (b) – Ha (b)] надо определить только максимальное значение H (b). Величина H (b) – энтропии опыта b, имеющего только два исхода (рис.13, а) и поэтому она не превосходит одного бита. Значение
H(b) = 1 достигается при р(А1) = р(А2) = 0,5, так как в этом случае оба исхода b будут равновероятными. В рассматриваемом случае р0(А1) =
= р0(А2) = 0,5,
с = 1 + (1–p) log (1–p) + p log p.
Следовательно, искомая пропускная способность двоичной симметричной линии будет равна
С = L[1 + (1–p) log (1–p) + p log p].
Последняя формула показывает, как пропускная способность двоичной симметричной линии зависит от вероятности ошибки р.
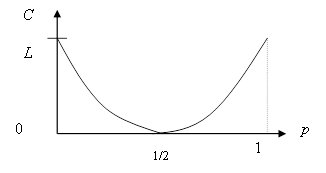 |
Рис. 14. Зависимость пропускной способности двоичной симметричной линии от вероятности ошибки
Наибольшее значение C = L функция достигает при р = 0 (помехи отсутствуют) и р = 1 (А1 ® А2, А2 ® А1) помеха не мешает понять какой сигнал был передан. При р = 0,5 пропускная способность линии равна нулю. Независимо от того, какой сигнал был передан, мы получим на приемном конце с вероятностью 0,5 сигнал А1 и с вероятностью 0,5 сигнал А2. Принятый сигнал не будет содержать никакой информации.