1. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. СЛУЧАЙНЫЕ СОБЫТИЯ И СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Когда мы говорим о получении информации о каком-то опыте или событии только в том случае, если мы заранее не знаем об их результате. В том же случае если мы заранее знаем исход того или иного события, то сообщение о том, что это произойдет, не несет нам никакой полезной информации (мы и так это знаем). То есть информация возникает из неопределенности и потенциально содержится только в случайных событиях или опытах.
Поэтому перед тем как перейти к изучению свойств и количественной оценки неопределенности случайных событий и информационного содержания, мы вспомним основные положения теории вероятностей.
Случайными называются опыты (испытания, наблюдения, процессы), дающие различные результаты в зависимости от обстоятельств, которые мы не знаем или не умеем учесть. Так, например, при бросании игральной кости мы не можем знать заранее, какая из граней окажется сверху, потому что это зависит от многих не известных нам обстоятельств.
При изучении явлений такого типа математика опирается на то, что при многократном повторении одного и того же опыта в одних и тех же условиях частота появления рассматриваемого результата (т.е. отношение числа опытов, при котором этот результат наблюдался, к общему числу производимых опытов) остается все время примерно одинаковой, близкой к некоторому постоянному числу р, т.е. вероятности появления результата.
Обычно, когда нет возможности проводить реальный опыт и оценивать частоту появления события, при нахождении вероятности руководствуются классическим ее определением: вероятность некоторого события равна отношению числа равновероятных исходов, благоприятных для данного события, к общему числу равновероятных исходов. То есть, определить вероятность появления события можно следующим образом:
p=m/n,
где m – число благоприятных исходов; n – общее число исходов.
Случайный опыт – представляет собой множество (полный набор) всех возможных исходов какого-нибудь случайного процесса. Например, процесс бросания игральной кости имеет 6 возможных исходов: 1, 2, 3, 4, 5 или 6.
Случайное событие – представляет собой некоторое подмножество множества исходов случайного опыта. Например, для бросания игральной кости событием может быть выпадение четного числа очков (исходы 2, 4, 6), числа очков кратных 3 (исходы 3 и 6) или случайным событием может быть просто выпадение какого-то конкретного числа, допустим числа 5. Из последнего примера видно, что случайное событие может совпадать с исходом (элементарное событие).
Вспомним нахождение среднего значения случайной величины. Случайная величина – это случайный опыт исходы, которого можно выразить в числовой форме (например, бросание игральной кости). В общем случае таблица вероятностей для случайной величины a имеет вид:
|
значения случайной величины |
а1 |
а2 |
… |
аk |
|
вероятности |
р1 |
р2 |
… |
рk |
Таким образом, среднее значение этой величины определяется формулой:
<a>=р1а1+р2а2+…+рkаk.
Задача №1
Пусть у нас есть ящик, в котором лежат тщательно перемешанные 10 шаров, отличающиеся друг от друга только цветом: 5 шаров белых, 3 черных и 2 красных. Вытащим не глядя из ящика один шар. Какова вероятность, что он будет того или другого цвета?
Решение:
В рассмотренной задаче №1 условие, что шары в ящике тщательно перемешаны и вынимаются не глядя, означает, что мы с равными основаниями можем ожидать появления любого из заключенных в ящике шаров или, другими словами, что извлечения всех шаров равновероятны. А так как шаров у нас было 10, то общее число возможных исходов m=10.
Далее, белых шаров у нас имеется 5, это соответствует числу благоприятных исходов для события, что мы извлечем белый шар. Поэтому вероятность вынуть белый шар равна 5/10 или 1/2. Рассуждая аналогично получаем, что вероятность извлечь черный шар составляет 0,3, а красный – 0,2.
Задача №2
Какова вероятность того, что при бросании игральной кости у нас выпадет число очков, кратное 3 ?
Решение: Р=2/6=1/3.
Задача №3
Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем были тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет окрашенных граней: а) одну; б) две; в) три.
Решение:
а) m=64*6=384, р=0,384; (только с одной стороны)
б) m=12*8=96? p=0,096; (ребра)
в) при m=8, р=0,008.
Задача №4
Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 3.
Решение: р=2/36=1/18.
Задача №5
Пусть таблицы вероятностей, указывающие частоту попаданий в мишень для двух стрелков А и В, имеют вид:
для стрелка А
|
число очков |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
вероятности |
0,02 |
0,03 |
0,05 |
0,1 |
0,15 |
0,2 |
0,2 |
0,1 |
0,07 |
0,05 |
0,03 |
для стрелка В
|
число очков |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
вероятности |
0,01 |
0,01 |
0,04 |
0,1 |
0,25 |
0,3 |
0,18 |
0,05 |
0,03 |
0,02 |
0,01 |
Кого из стрелков следует считать более метким?
Решение:
Для стрелка А=0,03+0,1+0,3+0,6+1+1,2+0,7+0,56+0,45+0,3=5,24.
Для стрелка В=0,01+0,08+0,3+1+1,5+1,08+0,35+0,24+0,18+0,1=4,84
4,84<5,24
2. СВОЙСТВА ВЕРОЯТНОСТИ. СЛОЖЕНИЕ И УМНОЖЕНИЕ СОБЫТИЙ. НЕСОВМЕСТИМЫЕ И НЕЗАВИСИМЫЕ СОБЫТИЯ
Вероятность р(А) любого события А есть правильная дробь (знаменатель больше числителя):
0 £ р(А) £ 1.
При этом вероятность может равняться 1 – это будет означать, что событие А осуществляется при любом исходе рассматриваемого опыта, т.е. что событие А достоверно. Вероятность может также равняться 0 – т.е. событие не осуществляется ни при каком исходе (событие невозможно).
Свойства вероятности.
1.
Если опыт имеет лишь два взаимно исключающих друг друга события А и В, то в
таком случае мы называем событие В противоположным событию А и обозначаем ![]() .
.
В этом случае справедливо свойство: ![]() .
.
2. Рассмотрим такие два события А и А1, что выполнение события А влечет за собой выполнение события А1 (например, А есть выпадение 6 при бросании игральной кости, а А1 – выпадение цифры, делящейся на 3). В таком случае событие А1 заведомо должно выполняться при всех тех исходах опыта, при которых выполняется событие А. Поэтому вероятность события А1 не может быть меньше вероятности события А. Таким образом получаем следующее свойство вероятностей:
если А Ì А1 («А подмножество А1»), то р(А) £ р(А1).
3. Если событие состоит в том, что выполняется хоть одно из каких-то двух событий А и В, то это событие называется суммой событий А и В и обозначается А+В. При этом могут иметь место два различных случая.
1) Если события А и В несовместимы, т.е. сразу оба они не могут иметь места, то
р(А+В)=р(А)+р(В).
В общем случае, если мы имеем k событий А1, А2,…, Аk никакие два из которых несовместны между собой. Тогда вероятность того, что выполнится хоть одно из этих событий:
р(А1+ А2+…+ Аk)= р(А1)+р(А2)+…+р(Аk).
Это правило сложения вероятностей.
Если опыт может иметь только n различных взаимоисключающих друг друга исходов, то ему соответствует таблица вероятностей:
|
А1 |
А2 |
… |
Аn |
|
р(А1) |
р(А2) |
… |
р(Аn) |
для которой справедлива сумма: р(А1)+р(А2)+…+р(Аn)=1.
2) Если события А и В совместимы, т.е. могут реализовываться одновременно, то в этом случае:
р(А+В)=р(А)+р(В)-р(АВ),
где АВ(произведение двух событий А и В) – это событие при котором выполняются оба события.
Нахождение вероятности произведения АВ событий довольно сложная задача. Однако есть частный случай, когда нахождение АВ не составляет труда.
4. Пусть события А и В независимые, т.е. результат опыта, с которым связано выполнение события А, никак не отражается на условиях опыта с результатом которого связано событие В. В этом случае:
р(АВ)=р(А)р(В).
Для k взаимно независимых событий А1, А2,…, Аk это правило имеет следующий вид:
р(А1А2…Аk)= р(А1)р(А2)…р(Аk).
Если события А и В не независимы, то правило умножения не обязано выполняться.
Это правило умножения вероятностей.
Задача №1
В колоде 52 карты. Одна из четырех мастей объявляется «козырной». Какова вероятность того, что взятая наудачу карта является тузом или козырем?
Решение:
А – событие, что выбранная карта туз, а В – карта является козырем. В таком случае событие АВ состоит в том, что эта карта является козырным тузом.
р(А)=1/13; р(В)=1/4; р(АВ)=1/52.
Значит:
р(А+В)=р(А)+р(В)-р(АВ)=1/13+1/4-1/52=4/13.
Задача №2
В цехе установлены два станка, производящие одинаковые изделия. Из опыта известно, что 1-й станок может произвести в сутки до 3-х бракованных изделий, причем вероятности бракованных изделий таковы:
|
Число брак. изделий (в сутки) |
0 |
1 |
2 |
3 |
|
вероятности |
0,3 |
0,4 |
0,2 |
0,1 |
2-й станок производит не более одного бракованного изделия в сутки, причем вероятности брака такова:
|
Число брак. изделий (в сутки) |
0 |
1 |
|
вероятности |
0,9 |
0,1 |
Построить таблицу вероятностей брака производимого обоими станками одновременно. Определить, среднее число произведенных цехом в сутки бракованных изделий.
Решение:
Рассмотрим две случайные величины a (первый станок) и b (второй станок).
<a>=0,3*0+0,4*1+0,2*2+0,1*3=1,1.
<b>=0,9*0+0,1*1=0,1.
Нас же интересует случайная величина <a+b>. Случайные величины a и b независимые. Т.е. a принимает значения 0,1,2,3 с соответствующими вероятностями независимо от того какое значение принимает b.
Строим таблицу вероятностей брака для обоих станков.
|
значения |
0+0 |
0+1 |
1+0 |
1+1 |
2+0 |
2+1 |
3+0 |
3+1 |
|
вероятности |
0,3*0,9 |
0,3*0,1 |
0,4*0,9 |
0,4*0,1 |
0,2*0,9 |
0,2*0,1 |
0,1*0,9 |
0,1*0,1 |
|
значения |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
|
вероятности |
0,27 |
0,03 |
0,36 |
0,04 |
0,18 |
0,02 |
0,09 |
0,01 |
|
значения |
0 |
1 |
2 |
3 |
4 |
|
вероятности |
0,27 |
0,39 |
0,22 |
0,11 |
0,01 |
Теперь по формуле для среднего значения случайной величины находим среднее число произведенных цехом в сутки бракованных изделий:
<a+b>=0,27*0+0,39*1+0,22*2+0,11*3+0,01*4=1,2.
Видно, что среднее значение суммы двух случайных величин равно сумме их средних значений.
Задача №3
Два стрелка стреляют одновременно по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.
Решение:
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
Задача №4
Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.
Решение:
![]()
Задача №5
Шесть охотников увидели лису и одновременно выстрелили в нее. Предположим, что каждый из охотников на таком расстоянии обычно попадает в лису и убивает ее в одном случае из трех. Какова вероятность того, что лиса будет убита?
Решение:
Пусть события А1, А2,…,А6 означают поражение лисы 1,2,…,6-м охотниками. Из условия задачи нам известно, что Р(А1)=р(А)=…=р(А6)=1/3.
Требуется найти вероятность р(S), где S= А1+А2+…+А6. События А1, А2,…,А6, очевидно независимые и совместные; поэтому при решении этой задачи нужно воспользоваться формулой сложения вероятностей независимых совместных событий:
р(А+В)=р(А)+р(В)-р(АВ)= р(А)+р(В)-р(А)р(В).
Однако формула,
выражающая вероятность суммы многих (совместимых) событий довольно сложна.
Поэтому, будем искать вероятность того, что лиса уцелеет, т.е. ![]() . Промах охотников обозначим через
. Промах охотников обозначим через ![]() ,
,![]() ,…,
,…,![]() .
.
![]()
Чтобы лиса
уцелела, необходимо, чтобы все охотники промахнулись, т.е. здесь речь идет о
вероятности события ![]() , где события
, где события ![]() ,
,![]() ,…,
,…,![]() - взаимно независимые. Итак
- взаимно независимые. Итак
![]()
Тогда: р(S)=1-64/729=665/729.
Задача №6
Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятность того, что нужная деталь содержится: а) не более чем в трех ящиках; б) не менее чем в двух ящиках.
Решение:
а) Проще найти вероятность противоположного события, что нужная деталь находится больше чем в 3 ящиках (т.е. в 4):
![]() ;
; ![]() .
.
б) Найдем, что нужная деталь находится меньше чем в 2 (т.е. в одном или ни в одном):
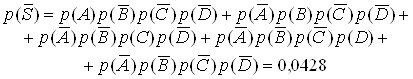
Получаем: ![]()
3. УСЛОВНЫЕ ВЕРОЯТНОСТИ
Два события А и В мы называли независимыми, если результат опыта, с которым связано событие А, не влияет на условия опыта, с которым связано событие В. Однако это обстоятельство не всегда имеет место.
В том случае, если опыт, с которым связано событие В, зависит от результата опыта, с которым связано событие А, то:
![]() .
.
Это общее правило для определения вероятности произведения АВ двух событий. Его также часто называют правилом умножения вероятностей.
Так как события АВ и ВА не отличаются, то из последней формулы получаем:
![]() ,
,
Отсюда получаем формулу Бейеса:
![]() .
.
Отметим, что поскольку одно из событий А и ![]() обязательно имеет место, то сумма
событий АВ и
обязательно имеет место, то сумма
событий АВ и ![]() В совпадает с событием В. А так как
В совпадает с событием В. А так как ![]() ,
, ![]() и
и ![]() (события АВ и
(события АВ и ![]() В не совместимы, т.к. несовместимы А
и
В не совместимы, т.к. несовместимы А
и ![]() ), то:
), то:
![]() .
.
Совершенно аналогично, если какой-либо опыт a может иметь k (и только k) попарно несовместимых исходов А1 , А2, …, Аk, то любое событие В можно представить в виде суммы событий А1В+А2В+ …+АkВ и
![]() .
.
Это формула полной вероятности.
Задача №1
Слово «папаха» составлено из букв разрезанной азбуки. Затем карточки с буквами тщательно перемешиваются и из них извлекаются по очереди и раскладываются в ряд какие-то четыре. Какова вероятность получить таким путем слово «папа»?
Решение:
Событие А – первой извлекается буква «п», событие В – второй окажется буква «а», С – третьей окажется буква «п», D – четвертой окажется буква «а». В таком случае, событие, вероятность которого нас интересует, можно записать как АВСD. Далее применяя последовательно несколько раз формулу для вероятности произведения двух событий, получим:
![]() ;
;
![]() ;
;
![]() ;
;
и наконец получаем
![]() .
.
Задача №2
Имеется 5 урн, из которых две содержат по одному белому и по 5 черных шаров, одна урна – 2 белых и 5 черных шаров и последние две урны – по 3 белых и по 5 черных шаров. Наудачу выбирается одна урна и из нее наудачу извлекается один шар. Какова вероятность, что этот шар окажется белым?
Решение:
Обозначим через А1 , А2 и А3 события, состоящие в том, что шар извлечен из урны, содержащей 1, или 2, или 3 белых шара . В таком случае:
![]() ,
, ![]() ,
,![]() .
.
Если событие В состоит в том, что извлекается белый шар, то по формуле полной вероятности, получаем:
![]()
![]() .
.
Задача №3
В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновероятны все возможные предположения о первоначальном составе шаров (цвете).
Решение:
Событие В – извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: А1 – белых шаров нет, А2 – один белый шар, А3 –два белых шара. Так как, всего имеется три равновероятные гипотезы, то вероятность каждой гипотезы равна 1/3, т.е. Р(А1)= Р(А2) =Р(А3)=1/3.
Тогда: РА1(В)=1/3; РА2(В)=2/3; РА3(В)=1.
Получаем: Р(В)= Р(А1)РА1(В)+Р(А2) РА2(В)+Р(А3)РА3(В)=2/3.
Задача №4
В вычислительной лаборатории имеются шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на случайно выбранной машине. Найти: 1) вероятность того, что до окончания расчета машина не выйдет из строя; 2) вероятность того, что студент работал на той или иной машине, если она не вышла из строя?
Решение:
Событие В – машина не выйдет из строя.
А1 – расчет ведется на автомате, А2 – расчет ведется на полуавтомате.
Р(А1)=0,6 ; Р(А2)=0,4.
Из условия задачи известно: РА1 (В)=0,95, РА2 (В)=0,8.
Получаем: Р(В)= 0,6*0,95+0,4*0,8=0,89.
Найдем
теперь условные вероятности ![]() и
и ![]() . Для этого используем формулу
Бейеса:
. Для этого используем формулу
Бейеса:
![]() ,
, ![]() .
.
Задача №5
В первой урне содержится 10 шаров, из них 8 белых и 2 черных; во второй урне 20 шаров, из них 4 белых и 16 черных. Из каждой урны наудачу извлекли по одному шар, а затем из этих двух шаров наудачу был взят один шар. Найти вероятность того, что взят белый шар.
Решение:
А1 – комбинация шаров Б:Б; А2 – комбинация Ч:Б; А3 – Б:Ч; А4 – Ч:Ч.
Так как, мы имеем дело с независимыми событиями и они происходят одновременно, то:
Р(А1)=0,8*0,2=0,16; Р(А2)=0,2*0,2=0,04; Р(А3)=0,8*0,8=0,64; Р(А4)=0,2*0,8=0,16.
В – взятый один их двух шаров окажется белым:
РА1(В)=1; РА2(В)=0,5; РА3(В)=0,5; РА4(В)=0.
По формуле полной вероятности, находим:
Р(F)=0,16*1+0,04*0,5+0,64*0,5+0,16*0=0,5.
4. МАРКОВСКИЕ ПРОЦЕССЫ
Марковские
процессы являются разновидностью дискретных случайных процессов. Пространство
состояний дискретного Марковского процесса представляет собой конечное или счетное
множество, которое часто отождествляют с множеством неотрицательных целых чисел
![]() или
или ![]() .
Особенностью Марковских процессов является то, что вероятность перехода системы
в другое состояние в следующий момент времени зависит только от того в каком
состоянии процесс находится в данный момент времени и от того времени, сколько
он в нем находится.
.
Особенностью Марковских процессов является то, что вероятность перехода системы
в другое состояние в следующий момент времени зависит только от того в каком
состоянии процесс находится в данный момент времени и от того времени, сколько
он в нем находится.
4.1. Цепи Маркова
Цепью
Маркова является дискретный Марковский процесс с дискретным временем. Он
характеризуется тем, что переход от состояния к состоянию возможен лишь в
дискретные моменты времени ![]() . При этом
абсолютные значения моментов времени не играют роли, поэтому часто время
отождествляется с множеством индексов
. При этом
абсолютные значения моментов времени не играют роли, поэтому часто время
отождествляется с множеством индексов ![]() и
тогда цепь Маркова имеет вид:
и
тогда цепь Маркова имеет вид:
![]() ,
,
где ![]() -
случайная величина, принимающая значения из множества
-
случайная величина, принимающая значения из множества ![]() ,
,
![]() - момент времени.
- момент времени.
Однородные цепи Маркова, в которых вероятности перехода не зависят от времени, удобно описывать матрицей одношаговых переходных вероятностей:
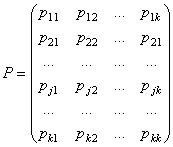 ,
,
здесь ![]() -
вероятность перехода из состояния
-
вероятность перехода из состояния ![]() в состояние
в состояние ![]() за один шаг.
за один шаг.
Кроме того, очень часто для наглядности цепи Маркова представляют графически с помощью ориентированных взвешенных графов.
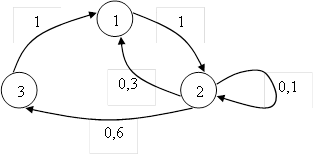
Вершины графа представляют собой состояния системы, а дуги показывают возможные переходы из одного состояния в другое. Приписываемые дугам весовые коэффициенты характеризуют переходные вероятности.
Эргодическая
цепь Маркова обладает очень важным свойством – при неограниченном
увеличении числа шагов вероятность ![]() перехода из
состояния
перехода из
состояния ![]() в состояние
в состояние ![]() становится независимой от состояния
становится независимой от состояния ![]() и стремится к предельной вероятности
и стремится к предельной вероятности
![]() . Распределение
. Распределение ![]() называется стационарным
распределением вероятностей эргодической цепи Маркова и
называется стационарным
распределением вероятностей эргодической цепи Маркова и ![]() - это вероятность того, что система
будет находиться в состоянии
- это вероятность того, что система
будет находиться в состоянии ![]() в отдаленном
будущем.
в отдаленном
будущем.
Один из
способов нахождения предельных вероятностей основан на возведении в достаточно
высокую степень матрицу одношаговых вероятностей перехода ![]() . Однако этот способ трудоемок и не
всегда приемлем. Другой способ основан на решении системы линейных уравнений:
. Однако этот способ трудоемок и не
всегда приемлем. Другой способ основан на решении системы линейных уравнений:
 ,
,
где ![]() -
число состояний системы,
-
число состояний системы, ![]() - элемент матрицы
одношаговых вероятностей перехода.
- элемент матрицы
одношаговых вероятностей перехода.
Задача №1.
Процесс движения частицы под действием случайных сил представлен
в виде цепи Маркова. Движение рассматриваем по числовой оси ![]() внутри отрезка
внутри отрезка ![]() . Частица может перемещаться
внутри данного отрезка на величину
. Частица может перемещаться
внутри данного отрезка на величину ![]() вправо (с
вероятностью
вправо (с
вероятностью ![]() ) или влево (с вероятностью
) или влево (с вероятностью ![]() ). По достижении частицей
одной из границ (
). По достижении частицей
одной из границ (![]() или
или ![]() ) частица полностью отражается от них
(случайное блуждание с отражающими экранами). Считая
) частица полностью отражается от них
(случайное блуждание с отражающими экранами). Считая ![]() ,
,
![]() , представить модель данного процесса
направленным графом и матрицей переходных вероятностей.
, представить модель данного процесса
направленным графом и матрицей переходных вероятностей.
Решение:
Состояние частицы определяется ее положением на оси ![]() , т.е. множество состояний представляет
собой
, т.е. множество состояний представляет
собой ![]() . Представим граф, характеризующий
данный процесс.
. Представим граф, характеризующий
данный процесс.
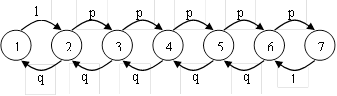
Матрица вероятностей перехода для данного процесса имеет вид:

Задача №2.
Процесс
движения частицы под действием случайных сил представлен в виде цепи Маркова.
Движение частицы рассматриваем по числовой оси ![]() внутри
отрезка
внутри
отрезка ![]() . Частица перемещается внутри
данного отрезка на величину
. Частица перемещается внутри
данного отрезка на величину ![]() вправо (с
вероятностью
вправо (с
вероятностью ![]() ) или влево (с вероятностью
) или влево (с вероятностью ![]() ). По достижении частицей
одной из границ (
). По достижении частицей
одной из границ (![]() или
или ![]() ):
):
1) частица прекращает свое движение (случайное блуждание с поглощающими экранами);
2) частица с
вероятностью ![]() отражается в соседнее состояние и с
вероятностью
отражается в соседнее состояние и с
вероятностью ![]() остается в крайних состояниях
(случайное блуждание с полуотражающими экранами).
остается в крайних состояниях
(случайное блуждание с полуотражающими экранами).
Считая ![]() ,
, ![]() ,
представить модель процесса движения частицы для первого и второго случая
направленным графом и матрицей переходных вероятностей.
,
представить модель процесса движения частицы для первого и второго случая
направленным графом и матрицей переходных вероятностей.
Решение:
1) Построим граф для данного процесса
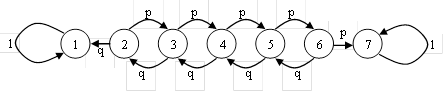
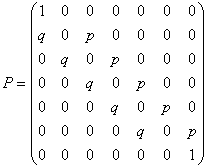
2) Граф, характеризующий данный процесс, имеет вид


Задача №3.
Дан граф, характеризующий цепь Маркова
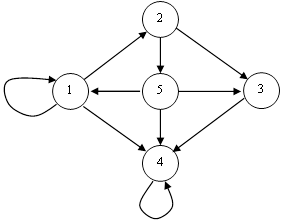
Для приведенного графа построить матрицы: смежности (А), достижимостей (R), контрдостижимостей (Q) и взаимодостижимостей (H). Установить приводимая ли это цепь и построить конденсацию графа.
Решение:
Матрица смежностей A характеризует возможность перехода из одного состояния системы в другое за один шаг:
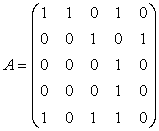
Матрица
достижимостей R показывает
возможность перехода из данного состояния в другое за конечное число шагов ![]() . R получим на основе матрицы смежности А, руководствуясь
простым алгоритмом:
. R получим на основе матрицы смежности А, руководствуясь
простым алгоритмом:
1) строим первую строку матрицы достижимостей R. Переписываем первую строку матрицы А;
2) отмечаем
любой элемент первой строки матрицы R, отличный
от нуля (например, ![]() ). Выбираем k-ю строку матрицы А и дополняем первую строку матрицы R соответствующими элементами этой
строки равными 1;
). Выбираем k-ю строку матрицы А и дополняем первую строку матрицы R соответствующими элементами этой
строки равными 1;
3) отмечаем любой неотмеченный элемент в первой строке матрицы R и возвращаемся к пункту 2. Процесс повторяем до тех пор, пока не останется неотмеченных элементов в первой строке матрицы R или пока вся строка не будет заполнена единицами. Далее переходим к аналогичному построению второй и последующих строк;
4) главную диагональ матрицы R заполняем единицами (если она еще не заполнена).
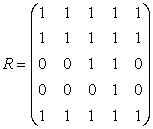
Матрица
контрдостижимостей Q характеризует
возможность попадания в данное состояние из других состояний системы за
конечное число шагов ![]() . Данную матрицу Q мы получаем путем транспонирования R:
. Данную матрицу Q мы получаем путем транспонирования R:

Матрица
взаимодостижимостей H показывает возможность
перехода из данного состояния в другое и наоборот за конечное число шагов ![]() . Данная матрица может быть получена
на основе матриц R и Q руководствуясь следующим принципом: если элементы с одинаковыми
индексами матриц R и Q
равны 1, то соответствующему элементу матрицы H
тоже присваиваем единицу, иначе – ноль.
. Данная матрица может быть получена
на основе матриц R и Q руководствуясь следующим принципом: если элементы с одинаковыми
индексами матриц R и Q
равны 1, то соответствующему элементу матрицы H
тоже присваиваем единицу, иначе – ноль.
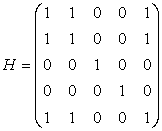
Из матрицы H мы заключаем, что данная цепь Маркова состоит из 3-х классов
сообщающихся состояний: ![]() ,
, ![]() ,
, ![]() .
Так как граф распадается на классы сообщающихся состояний, то цепь является
приводимой (в противном случае – неприводимой).
.
Так как граф распадается на классы сообщающихся состояний, то цепь является
приводимой (в противном случае – неприводимой).
Конденсация данного графа, т.е. граф, вершины которого есть классы сообщающихся состояний (максимально сильно связанные подграфы), имеет следующий вид:
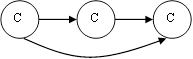
Задача №4.
Дан граф, характеризующий цепь Маркова
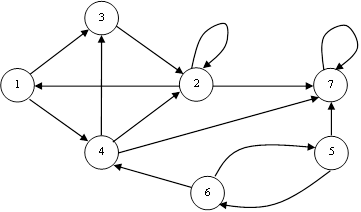
Для приведенного графа построить матрицы: смежности (А), достижимостей (R), контрдостижимостей (Q) и взаимодостижимостей (H). Установить приводимая ли это цепь и построить конденсацию графа.
Решение:
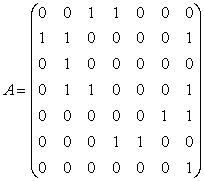
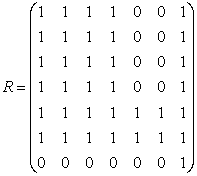

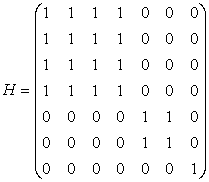
Из матрицы H мы заключаем, что данная цепь Маркова состоит из 3-х классов
сообщающихся состояний: ![]() ,
, ![]() ,
, ![]() .
Цепь является приводимой.
.
Цепь является приводимой.
Конденсация данного графа имеет следующий вид:
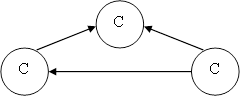
Задача №5.
Работа системы автоматического управления (САУ) описывается цепью Маркова и характеризуется следующим графом состояний
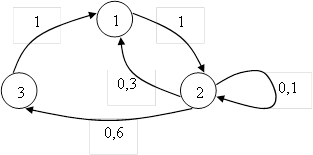
1 – измерение параметров объекта управления; 2 – обработка данных и принятие решения об управляющих воздействиях; 3 – исполнение решения. Вычислить чему равно среднее время измерения, обработки измеренной информации и управления объектом, за сутки работы САУ.
Решение:
Чтобы найти, сколько времени находится САУ в одном из трех состояний в течение суток, нужно определить значение предельных вероятностей данной системы.
Этому графу соответствует матрица одношаговых вероятностей перехода
 .
.
Для нахождения предельных вероятностей ![]() ,
, ![]() ,
, ![]() составим систему линейных уравнений:
составим систему линейных уравнений:

Решая эту
систему уравнений, получаем: ![]() ,
, ![]() ,
, ![]() .
.
Таким образом:
среднее
время измерения ![]() или 8ч38мин.
или 8ч38мин.
среднее
время обработки ![]() или 9ч 36мин.
или 9ч 36мин.
среднее
время управления ![]() или 5ч 46мин.
или 5ч 46мин.
4.2. Дискретный Марковский процесс с непрерывным временем
Дискретный Марковский процесс с непрерывным временем относится к типу случайных процессов с дискретным множеством возможных состояний и непрерывным временным параметром. Данный процесс может переходить из состояния в состояние не в строго фиксированные, а в любые моменты времени. Поток событий в данном процессе должен обладать следующими свойствами: 1) свойство отсутствия последействия – заключается в том, что наступление событий на некотором интервале времени не зависит от того, в какие моменты времени события появлялись в прошлом; 2) свойство ординарности – заключается в принципиальной невозможности наступления более одного события в один и тот же момент времени.
Этими
свойствами обладает только поток событий, в котором интервалы времени между
соседними событиями распределены по показательному закону: ![]() . Такие потоки называются Пуассоновскими.
. Такие потоки называются Пуассоновскими.
Предельные
вероятности ![]() состояний стационарного
режима дискретного Марковского процесса с непрерывным временем могут быть
найдены в результате решения системы линейных уравнений (полученных на
основании уравнений Колмогорова):
состояний стационарного
режима дискретного Марковского процесса с непрерывным временем могут быть
найдены в результате решения системы линейных уравнений (полученных на
основании уравнений Колмогорова):
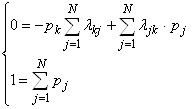 .
.
где ![]() –
интенсивность потока случайных событий, переводящего систему из состояния j в состояние k.
–
интенсивность потока случайных событий, переводящего систему из состояния j в состояние k.
Задача №1.
Информационная система описывается с помощью дискретного Марковского процесса с непрерывным временем и может быть представлена графом состояний
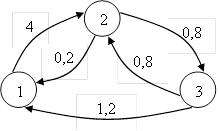
Найти предельные вероятности состояний системы.
Решение:
Составим
матрицу интенсивностей ![]() потоков случайных событий,
переводящих систему из состояния
потоков случайных событий,
переводящих систему из состояния ![]() в состояние
в состояние ![]() :
: 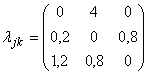 .
.
Составим систему линейных алгебраических уравнений, характеризующих стационарный режим функционирования данной информационной системы:
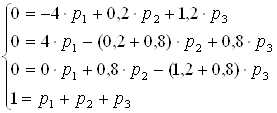
![]()
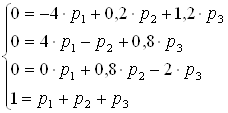
![]()
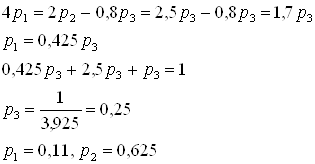
В
результате получаем: ![]() .
.
Задача №2.
Информационная система описывается с помощью дискретного Марковского процесса с непрерывным временем и может быть представлена графом состояний
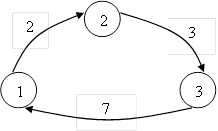
Найти стационарное распределение вероятностей состояний системы.
Решение:
Составим
матрицу интенсивностей ![]() потоков случайных событий,
переводящих систему из состояния
потоков случайных событий,
переводящих систему из состояния ![]() в состояние
в состояние ![]() :
: 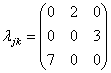 .
.
Составим систему линейных алгебраических уравнений, характеризующих стационарный режим функционирования данной информационной системы:
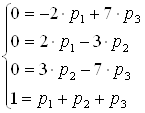


В
результате получаем: ![]() .
.
Задача №3.
Информационная система, описываемая с помощью дискретного Марковского процесса с непрерывным временем, может быть представлена графом состояний
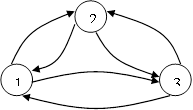
Найти стационарное распределение вероятностей состояний системы, если этому графу соответствует матрица условных переходных вероятностей
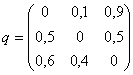 ,
,
а интенсивности потоков событий, связанных с 1,2 и 3 состояниями, соответственно равны:
![]() ,
, ![]() ,
, ![]() .
.
Решение:
Определим
интенсивности ![]() потоков случайных событий,
переводящих систему из состояния
потоков случайных событий,
переводящих систему из состояния ![]() в состояние
в состояние ![]() :
: ![]() ,
,
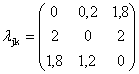 .
.
В результате взвешенный граф состояний данной информационной системы будет выглядеть следующим образом:
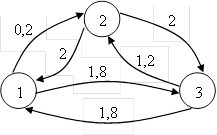
Составим систему линейных алгебраических уравнений, характеризующих стационарный режим функционирования данной информационной системы:
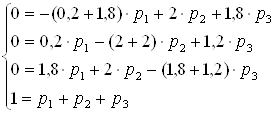
![]()

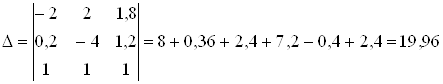
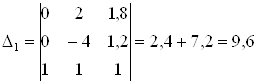
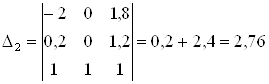
В
результате получаем: ![]() .
.
Задача №4.
Информационная система, представленная в виде цепи Маркова, имеет три состояния показанных на графе
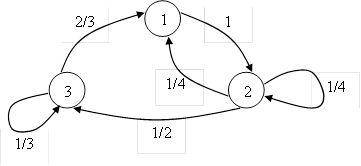
Перейти от модели описываемой цепью Маркова к Марковскому процессу с непрерывным временем. Построить граф, характеризующий систему как Марковский процесс с непрерывным временем, и найти предельные вероятности состояний.
Решение:
Чтобы
определить интенсивность потоков случайных событий ![]() ,
переводящих систему из состояния j в состояние k, надо получить
матрицу условных переходных вероятностей
,
переводящих систему из состояния j в состояние k, надо получить
матрицу условных переходных вероятностей ![]() для
Марковского процесса с непрерывным временем. При этом мы должны учитывать, что:
для
Марковского процесса с непрерывным временем. При этом мы должны учитывать, что:
1) ![]() ;
;
2) 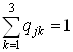 ;
;
3) пропорции между вероятностями перехода в цепи должны остаться справедливыми и для Марковского процесса с непрерывным временем.
Отсюда получаем:
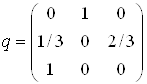
Определим
интенсивности ![]() потоков случайных событий,
переводящих систему из состояния
потоков случайных событий,
переводящих систему из состояния ![]() в состояние
в состояние ![]() :
:
![]() ,
,
![]() ,
,
где ![]() ,
Т – период дискретизации цепи Маркова.
,
Т – период дискретизации цепи Маркова.
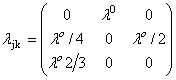
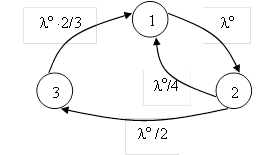
В результате граф состояний данной информационной системы будет выглядеть следующим образом:
Составим систему линейных алгебраических уравнений, характеризующих стационарный режим функционирования данной информационной системы:
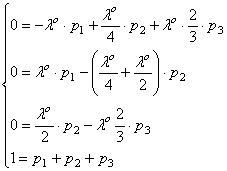
![]()
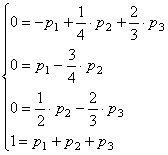
Получаем: ![]() .
.
5. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Процессами массового обслуживания являются процессы, составными элементами которых являются: 1) входящий поток – объекты, поступающие в систему через некоторые промежутки времени, 2) очередь, в которой данные объекты дожидаются обслуживания, 3) система пунктов обслуживания, 4) выходящий поток – объекты покидают систему.

Независимо от конкретной природы и характера объектов, поступающих в систему обслуживания, их называют требованиями (или заявками).
Входящий поток
событий мы будем считать простейшим (пуассоновским), т.е. вероятность
поступления того или иного числа требований в течение интервала времени ![]() зависит только от протяженности
этого интервала и не зависит от его расположения на оси времени (стационарность),
требования поступают по одному (ординарность), и не зависит от того каким
был предыдущий интервал времени между событиями (отсутствие последействия).
Простейший поток событий характеризуется распределением Пуассона:
зависит только от протяженности
этого интервала и не зависит от его расположения на оси времени (стационарность),
требования поступают по одному (ординарность), и не зависит от того каким
был предыдущий интервал времени между событиями (отсутствие последействия).
Простейший поток событий характеризуется распределением Пуассона:
![]() ,
,
где ![]() -
вероятность поступления
-
вероятность поступления ![]() требований за
время
требований за
время ![]() в простейшем потоке интенсивностью
в простейшем потоке интенсивностью ![]() .
.
При
исследовании систем массового обслуживания наибольший интерес представляет
предельный стационарный режим, который наступает при ![]() . В этом режиме система также меняет
свои состояния случайным образом, но вероятности состояний
. В этом режиме система также меняет
свои состояния случайным образом, но вероятности состояний ![]() (
(![]() )
уже не зависят от времени. Каждая из них, являясь постоянной величиной,
характеризует относительное время пребывания системы в данном состоянии.
)
уже не зависят от времени. Каждая из них, являясь постоянной величиной,
характеризует относительное время пребывания системы в данном состоянии.
Стационарный режим описывается системой алгебраических уравнений, которая получается из системы дифференциальных уравнений Колмогорова путем приравнивания нулю всех производных по времени.
Приведем еще несколько важных характеристик системы:
1) относительная пропускная способность q, показывающая вероятность того, что поступившее в систему требование будет обслужено;
2) среднее число занятых каналов kср, представляющее собой математическое ожидание числа занятых каналов;
3) средняя
длина очереди ![]() , определяемая как
математическое ожидание числа находящихся в очереди требований.
, определяемая как
математическое ожидание числа находящихся в очереди требований.
Запишем формулы нахождения основных характеристик для частных случаев систем массового обслуживания.
1)Чистая система с ожиданием (уходов из очереди нет).
Предельные вероятности состояния системы:
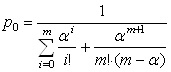 ,
, ![]() ,
,
![]() ,
,
где m
– число каналов обслуживания, ![]() - приведенная
плотность входящего потока требований;
- приведенная
плотность входящего потока требований; ![]() ,
, ![]() – интенсивность входящего потока и
обслуживания требований одним каналом соответственно, r
– длина очереди.
– интенсивность входящего потока и
обслуживания требований одним каналом соответственно, r
– длина очереди.
Поясним смысл a. Она показывает, сколько заявок
поступает в систему за время обслуживания одной заявки ![]() ,
или сколько необходимо пунктов обслуживания, чтобы справиться с потоком заявок.
,
или сколько необходимо пунктов обслуживания, чтобы справиться с потоком заявок.
Выражение для ![]() справедливо, если
справедливо, если ![]() . Это условие стационарности
процесса.
. Это условие стационарности
процесса.
Средняя
длина очереди ![]() определяется как:
определяется как: ![]() .
.
2) Система с отказами (очередь отсутствует, r=0).
 ,
, ![]() ,
,
Вероятность
отказа: ![]() .
.
Относительную
пропускную способность находим как: ![]() .
.
Среднее число
занятых каналов: ![]() .
.
Задача №1.
Среднее число вызовов, поступающих на коммутатор за минуту, равно 3. Найти вероятность того, что за 2 минуты поступит: а) 4 вызова; б) менее четырех вызовов; в) более четырех вызовов. Входящий поток требований считать простейшим.
Решение:
Из условий
задачи следует, что ![]() . Найдем вероятность, что
за 2 минуты в систему обслуживания (коммутатор) поступит 4 вызова:
. Найдем вероятность, что
за 2 минуты в систему обслуживания (коммутатор) поступит 4 вызова:
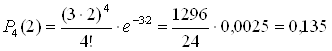 .
.
Найдем вероятность того, что за 2 минуты на коммутатор поступит менее 4-х вызовов, т.е. 0,1,2 или 3:
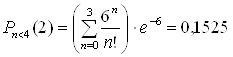

Теперь найдем вероятность того, что за 2 минуты на коммутатор поступит более 4-х вызовов (т.е. 5,6,7,…):
![]()
Задача №2.
На автозаправочную станцию поступает пуассоновский поток с
интенсивностью ![]() (автомашин в минуту).
Колонка обслуживает машину в среднем за 1,25 мин (
(автомашин в минуту).
Колонка обслуживает машину в среднем за 1,25 мин (![]() ).
Определить: 1) условие при котором система имеет стационарный режим; 2) среднее
число машин в очереди при трех работающих колонках (
).
Определить: 1) условие при котором система имеет стационарный режим; 2) среднее
число машин в очереди при трех работающих колонках (![]() )
и вероятность
)
и вероятность ![]() того, что длина очереди не
превышает количество колонок; 3) необходимое количество колонок, при котором
вероятность того, длина очереди превышает число колонок, меньше или равна 0,01.
Считать, что это чистая система с ожиданием.
того, что длина очереди не
превышает количество колонок; 3) необходимое количество колонок, при котором
вероятность того, длина очереди превышает число колонок, меньше или равна 0,01.
Считать, что это чистая система с ожиданием.
Решение:
1) Данная
система массового обслуживания представляет собой чистую систему с ожиданием.
Таким образом, процесс будет стационарным, если ![]() .
Находим:
.
Находим: ![]() .
.
Т.о. условием
стационарности является неравенство: ![]() .
.
2) Найдем значение вероятности, когда все каналы свободны:
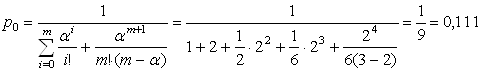 .
.
Среднее число машин в очереди при трех работающих колонках будет:
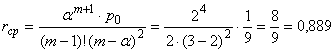 .
.
Вероятность того, длина очереди не превышает числа колонок (m=3), может быть найдена:
 .
.
Найдем неизвестные вероятности:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Получаем: ![]() .
.
3) Вероятность того, длина очереди превышает число колонок для m=3 равна:
![]() , что сильно превышает заданное в
условии значение.
, что сильно превышает заданное в
условии значение.
Рассмотрим
случай для ![]() . Находим вероятности:
. Находим вероятности:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
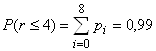 .
.
Отсюда получаем, что вероятность нахождения в очереди более 4-х машин равна:
![]() .
.
Т.е. для удовлетворения данного условия достаточно 4-х колонок.
Задача №3.
Телефонный
коммутатор обеспечивает не более 5 разговоров одновременно. Средняя длительность
разговора 2 мин, а вызовы поступают в среднем через 1 мин. Рассматривая коммутатор
как систему с отказами, определить относительную пропускную способность ![]() , среднее число занятых каналов
, среднее число занятых каналов ![]() и среднее время пребывания вызова на
коммутаторе
и среднее время пребывания вызова на
коммутаторе ![]() .
.
Решение:
Запишем параметры системы обслуживания:
![]() мин-1,
мин-1, ![]() мин-1,
мин-1, ![]() ,
, ![]() .
.
Теперь мы можем найти:
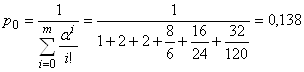 ,
,
![]() ,
,
![]() .
.
Среднее время пребывания вызова на коммутаторе можно найти как:
![]() ,
,
где ![]() .
.
Отсюда получаем:
![]() .
.
Задача №4.
Двое рабочих обслуживают группу из шести станков. Остановка каждого работающего станка происходит в среднем каждые полчаса. Процесс наладки занимает в среднем 10 мин. Определить среднюю занятость рабочих, среднее количество неисправных станков и среднее число станков, обслуживаемых в единицу времени (или абсолютную пропускную способность).
Решение:
Возможные состояния системы обслуживания
следующие: ![]() - все станки работают, рабочие не
заняты;
- все станки работают, рабочие не
заняты; ![]() - один станок остановился и один
рабочий занят; s2 — два
станка остановились, двое рабочих заняты;
- один станок остановился и один
рабочий занят; s2 — два
станка остановились, двое рабочих заняты;![]() -
-
![]() станков остановились, два из них
настраивают,
станков остановились, два из них
настраивают, ![]() ждут очереди (i = 3,4,
5, 6). Таким образом, система может быть представлена следующим графом
ждут очереди (i = 3,4,
5, 6). Таким образом, система может быть представлена следующим графом
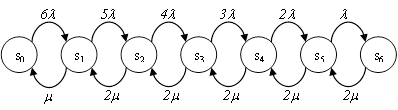
Здесь ![]() –
интенсивность потока требований (2 станка в час);
–
интенсивность потока требований (2 станка в час); ![]() –
интенсивность обслуживания (6 станков в час).
–
интенсивность обслуживания (6 станков в час).
Теперь мы можем составить уравнения для стационарного режима:

Отсюда находим вероятности состояний:
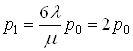 ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Чтобы найти ![]() используем
условие нормировки:
используем
условие нормировки:
![]() ;
;
откуда следует, что:
![]() .
.
Средняя число занятость рабочих (или среднее число занятых каналов kср) определяется математическим ожиданием числа занятых рабочих, с использованием уже известного распределения числа неисправных станков:
![]() ,
,
![]() .
.
Среднее число неисправных станков равно математическому ожиданию распределения станков, связанных с процессом обслуживания (налаживаются или ожидают очереди):
![]() ,
,
![]() .
.
При интенсивности обслуживания ![]() среднее число станков,
обслуживаемых в единицу времени, т. е. абсолютная пропускная способность:
среднее число станков,
обслуживаемых в единицу времени, т. е. абсолютная пропускная способность:
![]() ст/час.
ст/час.