1. ЭНТРОПИЯ КАК МЕРА СТЕПЕНИ НЕОПРЕДЕЛЕННОСТИ
Сообщением является последовательность дискретных элементов (знаков, символов) или непрерывная функция. Следует отметить, что все реальные сообщения в виде непрерывных функций могут быть сведены к последовательностям дискретных элементов.
Устройство, явление или причину, порождающие сообщения, удобно толковать как источники информации, обладающие определенным алфавитом, который должен быть известен до начала проведения измерений или расчетов количества информации. Источники информации могут быть дискретными и непрерывными, в соответствии с видом порождаемых сообщений. Мы в дальнейшем будем в основном рассматривать дискретные источники.
Дискретный источник обладает конечным алфавитом из М элементов, обозначаемых х1, х2, … , хi, … , хМ, каждый из которых характеризуется вероятностью Р(х1), Р(х2), … , Р(хi), …, Р(хМ) появления в сообщении. То есть мы опять имеем дело со случайными событиями.
Совокупность элементов и их вероятностей удобно задавать в виде матрицы:
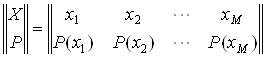
В большинстве реальных случаев появление элемента хi в сообщении зависит от того, какой элемент хj был предшествующим. Взаимосвязь элементов в сообщении характеризуется матрицей условных вероятностей:

При отсутствии взаимосвязи элементов:
![]()
Неопределенность
выбора элементов ![]() при создании сообщения
удобно характеризовать энтропией источника
при создании сообщения
удобно характеризовать энтропией источника ![]() .
При независимых элементах:
.
При независимых элементах:
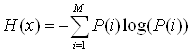
При зависимых
элементах с условными вероятностями сначала определяется частная условная
энтропия, вычисленная по предыдущей формуле, но в предположении зафиксированного
предыдущего элемента ![]() :
:

Величина ![]() случайная, так как случайным
является предшествующий элемент
случайная, так как случайным
является предшествующий элемент ![]() . Поэтому для получения
полной энтропии источника необходимо произвести усреднение по вероятностям
появления предшествующих элементов:
. Поэтому для получения
полной энтропии источника необходимо произвести усреднение по вероятностям
появления предшествующих элементов:
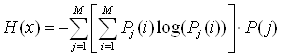
Это формула средней условной энтропии или просто энтропии источника, которая учитывает взаимозависимость элементов в сообщении.
Задача №1
Пусть из многолетних наблюдений за погодой известно, что для определенного пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того, что в указанный день дождя не будет, равна 0,6. Пусть далее для этого же пункта вероятность того, что 15 ноября будет идти дождь равна 0,65, вероятность, что будет идти снег – 0,15 и вероятность того, что 15 ноября вовсе не будет осадков равна 0,2. В какой из двух перечисленных дней погоду в рассматриваемом пункте следует считать более неопределенной: 1) если из всех характеристик погоды интересоваться вопросом о характере осадков; 2) если интересоваться лишь вопросом о наличии осадков.
Решение:
Согласно тому, как понимается здесь слово «погода» имела место 15 июля и 15 ноября, характеризуется следующими таблицами вероятностей:
опыт a1
|
исходы опыта |
дождь |
отсутствие осадков |
|
вероятность |
0,4 |
0,6 |
опыт a2
|
исходы опыта |
дождь |
снег |
отсутствие осадков |
|
вероятность |
0,65 |
0,15 |
0,2 |
1) Поэтому энтропии наших двух опытов равны
![]()
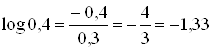

![]()


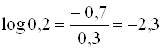
Поэтому погоду 15 ноября в рассматриваемом пункте следует считать более неопределенной, чем 15 июня.
2) Если интересоваться только тем, будут в рассматриваемый день осадки или нет, то исходы «снег» и «дождь» опыта a2 следует объединить:
![]()
![]()
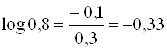
Тогда погоду 15 ноября в рассматриваемом пункте следует считать менее неопределенной, чем 15 июня.
Задача №2
На выходе
двоичного источника информации элементы «0» и «1» появляются с вероятностями
соответственно Р и (1-Р). При каком значении Р энтропия источника максимальна?
Построить график зависимости ![]() для двоичного
источника.
для двоичного
источника.
Решение:
1) Строим функциональную зависимость величины энтропии от вероятности Р:
![]() .
.
Найдем значение Р, при котором данная функция принимает максимальное значение. Для этого ищем экстремум функции:
![]()
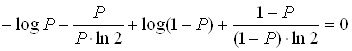
![]()
![]()
![]()
![]()
![]() , т.о.
, т.о. ![]()
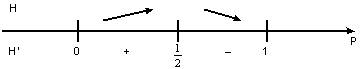
Это подтверждает свойство энтропии, что она максимальна при равновероятных элементах, т.е. Р=1/2.
2) Зная
функциональную зависимость ![]() получаем
следующий график:
получаем
следующий график:


![]()
![]()

Задача №3
Имеются два дискретных троичных источника с независимыми элементами. На выходе каждого источника появляются сообщения одинаковой длины – по 15 элементов. Количество различных элементов в сообщении каждого источника постоянно. Сообщения каждого источника отличаются только порядком следования элементов, а состав сообщений постоянный. Зафиксированы два типичных сообщения: 021202120212021 – первого источника и 012101201101201 – второго. Для какого источника неопределенность появления элементов выше?
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
Для первого источника:
![]()
Для второго источника:
![]()
Напомним, что
средняя условная энтропия опыта ![]() при
условии выполнения опыта
при
условии выполнения опыта ![]() находится по
формуле (см. лекции):
находится по
формуле (см. лекции):
![]()
Задача №4
Пусть опыты ![]() и
и ![]() состоят
в последовательном извлечении двух шаров из урны, содержащей m
черных и (n-m) белых шаров (
состоят
в последовательном извлечении двух шаров из урны, содержащей m
черных и (n-m) белых шаров (![]() - извлечение первого шара и
- извлечение первого шара и ![]() - извлечение второго шара). Чему
равна энтропия
- извлечение второго шара). Чему
равна энтропия ![]() ,
, ![]() и
условная энтропия
и
условная энтропия ![]() ?
?
Решение:
![]() .
.
Обозначим:
А1 – первый раз извлекли черный шар, А2 – первый раз извлекли белый шар;
В1 – второй раз извлекли черный шар, В2 – второй раз извлекли белый шар;
Если нам известен исход опыта ![]() , то:
, то:
![]() ,
,![]()

![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Теперь, по формуле полной вероятности
 , i={1,2}
, i={1,2}
можно определить безусловные
вероятности опыта ![]() :
:
![]() ,
,
![]() .
.
Таким образом, безусловная
энтропия опыта ![]() равна безусловной энтропии
опыта
равна безусловной энтропии
опыта ![]() .
.
Найдем частные условные
энтропии опыта ![]() , что:
, что:
![]() ,
,
![]() .
.
![]()
И, наконец, находим:
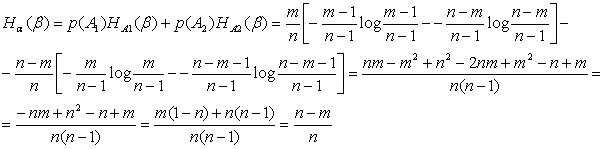
Задача №5
Ракеты двух пусковых установок используются для поражения двух целей. Ракета, пущенная с первой установки, поражает цель номер один с вероятностью 0,5, цель номер два – с вероятностью 0,3, и дает промах с вероятностью 0,2. Ракета второй установки поражает первую цель вероятностью 0,3, а вторую – с вероятностью 0,5 и вероятность промаха 0,2. Вероятность выбора первой установки 0,4. Чему равна неопределенность выбора установки: 1) если известно, что поражена вторая цель; 2) если произошел промах? Какова неопределенность исхода, если пущена любая ракета?
Решение:
Полагаем, что варианты поражения целей соответствуют случайному опыту В, а выбор ракетной установки – опыту А. Вероятности поражения целей ракетами различных установок представляют собой условные вероятности:
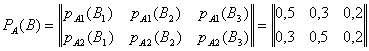
![]()
Неопределенность выбора установки при условии, что поражена вторая цель представляет собой энтропию:
![]()
Неопределенность выбора установки в случае промаха есть энтропия:
![]()
Поэтому нам
необходимо найти условные вероятности ![]() и
и ![]() . Для этого определяем элементы матрицы
. Для этого определяем элементы матрицы
![]() по формуле полной вероятности:
по формуле полной вероятности:
![]()
![]()
Теперь мы можем найти условные вероятности (см. тему «условные вероятности»):
![]()
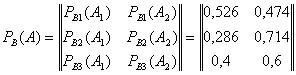
В результате находим:
![]()
Неопределенность ситуации, если запущена любая ракета, характеризуется средней условной энтропией:
![]()
Задача №6
Найти энтропию источника, описываемого графом вероятностей перехода.
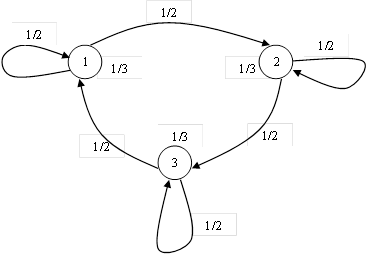
Решение:
Составляем матрицы вероятностей состояний и условных вероятностей:
![]()


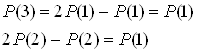
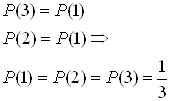
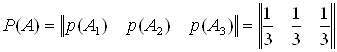
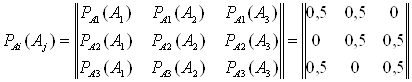
Теперь находим среднюю условную энтропию:
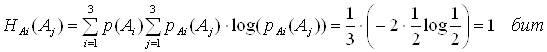
Задача №7
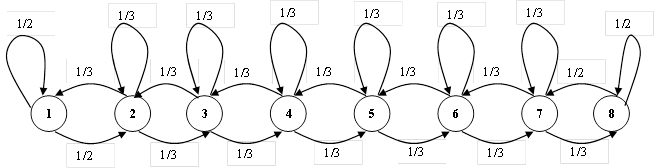
Определить максимальную энтропию телевизионного изображения, содержащего 500 строк по 650 элементов в строке, при условии, что яркость каждого элемента передается восьмью квантованными уровнями, если: а) уровни не коррелированны; б) статистическая связь между различными градациями яркости задана графом
Решение:
а) Максимальная энтропия одного элемента изображения, при условии, что уровни не коррелированны, составляет (энтропия максимальна в случае, если уровни являются равновероятными):
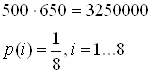
![]() .
.
Так как, у
нас элементов 500х650, то возможное количество состояний изображения ![]() , а максимальная энтропия
телевизионного изображения равна:
, а максимальная энтропия
телевизионного изображения равна:
![]() .
.
б) Найдем максимальную среднюю условную энтропию одного элемента. Для этого, исходя из приведенного графа, составим матрицу условных переходных вероятностей:

Уровни считаем равновероятными, так как ищем максимальную энтропию, значит:
![]()
Теперь находим максимальную среднюю условную энтропию одного элемента изображения:

Отсюда максимальная энтропия телевизионного изображения равна:
![]()
Задача №8
Дана матрица вероятностей совместных событий:
 .
.
Определить
энтропии ![]() ,
,![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
Решение:

1) ![]()

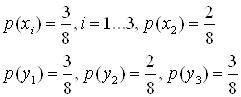

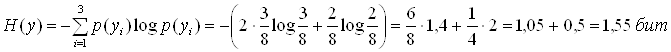
![]() ,
,![]() ,
,
![]() .
.
2) ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
3) ![]() ,
, ![]() ,
,
![]()

![]()
,
![]() .
.
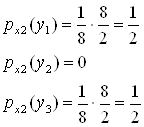
4) 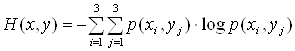 или
или ![]()


![]()
![]()
![]()
![]()

Задача №9
Информация передается при помощи частотно-модулированных сигналов, рабочая частота F которых изменяется с равной вероятностью в пределах от F1=10МГц до F2=50МГц. Определить энтропию значения частоты, если точность измерения частоты DF=2кГц.
Решение:
Так как
точность измерений составляет DF=2кГц, то мы имеем дело с ![]() числом
равновероятных исходов.
числом
равновероятных исходов.
![]()
Поэтому энтропия частоты будет определяться:
![]()
Задача №10
Дан сигнал с
распределением ![]() , который затем был
квантован с точностью 1В.
, который затем был
квантован с точностью 1В.
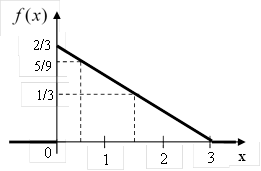
Известно, что появление уровней сигнала имеет по-парную зависимость, которая представлена матрицей условных вероятностей:

Найти среднюю
условную энтропию сигнала ![]() .
.
Решение:
Вероятности
уровней находим из графика ![]() . В нашем случае:
. В нашем случае:
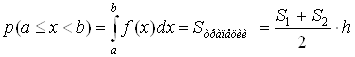 ,
,
где S1 , S2 – основания трапеции, h – высота трапеции.
Так как
говорится о точности 1В, то вероятность нахождения в 0-ом состоянии будет равно
площади фигуры ограниченной функцией f(x), осью Ox и
прямыми х=0 и х=1, то есть ![]() .
Так же находим:
.
Так же находим:
![]() ,
,
![]() .
.
Теперь мы
можем найти энтропию данного сигнала![]() :
:
![]()
![]()
![]()
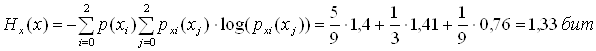
Напомним некоторые свойства энтропии источников информации.
1) Условная энтропия источника всегда меньше безусловной:
![]() .
.
2) Если составной источник состоит из источников информации X иY, то для случая независимых источников:
![]() ,
,
а для случая зависимых друг от друга источников:
![]() или
или ![]() .
.
Задача №11
Элементы
алфавитов X и Y статистически
связаны. Известно, что ![]() ,
, ![]() . В каких пределах меняется условная
энтропия
. В каких пределах меняется условная
энтропия ![]() при изменении
при изменении ![]() в максимально возможных пределах?
в максимально возможных пределах?
Решение:
Т.к.: ![]() и
и ![]() ,
то можем записать
,
то можем записать
![]() .
.
Условная
энтропия может изменяться : ![]() , поэтому
значения какие будет принимать
, поэтому
значения какие будет принимать ![]() при изменении
при изменении ![]() можно определить:
можно определить:
![]()
При
минимальном значении ![]() :
: ![]() .
.
При
максимальном значении ![]() :
: ![]() .
.
Запишем, чему равна приведенная энтропия непрерывной случайной величины, сигнала или события, подчиняющихся нормальному закону распределения:
![]()
Задача №12
В результате
полной дезорганизации управления самолеты летят произвольными курсами.
Управление восстановлено, и все самолеты взяли общий курс со
среднеквадратической ошибкой отклонения от курса ![]() .
Найти изменение энтропии, считая, что в первом случае имело место равномерное
распределение вероятностей углов, а во втором случае – нормальное.
.
Найти изменение энтропии, считая, что в первом случае имело место равномерное
распределение вероятностей углов, а во втором случае – нормальное.
Решение:
Рассмотрим каждый самолет, как случайную величину. Так, как в первом случае имеет место равномерное распределение вероятностей углов, а у нас углы изменяются от 0 до 360о, то функция распределения вероятности для одного самолета равна f(x)=1/360. Для равновероятных случайных величин:
Для первого случая:
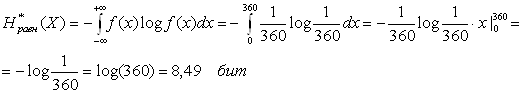 .
.
Для второго случая считаем по приведенной выше формуле:
![]() .
.
Таким образом изменение энтропии составит:
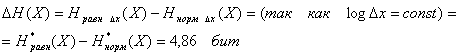
Добавочные задачи
Задача №13.
Имеются два дискретных источника информации, заданных следующими таблицами вероятностей:
|
Х |
х1 |
х2 |
|
вероятность |
р1 |
р2 |
и
|
Y |
y1 |
y2 |
y3 |
|
вероятность |
q1 |
q2 |
q3 |
Определить, какой источник обладает большей неопределенностью в случае, если: а) p1 = p2, q1 = q2 = q3 ; б) p1 = q1 , p2 = q2 + q3 .
Решение:
1) В случае равновероятных элементов большей неопределенностью обладает троичный источник. При этом неопределенность может быть подсчитана, как logM, где М – число равновероятных состояний.
2) Запишем:
![]()
![]()


Отсюда
следует, что ![]() .
.
Задача №14.
Определить среднюю неопределенность появления одного символа сообщения 01001000101001, при условии, что вероятность появления элементов на выходе источника информации с течением времени не изменяется, а приведенная последовательность символов – типичная.
Решение:
![]()
Задача №15.
Измерительное устройство регистрирует временные интервалы, распределенные случайным образом в пределах от 100 до 500мс. Как изменится энтропия случайной величины при изменении точности измерения с 1мс до 1мкс?
Решение:
При точности измерения 1мс случайная величина принимает (500-100)/1=400 равновероятных значений, а значит ее энтропия:
![]()
А при точности измерения 1мкс случайная величина принимает (500-100)/0.001=400000 равновероятных значений, а значит ее энтропия:
![]() .
.
Значит, энтропия случайной величины увеличится примерно на 10 бит.
Задача №16.
Опыт Х –
случайный выбор целого числа от 1 до 1050. Опыт Y –
определение величин остатков от деления этого числа на 35. Определить энтропии
![]() ,
,![]() ,
,![]() .
.
Решение:
Чтобы найти
энтропии ![]() ,
, ![]() строим
вероятностные схемы для X и Y.
строим
вероятностные схемы для X и Y.
т.к. Х может принимать равновероятные значения от 1 до 1050, то получаем:
![]() ,
,
т.к. при делении на 35, остаток от деления может принимать 35 равновероятных значений от 0 до 34, а значит
![]()
Находим:
![]() ,
, ![]()
Для
определения ![]() построим матрицу
построим матрицу ![]() . При построении данной матрицы будем
исходить из следующих соображений, если мы имеем остаток от деления на 35
. При построении данной матрицы будем
исходить из следующих соображений, если мы имеем остаток от деления на 35 ![]() , то этому должны отвечать числа
, то этому должны отвечать числа
![]() ,
,![]() ,…,
,…,![]() , которые отстоят друг от друга на 35
и количество этих чисел равно 1050/35=30. Так как числа равновероятные, то
вероятности их появления при условии, что остаток от деления равен 0,
составляет 1/30. Тоже самое относится к значениям Х при условии других остатков
от деления. Т.о. получаем:
, которые отстоят друг от друга на 35
и количество этих чисел равно 1050/35=30. Так как числа равновероятные, то
вероятности их появления при условии, что остаток от деления равен 0,
составляет 1/30. Тоже самое относится к значениям Х при условии других остатков
от деления. Т.о. получаем:

Находим:
![]()
2. ИНФОРМАЦИЯ
Информация в сложном опыте:
![]() где
где ![]() -
опыт, предшествующий опыту
-
опыт, предшествующий опыту ![]() , снижающий
степень его неопределенности.
, снижающий
степень его неопределенности.
Важной характеристикой источника сообщений является его избыточность, под которой понимается отношение:
 ,
,
где ![]() - энтропия рассматриваемого
источника,
- энтропия рассматриваемого
источника, ![]() - максимально возможное значение его
энтропии, которое может быть достигнуто подбором распределения и ликвидацией
взаимозависимости элементов алфавита. Так для дискретного источника с М
элементами:
- максимально возможное значение его
энтропии, которое может быть достигнуто подбором распределения и ликвидацией
взаимозависимости элементов алфавита. Так для дискретного источника с М
элементами:
![]() .
.
Если элементы
независимы, ![]() определится по формуле:
определится по формуле:
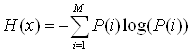
При зависимых попарно элементах энтропия находится по уже известной формуле:
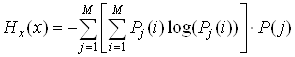
Задача №1.
Пусть опыт ![]() состоит в предварительном извлечении
из урны, содержащей 5 черных и 10 белых шаров, без возвращения обратно 1 шара,
а опыт
состоит в предварительном извлечении
из урны, содержащей 5 черных и 10 белых шаров, без возвращения обратно 1 шара,
а опыт ![]() состоит в извлечении одного шара из той
же урны. Чему равна безусловная энтропия опыта
состоит в извлечении одного шара из той
же урны. Чему равна безусловная энтропия опыта ![]() и
информация об этом опыте, содержащаяся в опыте
и
информация об этом опыте, содержащаяся в опыте ![]() ?
?
Решение:
Опыт ![]() имеет исходы – А1
и А2 (извлекли черный или белый шар первый раз соответственно), а
опыт
имеет исходы – А1
и А2 (извлекли черный или белый шар первый раз соответственно), а
опыт ![]() - В1 и В2
(извлекли черный или белый шар во второй раз). Чтобы найти безусловную энтропию
опыта
- В1 и В2
(извлекли черный или белый шар во второй раз). Чтобы найти безусловную энтропию
опыта ![]() надо найти безусловные вероятности
наступления событий В1 и В2.
надо найти безусловные вероятности
наступления событий В1 и В2.
![]() ,
,
![]() .
.
Т.о. безусловная
энтропия опыта ![]() равна (если мы ничего не
знаем об опыте
равна (если мы ничего не
знаем об опыте ![]() ):
):
![]()
Теперь находим:

![]()
![]()
![]()
![]()
Задача №2.
Пусть опыт ![]() состоит в определении положения
некоторой точки М, относительно которой заранее известно только то, что она
расположена на отрезке АВ длины L, а опыт
состоит в определении положения
некоторой точки М, относительно которой заранее известно только то, что она
расположена на отрезке АВ длины L, а опыт ![]() - в измерении длины отрезка АМ с
помощью некоторого измерительного прибора, дающего нам значение длины с
точностью до определенной "ошибки измерения"
- в измерении длины отрезка АМ с
помощью некоторого измерительного прибора, дающего нам значение длины с
точностью до определенной "ошибки измерения" ![]() .
Пусть перед нами стоит задача определить положение точки с точностью до
величины
.
Пусть перед нами стоит задача определить положение точки с точностью до
величины ![]() . Чему равна информация
. Чему равна информация ![]() , содержащаяся в результате
измерения, относительно истинного положения точки?
, содержащаяся в результате
измерения, относительно истинного положения точки?
Решение:
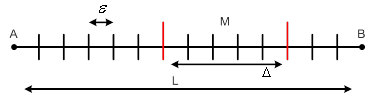
Так как,
нам заранее известно, что точка М располагается где-то на отрезке АВ, то мы
можем считать, что опыт ![]() , состоящий в
определении ее положения с точностью до
, состоящий в
определении ее положения с точностью до ![]() ,
имеет
,
имеет ![]() равновероятных исходов. Так что его
энтропия равна:
равновероятных исходов. Так что его
энтропия равна:
![]() .
.
После того,
как мы произвели опыт ![]() , т.е. измерили длину АМ с
помощью измерительного прибора, мы выяснили, что на самом деле точка М
помещается внутри меньшего интервала
, т.е. измерили длину АМ с
помощью измерительного прибора, мы выяснили, что на самом деле точка М
помещается внутри меньшего интервала ![]() , поэтому при
известном исходе
, поэтому при
известном исходе ![]() опыт
опыт ![]() будет иметь уже
будет иметь уже ![]() равновероятных исходов. Отсюда
находим:
равновероятных исходов. Отсюда
находим:
![]() .
.
Следовательно:
![]() .
.
Видно, что при неограниченном увеличении точности прибора искомая информация неограниченно возрастает. Правда возрастание это будет медленным. Так при увеличении точности в n раз мы получаем дополнительно лишь log(n) единиц информации (например, при увеличении точности в 2 раза мы выгадываем 1 бит информации, а в 1000 раз – менее 10 бит).
Задача №3.
Определить среднюю взаимную информацию между двумя буквами алфавита, если известно, что средняя безусловная энтропия, приходящаяся на одну букву алфавита, равна 5 бит, а энтропия на пару букв равняется 8,3 бита.
Решение:
Информация, которую несет в себе одна буква о другой определяется:
![]()
![]() , а
, а ![]()
Известно,
что: ![]() . Значит:
. Значит:
![]()
Теперь
находим: ![]() .
.
Задача №4.
Какое количество информации получает в среднем человек, определяющий день рождения своего собеседника, когда последний сообщает ему месяц, в котором он родился?
Решение:
Обозначим
опыт, заключающийся в определении дня рождения, как ![]() ,
а опыт заключающийся в угадывании месяца –
,
а опыт заключающийся в угадывании месяца – ![]() .
Тогда нам нужно найти:
.
Тогда нам нужно найти: ![]() .
.
Первый способ.
Энтропия опыта ![]() сначала равна:
сначала равна:
![]() (т.к. опыт имеет 365 равновероятных
исходов)
(т.к. опыт имеет 365 равновероятных
исходов)
Когда
проводим опыт ![]() , то энтропия опыта
, то энтропия опыта ![]() будет равна:
будет равна:
![]() (т.к. число исходов опыта снижается
до 30).
(т.к. число исходов опыта снижается
до 30).
Тогда: ![]()
Второй способ.
С другой стороны: ![]() .
.
Неопределенность,
того в какой месяц родился человек: ![]() бита
бита
Если нам
сообщают о дне рождения человека, то неопределенность месяца в котором он
родился будет равна нулю: ![]() , т.е.
, т.е. ![]() бита.
бита.
Задача №5.
Определить количество информации, которое содержится в сообщении о том, что сумма выпавших очков на двух игральных костях равна семи.
Решение:
Опыт ![]() - определение числа очков выпавших
на двух костях,
- определение числа очков выпавших
на двух костях, ![]() - сообщение о том, что
сумма выпавших очков равна 7.
- сообщение о том, что
сумма выпавших очков равна 7.
Найдем:
![]() .
.
![]() ,
, ![]()
Т.о.: ![]()
Задача №6.
Радиостанция может работать на волне ![]() (событие А1) или на волне
(событие А1) или на волне ![]() (событие А2); в импульсном
(событие В1) или непрерывном (событие В2) режимах.
Вероятности совместных событий имеют следующие значения:
(событие А2); в импульсном
(событие В1) или непрерывном (событие В2) режимах.
Вероятности совместных событий имеют следующие значения: ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
Вычислить количество информации, полученное относительно режима работы станции,
если станет известной длина волны станции.
.
Вычислить количество информации, полученное относительно режима работы станции,
если станет известной длина волны станции.
Решение:
Нам надо найти:
![]()
Необходимо найти:
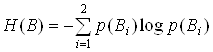 и
и 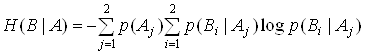
Найдем:
 , значит
, значит ![]() ,
,
![]()
![]()
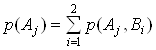 , значит
, значит ![]() ,
, ![]()
![]()
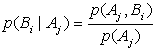 , значит
, значит ![]() ,
,![]() ,
,
![]() ,
, ![]()
В результате получаем:
![]() ,
, ![]()
![]()
Задача №7
Избыточность ряда европейских языков лежит в пределах 50-65%. Определить энтропию их алфавитов, если считать, что число букв в алфавите европейских языков равняется 26.
Решение:
Число букв в алфавите европейских языков равняется 26, значит максимально
возможное значение его энтропии: 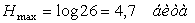 .
.
Т.о. исходя из того, что: ![]() ,
,
можно найти энтропию алфавита: ![]() .
.
3. ПЕРЕДАЧА ИНФОРМАЦИИ ПО КАНАЛАМ СВЯЗИ.
ПЕРЕДАЧА ДИСКРЕТНЫХ ЭЛЕМЕНТОВ
Канал
связи представляет собой совокупность технических средств для передачи
сообщений из одной точки пространства в другую. Передача чаще всего
осуществляется в условиях помех, в результате воздействия которых
отправленный элемент ![]() может быть опознан получателем,
как
может быть опознан получателем,
как ![]() , причем
, причем ![]() .
Это событие называется ошибкой.
.
Это событие называется ошибкой.
Передачу элементов сообщения можно рассматривать
как составной эксперимент, состоящий в отправлении элементов сообщения ![]() и получении элементов
и получении элементов ![]() . Свойства канала при этом полностью
описываются матрицей переходных вероятностей
. Свойства канала при этом полностью
описываются матрицей переходных вероятностей ![]() или
или
![]() , где
, где ![]() -
вероятность отправления элемента
-
вероятность отправления элемента ![]() , если
зафиксирован полученный элемент
, если
зафиксирован полученный элемент ![]() , а
, а ![]() - вероятность получения элемента
- вероятность получения элемента ![]() , если зафиксирован (отправляется) элемент
, если зафиксирован (отправляется) элемент
![]() .
.
Если помех нет, то все диагональные элементы этих матриц равны единице, а остальные нулю. При очень больших помехах все элементы матриц могут быть приблизительно одинаковыми.
При наличии
помех отправление элемента ![]() не снимает
полностью неопределенность относительно полученного элемента
не снимает
полностью неопределенность относительно полученного элемента ![]() . Таким образом, ситуация передачи
сообщения описывается четырьмя мерами неопределенности:
. Таким образом, ситуация передачи
сообщения описывается четырьмя мерами неопределенности:
1)
неопределенность отправляемых элементов ![]() :
:
![]() ,
,
(здесь предположена
независимость элементов ![]() )
)
2)
неопределенность полученных элементов ![]() :
:
![]() ,
,
3)
неопределенность получения элементов ![]() при
известных отправляемых элементах
при
известных отправляемых элементах ![]() :
:
![]() ,
,
Это средняя
условная энтропия получаемых элементов. Здесь в формуле ![]() - частная условная энтропия
принятых элементов.
- частная условная энтропия
принятых элементов.
4)
неопределенность отправления элементов ![]() при
известных получаемых элементах
при
известных получаемых элементах![]() :
:
![]() .
.
Это средняя
условная энтропия отправляемых элементов. Здесь в формуле ![]() - частная условная энтропия
отправляемых элементов.
- частная условная энтропия
отправляемых элементов.
Количество переданной информации по каналу связи можно оценить по уже известной формуле:
![]() .
.
Задача №1.
Определить
среднее количество передаваемой информации ![]() ,
если матрица системы передачи информации
,
если матрица системы передачи информации ![]() имеет
вид
имеет
вид
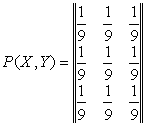
Здесь X, Y – передаваемый и принимаемый сигнал соответственно.
Решение:
Количество переданной информации по каналу связи:
![]()
Необходимо найти:
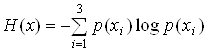 и
и 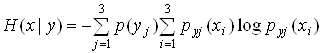
Найдем:
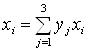
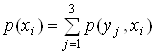 , значит
, значит ![]() .
.
 , значит
, значит ![]() .
.
 , значит
, значит ![]()
В результате получаем:
![]()
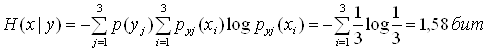
![]()
Т.е. сигналы X и Y взаимно независимые и передачи информации нет (из-за сильных помех).
Задача №2.
Определить
среднее количество информации ![]() передаваемой в
системе, описываемой матрицей
передаваемой в
системе, описываемой матрицей
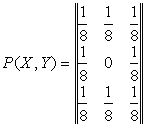 .
.
Здесь X, Y – передаваемый и принимаемый сигнал соответственно.
Решение:
Среднее количество информации в системе определяем как:
![]()
Необходимо найти:
![]() и
и 
Найдем:
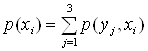 , значит
, значит ![]() ,
,
![]()
![]() , значит
, значит ![]() ,
,
![]()
![]() , значит
, значит ![]() ,
,
![]()
В результате получаем:
![]() ,
,


![]()
![]()
Основные параметры системы передачи
При рассмотрении взаимодействия источника информации и канала вводятся следующие важные понятия: производительность источника, пропускная способность канала и скорость передачи информации.
Под
производительностью источника понимается скорость создания информации, т.е. количество
информации, создаваемое источником в единицу времени (обычно в секунду). Для дискретного
источника, создающего ![]() элементов в секунду,
производительность:
элементов в секунду,
производительность:
![]() ,
,
где ![]() – энтропия, приходящаяся на один
элемент источника в среднем.
– энтропия, приходящаяся на один
элемент источника в среднем.
Под скоростью передачи информации по каналу понимается количество информации, передаваемое по каналу (или получаемое приемником) в единицу времени. Для дискретного источника скорость передачи информации
![]() ,
,
где ![]() – энтропия отправленных
последовательностей B составленных из элементов
– энтропия отправленных
последовательностей B составленных из элементов ![]() ,
, ![]() –
условная энтропия отправленных последовательностей с учетом полученных последовательностей
–
условная энтропия отправленных последовательностей с учетом полученных последовательностей
![]() элементов
элементов ![]() ,
,
![]() – длительность отправления
последовательности B.
– длительность отправления
последовательности B.
Если элементы
в последовательности на входе приемника появляются независимо со скоростью ![]() элементов в секунду, то
элементов в секунду, то
![]() ,
,
где ![]() и
и
![]() - неопределенность отправляемых
элементов и неопределенность отправляемых элементов X с
учетом полученных Y, соответственно.
- неопределенность отправляемых
элементов и неопределенность отправляемых элементов X с
учетом полученных Y, соответственно.
Под пропускной способностью канала понимается максимально возможная скорость передачи информации, которой можно достигнуть выбором кодирования:
![]() .
.
Если в канале
связи присутствуют помехи, то, используя помехоустойчивое кодирование,
максимизируют ![]() . Если помех нет, то
оптимальным кодированием добиваются максимальной скорости передачи
последовательностей элементов
. Если помех нет, то
оптимальным кодированием добиваются максимальной скорости передачи
последовательностей элементов ![]() .
.
Задача №3.
Лектор произносит в среднем около сорока шестибуквенных слов в минуту. Рассматривая его как источник дискретных сообщений, определить его производительность. Для простоты принять, что все буквы алфавита появляются равновероятно и статистически независимо друг от друга. Число букв считать равным 32.
Решение:
Средняя
энтропия одной буквы алфавита: ![]()
Энтропия
шестибуквенного слова: ![]()
В секунду
лектор произносит ![]() слов в секунду, значит его
производительность:
слов в секунду, значит его
производительность:
![]() .
.
Задача №4.
Определить
количество информации, передаваемое по двоичному симметричному каналу, и
скорость передачи информации, если скорость появления элементов на выходе
канала ![]() .
.
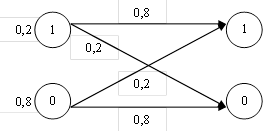

Решение:
Информация, передаваемая по каналу, определяется:
![]()
Нам известно: ![]()
![]() ,
,
![]() .
.
Поэтому можно найти:
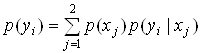 , находим:
, находим:
![]() ,
,
![]() .
.
Отсюда:
![]() .
.
![]()
![]()
![]()
Значит: ![]() ,
,
![]() .
.
Задача №5.
Двоичный источник с равновероятными независимыми элементами имеет производительность 1000 бит/с. При передаче по каналу в среднем один из переданных 100 символов искажается. Определить скорость передачи информации по данному каналу в предположении, что пропускная способность канала связи больше производительности источника.
Решение:
Известно,
что ![]() . Т.к. источник двоичный с
равновероятными элементами, то:
. Т.к. источник двоичный с
равновероятными элементами, то:
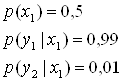
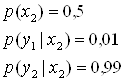
![]()
![]()
![]() .
.
Найдем скорость передачи информации:
![]()
Из условия задачи следует, что вероятность безошибочной передачи:
![]() ,
,
а передачи
с ошибкой: ![]() .
.
Т.к. передаваемые элементы равновероятные и линия симметричная, то:
![]()
![]()
Отсюда
находим: ![]() ,
,
![]()
В итоге получаем:
![]()
Пропускная способность радиоканала при передаче.
При передаче непрерывных сообщений в условиях белых гауссовских помех пропускная способность радиоканала:
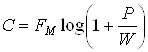 ,
,
где
![]() – полоса частот пропускания канала
(Гц),
– полоса частот пропускания канала
(Гц), ![]() и
и ![]() –
средние мощности сообщений и помехи соответственно. При этом сообщение должно
иметь нормальный закон распределения мгновенных значений.
–
средние мощности сообщений и помехи соответственно. При этом сообщение должно
иметь нормальный закон распределения мгновенных значений.
Задача №6.
Определить максимально возможную скорость передачи информации по радиоканалу, если рабочая полоса частот канала равна 100кГц, а отношение сигнал/шум равно 10.
Решение:
![]()
Задача №7.
Определить
полосу пропускания канала передачи телевизионного черно-белого изображения,
содержащего ![]() элементов. Изображение передается с
частотой 25 кадров/с. Каждый элемент имеет 8 равновероятных независимых
градаций яркости. Полезный сигнал распределен по нормальному закону, отношение
сигнал/шум равно 15.
элементов. Изображение передается с
частотой 25 кадров/с. Каждый элемент имеет 8 равновероятных независимых
градаций яркости. Полезный сигнал распределен по нормальному закону, отношение
сигнал/шум равно 15.
Решение:
Найдем сначала производительность источника:
![]() ,
,
![]() - энтропия одного элемента.
- энтропия одного элемента.
Тогда энтропия
кадра: ![]()
![]()
Пропускная способность канала должна быть не меньше производительности источника информации.
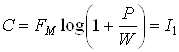 .
.
Отсюда:
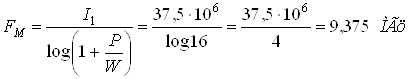 .
.
4. ЭФФЕКТИВНОЕ КОДИРОВАНИЕ СООБЩЕНИЙ
Кодирование процесс сопоставления элементов алфавита числам. Правило сопоставления называется кодом. Числа, сопоставленные элементам алфавита, называются кодовыми словами.
В зависимости
от системы счисления, положенной в основу образования чисел (кодовых слов),
различают кодирование бинарное, триарное, тетрарное и т.д. В первом случае
элементы алфавита сопоставляются бинарным числам, составленным из единиц и
нулей. Число различных элементов кода (цифр) называется его основанием ![]() (в случае бинарного кодирования
(в случае бинарного кодирования ![]() ). Число элементов кода, используемое
для представления одного элемента алфавита, называется значностью или длиной
кода. Если значность (длина) кода одинаковая для всех элементов алфавита,
то код называется равномерным.
). Число элементов кода, используемое
для представления одного элемента алфавита, называется значностью или длиной
кода. Если значность (длина) кода одинаковая для всех элементов алфавита,
то код называется равномерным.
Существует две задачи кодирования при отсутствии и наличии помех. В первом случае, ставится задача добиться кодирования элементов алфавита источника при минимальной средней значности кода, т.е. минимальным числом элементов кода в среднем на букву алфавита, при этом скорость передачи информации будет максимальной. Это достигается путем по возможности полной ликвидации избыточности сообщения. При решении данной задачи получают эффективное кодирование.
Во втором случае, ставится задача помехоустойчивого кодирования, т.е. снижения вероятности ошибок в передаче элементов алфавита, что достигается, наоборот, введением избыточности («излишних» элементов) в кодовые слова.
Вторую задачу мы рассматривать не будем. Обратимся к первой задаче. Теоретически доказывается, что минимальная средняя длина кодовых слов:
![]() ,
,
где ![]() -
энтропия источника (сообщения),
-
энтропия источника (сообщения), ![]() - основание кода.
- основание кода.
Для бинарного
кода очевидно: ![]() .
.
Отношение ![]() к реально достигнутой в данном коде
средней длине кодовых слов
к реально достигнутой в данном коде
средней длине кодовых слов ![]() :
:
![]()
называется эффективностью кода.
Качество кода
можно охарактеризовать также избыточностью кода: ![]() .
.
Средняя длина кодовых слов может быть подсчитана как:
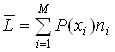 ,
,
где ![]() -
вероятность появления элементов из алфавита
-
вероятность появления элементов из алфавита ![]() в
сообщении,
в
сообщении, ![]() - длина кодового слова,
соответствующего элементу
- длина кодового слова,
соответствующего элементу ![]() .
.
При эффективном кодировании стараются добиться, чтобы средняя длина кодовых слов удовлетворяла условию:
![]() .
.
Для получения кода близкого к эффективному были разработаны алгоритмы Шеннона-Фано и Хаффмена.
Алгоритм Шеннона-Фано состоит в том, что расположенные в порядке убывания вероятностей элементы алфавита делятся на две группы по возможности равной суммарной вероятности (в каждой группе). Все элементы первой группы получают элемент «0» в качестве первой крайней слева позиции кодовых слов, а все элементы второй группы – «1». Далее подгруппы делятся на подгруппы по тому же правилу примерно равных вероятностей и в каждой подгруппе заполняется вторая слева позиция кодового слова «0»-ми и «1»-ми. Процесс повторяется до закодирования всех элементов алфавита.
Пример:
|
Элементы |
Вероятности |
Номера разбиений |
Кодовые слова |
|
|
m1 |
1/2 |
|
I II III IV V VI VII |
0 |
|
m2 |
1/4 |
|
10 |
|
|
m3 |
1/8 |
|
110 |
|
|
m4 |
1/16 |
|
1110 |
|
|
m5 |
1/32 |
|
11110 |
|
|
m6 |
1/64 |
|
111110 |
|
|
m7 |
1/128 |
|
1111110 |
|
|
m8 |
1/128 |
|
1111111 |
|
Для
данного кода: ![]() ,
, ![]() и,
следовательно,
и,
следовательно, ![]() ,
, ![]() .
.
Алгоритм Шеннона-Фано
применим и при основании кода ![]() . В этом случае
отсортированный алфавит разбивается на
. В этом случае
отсортированный алфавит разбивается на ![]() частей
примерно одинаковой суммарной вероятности.
частей
примерно одинаковой суммарной вероятности.
Алгоритм Хаффмена обеспечивает получение кодовых слов за более короткое время. Наиболее удобным является получение эффективного кода Хаффмена с помощью построения кодового дерева (хотя имеются и другие способы).
Построение графа-дерева
начинается с висячих вершин, которым в качестве весов назначают вероятности появления
элемента в сообщении ![]() . Висячие вершины
графа упорядочивают в соответствии с их весом. Это позволяет в дальнейшем
уменьшить число пересечений ребер или вовсе исключить их.
. Висячие вершины
графа упорядочивают в соответствии с их весом. Это позволяет в дальнейшем
уменьшить число пересечений ребер или вовсе исключить их.
Далее дерево строится по следующему алгоритму.
Шаг 1.
Определяется число поддеревьев графа. Если оно меньше двух, то дерево
построено и на этом действие алгоритма заканчивается. Если число поддеревьев
равно или больше двух, то осуществляется переход к шагу 2. (Замечание.
В начале построения имеется ![]() изолированных
вершин графа, являющихся поддеревьями и одновременно корнями поддеревьев.)
изолированных
вершин графа, являющихся поддеревьями и одновременно корнями поддеревьев.)
Шаг 2. Выбираются корни двух поддеревьев графа с минимальными весами и осуществляется сращивание выбранных поддеревьев с добавлением при этом одной вершины и двух ребер. Вес вновь образованной вершины определяется как сумма весов корней выбранных поддеревьев, левому добавленному ребру приписывается вес, равный нулю, правому – равный единице (или наоборот). Далее переход к шагу 1.
В результате применения алгоритма
образуется кодовое дерево – граф со взвешенными ребрами. Для получения кодового
слова элемента алфавита (или слова) ![]() достаточно
выписать веса ребер, составляющих путь из корня дерева в соответствующую
висячую вершину.
достаточно
выписать веса ребер, составляющих путь из корня дерева в соответствующую
висячую вершину.
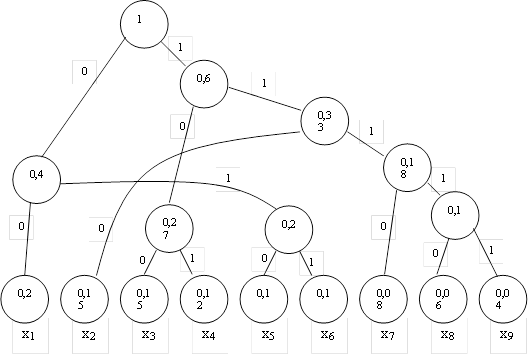
Проиллюстрируем метод Хаффмена на примере.
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
00 |
|
0,2 |
|
011 |
|
0,1 |
|
110 |
|
0,15 |
|
1110 |
|
0,08 |
|
100 |
|
0,15 |
|
11110 |
|
0,06 |
|
101 |
|
0,12 |
|
11111 |
|
0,04 |
|
010 |
|
0,1 |
|
|
|
|
Построим кодовое дерево и в соответствии с ним составим кодовую таблицу.

Характеристики
данного кода: ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Приведенные алгоритмы кодирования Шеннона-Фано и Хаффмена пригодны для кодирования независимых элементов. Если источник характеризуется зависимостью, например по-парной, то данные методики используются по отношению к парам элементов, для которых вычисляются вероятности.
Задача №1.
Источник информации задан матрицей:
 .
.
Закодировать
элементы алфавита ![]() источника информации: а)
кодом Шеннона-Фано, б) равномерным двоичным кодом. Определить основные характеристики
эффективного кода.
источника информации: а)
кодом Шеннона-Фано, б) равномерным двоичным кодом. Определить основные характеристики
эффективного кода.
Решение:
|
Сообщения |
Код Шеннона - Фано |
Равномерный код |
|
Сообщения |
Код Шеннона - Фано |
Равномерный код |
|
|
000 |
000 |
|
|
100 |
100 |
|
|
001 |
001 |
|
|
101 |
101 |
|
|
010 |
010 |
|
|
110 |
110 |
|
|
011 |
011 |
|
|
111 |
111 |
Для
равновероятных сообщений, у которых ![]() , где
, где ![]() - целое число, НДК совпадает с
оптимальным кодом.
- целое число, НДК совпадает с
оптимальным кодом.
![]()
Характеристики
кода: эффективность ![]() , избыточность
, избыточность ![]() .
.
Задача №2.
Построить код Шеннона – Фано для алфавита, элементы которого характеризуются матрицей вероятностей появления в сообщении:
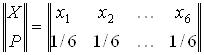 .
.
Определить характеристики кода.
Решение:
|
Сообщения |
Код Шеннона - Фано |
|
Сообщения |
Код Шеннона - Фано |
|
|
00 |
|
|
10 |
|
|
010 |
|
|
110 |
|
|
011 |
|
|
111 |
Средняя
длина кода: ![]() .
.
Энтропия
ансамбля сообщений: ![]() .
.
Эффективность
кода: ![]() .
.
Избыточность:
![]() , т.е. R=3,4%.
, т.е. R=3,4%.
Задача №3.
Построить код Шеннона – Фано для элементов алфавита с вероятностями 0,25; 0,25; 0,125; 0,125; 0,0625; 0,0625; 0,0625; 0,0625 и определить его основные характеристики.
Решение:
Кодовая таблица имеет вид
|
Сообщения |
Вероятности |
Кодовые слова |
|
Сообщения |
Вероятности |
Кодовые слова |
|
|
0,25 |
00 |
|
|
0,0625 |
1100 |
|
|
0,25 |
01 |
|
|
0,0625 |
1101 |
|
|
0,125 |
100 |
|
|
0,0625 |
1110 |
|
|
0,125 |
101 |
|
|
0,0625 |
1111 |
Средняя
значность (длина) кода: ![]() . Эффективность
кода
. Эффективность
кода ![]()
Задача №4.
Пользуясь алгоритмом Хаффмена построить для алфавита источника сообщений с вероятностями появления элементов 0,18; 0,17; 0,16; 0,15; 0,1; 0,08; 0,05; 0,05; 0,04; 0,02 : а) двоичный код; б) код с основанием 4. Определить характеристики кодов.
Решение:
а) Двоичный код.
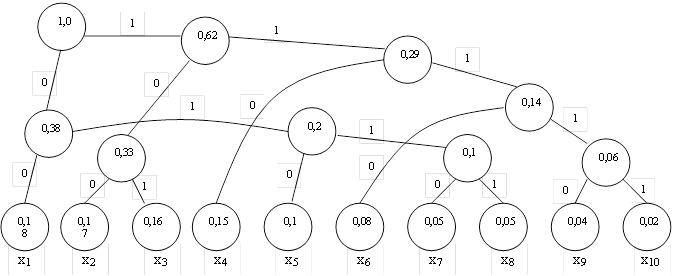

Теперь в соответствии с полученным кодовым деревом построим кодовую таблицу:
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
00 |
|
0,18 |
|
1110 |
|
0,08 |
|
100 |
|
0,17 |
|
0110 |
|
0,05 |
|
101 |
|
0,16 |
|
0111 |
|
0,05 |
|
110 |
|
0,15 |
|
11110 |
|
0,04 |
|
010 |
|
0,1 |
|
11111 |
|
0,02 |
![]() ,
, ![]() ,
,
![]() , т.е. R=2%.
, т.е. R=2%.
б) Код с основанием 4.
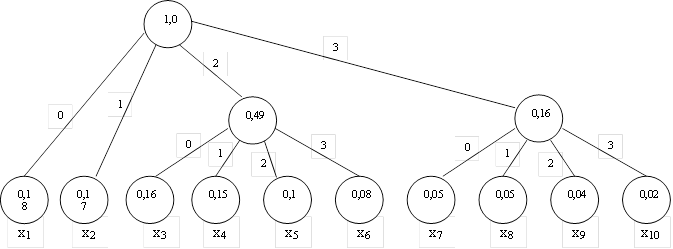

Построим кодовую таблицу:
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
0 |
|
0,18 |
|
23 |
|
0,08 |
|
1 |
|
0,17 |
|
30 |
|
0,05 |
|
20 |
|
0,16 |
|
31 |
|
0,05 |
|
21 |
|
0,15 |
|
32 |
|
0,04 |
|
22 |
|
0,1 |
|
33 |
|
0,02 |
Характеристики кода с основанием 4:
![]() ,
, ![]() ,
,
![]() , т.е. R=7%.
, т.е. R=7%.
Задача №5.
В сообщениях
используются символы алфавита ![]() с вероятностями
соответственно 0,45; 0,1; 0,15 и 0,3. Для передачи сообщения по каналу связи
могут быть применены два кода. В первом символам алфавита соответствуют кодовые
слова a, b, c, d, во втором – a, d, b,
c. Длительности передачи элементов кода по
каналу связи в условных единицах равны:
с вероятностями
соответственно 0,45; 0,1; 0,15 и 0,3. Для передачи сообщения по каналу связи
могут быть применены два кода. В первом символам алфавита соответствуют кодовые
слова a, b, c, d, во втором – a, d, b,
c. Длительности передачи элементов кода по
каналу связи в условных единицах равны: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Определить количество информации,
передаваемое каждым кодом в единицу времени (скорость передачи информации).
Предполагается, что помехи в канале связи отсутствуют. Построить эффективный код Шеннона-Фано и определить его
характеристики.
. Определить количество информации,
передаваемое каждым кодом в единицу времени (скорость передачи информации).
Предполагается, что помехи в канале связи отсутствуют. Построить эффективный код Шеннона-Фано и определить его
характеристики.
Решение:
Скорость передачи информации:
![]() , где
, где ![]() -
среднее число отправляемых элементов в единицу времени,
-
среднее число отправляемых элементов в единицу времени, ![]() -
количество информации, передаваемое по каналу связи одним элементом алфавита.
-
количество информации, передаваемое по каналу связи одним элементом алфавита.
Так как
помехи в канале отсутствуют, то ![]() . Значит:
. Значит:
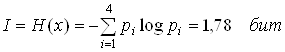 .
.
Среднее число отправляемых в единицу времени символов алфавита можно найти следующим образом:
![]() , где
, где 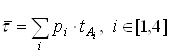 -
среднее время передачи одного символа алфавита.
-
среднее время передачи одного символа алфавита.
Для первого
кода ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
поэтому:
,
поэтому:
![]()
Для второго
кода ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
поэтому:
,
поэтому:
![]()
Таким образом, получаем:
для первого
кода ![]() ,
,
для второго
кода ![]()
Оптимальный код имеет следующий вид:
|
Сообщения |
Вероятности |
Код Шеннона – Фано |
|
|
0,45 |
0 |
|
|
0,3 |
10 |
|
|
0,15 |
110 |
|
|
0,1 |
111 |
Средняя
значность данного кода: ![]()
Эффективность
кода: ![]() .
.
Избыточность:
![]() , т.е. R=1,1%.
, т.е. R=1,1%.
Еще одна формула нахождения пропускной способности канала связи:
![]() ,
,
где ![]() –
скорость передачи элементарных сигналов (элементов кода) в секунду; h – основание кода, т.е. сколько различных элементарных
сигналов используется для передачи кодовых слов.
–
скорость передачи элементарных сигналов (элементов кода) в секунду; h – основание кода, т.е. сколько различных элементарных
сигналов используется для передачи кодовых слов.
Задача №6.
Алфавит источника сообщений состоит из 8 элементов с вероятностью появления в сообщении 0,2; 0,18; 0,16; 0,14; 0,12; 0,08; 0,07; 0,05. Построить эффективный бинарный код Хаффмена и вычислить его характеристики. Найти скорость передачи информации по каналу связи для полученного кода и пропускную способность канала, если время передачи одного двоичного элемента кодового слова t=1,25мс. Считать, что помехи при передаче отсутствуют.
Решение:
Построим кодовое дерево.
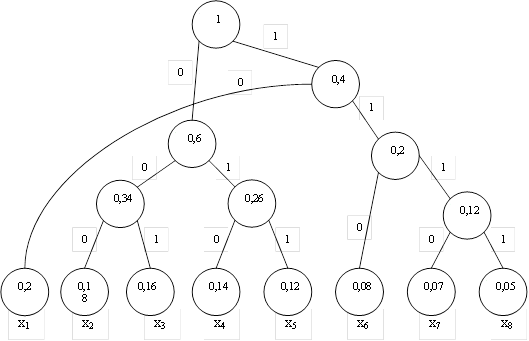

Получаем кодовую таблицу:
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
Кодовые слова |
Исходные элементы |
Вероятности |
|
10 |
|
0,2 |
|
011 |
|
0,12 |
|
000 |
|
0,18 |
|
110 |
|
0,08 |
|
001 |
|
0,16 |
|
1110 |
|
0,07 |
|
010 |
|
0,14 |
|
1111 |
|
0,05 |
Определим характеристики кода:
![]() двоичных разряда,
двоичных разряда, ![]() бит,
бит, ![]() ,
,
![]() .
.
Найдем скорость передачи информации по каналу связи при выбранном способе кодирования. Т.к. помехи в канале отсутствуют, то:
![]()
Время передачи одного символа алфавита в среднем составляет:
![]() мс
мс
Значит: ![]() симв./с
симв./с
Получаем: ![]() бит/с
бит/с
Пропускная
способность данной линии связи составляет: ![]() .
.
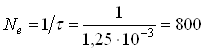 двоичн.разр./с
двоичн.разр./с
![]()
С = 800× log2 = 800 бит/с.
Получаем, что действительная скорость передачи информации не на много меньше (примерно на 1,6%), чем максимально возможная (пропускная способность линии связи).
Задача №7.
Процесс создания элементов алфавита источником информации описывается графом


На основании алгоритма Шеннона-Фано построить эффективный код и оценить его характеристики.
Решение:
Т.к. при передаче символов сообщения присутствует по-парная статистическая зависимость, то для получения кода по методу Шеннона-Фано нужно кодировать не отдельные символы, а двухбуквенные блоки. Для этого нам необходимо найти вероятности появления сочетаний букв.
Определим в начале безусловные вероятности появления отдельных символов, для этого воспользуемся формулами полной вероятности и условием нормировки:
 Получаем:
Получаем: 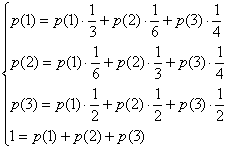
Решаем систему получаем: p(1)=1/4, p(2)=1/4, p(3)=1/2.
|
Элементы |
Вероятности |
Разбиения |
Кодовые слова |
|
x3x3 |
1/4 |
|
11 |
|
x1x3 |
1/8 |
101 |
|
|
x2x3 |
1/8 |
100 |
|
|
x3x1 |
1/8 |
011 |
|
|
x3x2 |
1/8 |
010 |
|
|
x1x1 |
1/12 |
001 |
|
|
x2x2 |
1/12 |
0001 |
|
|
x1x2 |
1/24 |
00001 |
|
|
x2x1 |
1/24 |
00000 |
Определим характеристики кода:
![]() двоичных разряда,
двоичных разряда, ![]() бит,
бит, ![]() ,
,
![]() .
.