Задача №1
Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.
Решение:
Задача №2
Имеется 5 урн, из которых две содержат по одному белому и по 5 черных шаров, одна урна – 2 белых и 5 черных шаров и последние две урны – по 3 белых и по 5 черных шаров. Наудачу выбирается одна урна и из нее наудачу извлекается один шар. Какова вероятность, что этот шар окажется белым?
Решение:
Обозначим через А1 , А2 и А3 события, состоящие в том, что шар извлечен из урны, содержащей 1, или 2, или 3 белых шара . В таком случае:
, 
,
.
Если событие В состоит в том, что извлекается белый шар, то по формуле полной вероятности, получаем:
.
Задача №3
Пусть из многолетних наблюдений за погодой известно, что для определенного пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того, что в указанный день дождя не будет, равна 0,6. Пусть далее для этого же пункта вероятность того, что 15 ноября будет идти дождь равна 0,65, вероятность, что будет идти снег – 0,15 и вероятность того, что 15 ноября вовсе не будет осадков равна 0,2. В какой из двух перечисленных дней погоду в рассматриваемом пункте следует считать более неопределенной: 1) если из всех характеристик погоды интересоваться вопросом о характере осадков; 2) если интересоваться лишь вопросом о наличии осадков.
Решение:
Согласно тому, как понимается здесь слово «погода» имела место 15 июля и 15 ноября, характеризуется следующими таблицами вероятностей:
опыт a1
|
исходы опыта |
дождь |
отсутствие осадков |
|
вероятность |
0,4 |
0,6 |
опыт a2
|
исходы опыта |
дождь |
снег |
отсутствие осадков |
|
вероятность |
0,65 |
0,15 |
0,2 |
1) Поэтому энтропии наших двух опытов равны
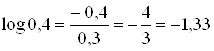
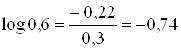
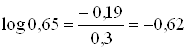
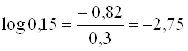
Поэтому погоду 15 ноября в рассматриваемом пункте следует считать более неопределенной, чем 15 июня.
2) Если интересоваться только тем, будут в рассматриваемый день осадки или нет, то исходы «снег» и «дождь» опыта a2 следует объединить:
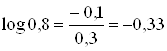
Тогда погоду 15 ноября в рассматриваемом пункте следует считать менее неопределенной, чем 15 июня.
Задача №4
На
выходе двоичного источника информации элементы «0» и «1» появляются с
вероятностями соответственно Р и (1-Р). При каком значении Р энтропия источника
максимальна? Построить график зависимости 
для
двоичного источника.
Решение:
1) Строим функциональную зависимость величины энтропии от вероятности Р:
.
Найдем значение Р, при котором данная функция принимает максимальное значение. Для этого ищем экстремум функции:
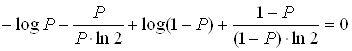
, т.о. 
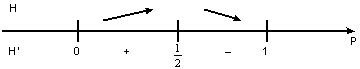
Это подтверждает свойство энтропии, что она максимальна при равновероятных элементах, т.е. Р=1/2.
2)
Зная функциональную зависимость получаем следующий
график:
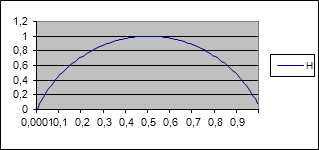
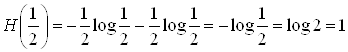
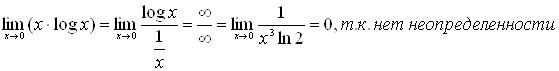
Задача №5
Имеются два дискретных троичных источника с независимыми элементами. На выходе каждого источника появляются сообщения одинаковой длины – по 15 элементов. Количество различных элементов в сообщении каждого источника постоянно. Сообщения каждого источника отличаются только порядком следования элементов, а состав сообщений постоянный. Зафиксированы два типичных сообщения: 021202120212021 – первого источника и 012101201101201 – второго. Для какого источника неопределенность появления элементов выше?
Решение:
Для первого источника:
Для второго источника:
Напомним,
что средняя условная энтропия опыта 
при условии выполнения опыта 
находится по формуле (см. лекции):
Задача №6
Определить среднюю неопределенность появления одного символа сообщения 01001000101001, при условии, что вероятность появления элементов на выходе источника информации с течением времени не изменяется, а приведенная последовательность символов – типичная.
Решение:
Задача №7
Информация передается при помощи частотно-модулированных сигналов, рабочая частота F которых изменяется с равной вероятностью в пределах от F1=10МГц до F2=50МГц. Определить энтропию значения частоты, если точность измерения частоты DF=2кГц.
Решение:
Так как
точность измерений составляет DF=2кГц, то мы имеем дело с 
числом
равновероятных исходов.
Поэтому энтропия частоты будет определяться:
Задача №8
Найти энтропию источника, описываемого графом вероятностей перехода.
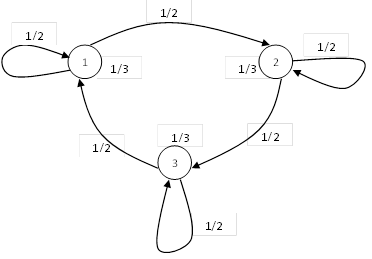
Решение:
Составляем матрицы вероятностей состояний и условных вероятностей:
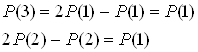
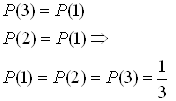
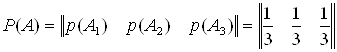
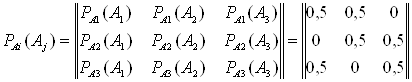
Теперь находим среднюю условную энтропию:
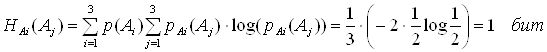
Задача №9
Измерительное устройство регистрирует временные интервалы, распределенные случайным образом в пределах от 100 до 500мс. Как изменится энтропия случайной величины при изменении точности измерения с 1мс до 1мкс?
Решение:
При точности измерения 1мс случайная величина принимает (500-100)/1=400 равновероятных значений, а значит ее энтропия:
А при точности измерения 1мкс случайная величина принимает (500-100)/0.001=400000 равновероятных значений, а значит ее энтропия:
.
Значит, энтропия случайной величины увеличится примерно на 10 бит.
Задача №10
Элементы
алфавитов X и Y статистически
связаны. Известно, что 
, 
. В каких пределах меняется условная
энтропия 
при изменении 
в
максимально возможных пределах?
Решение:
Т.к.: 
и 
, то можем
записать
.
Условная
энтропия может изменяться : 
, поэтому значения
какие будет принимать при изменении можно определить:
При
минимальном значении 
: 
.
При
максимальном значении 
: 
.
Запишем, чему равна приведенная энтропия непрерывной случайной величины, сигнала или события, подчиняющихся нормальному закону распределения:
Задача №12
В результате
полной дезорганизации управления самолеты летят произвольными курсами.
Управление восстановлено, и все самолеты взяли общий курс со
среднеквадратической ошибкой отклонения от курса 
. Найти
изменение энтропии, считая, что в первом случае имело место равномерное
распределение вероятностей углов, а во втором случае – нормальное.
Решение:
Рассмотрим каждый самолет, как случайную величину. Так, как в первом случае имеет место равномерное распределение вероятностей углов, а у нас углы изменяются от 0 до 360о, то функция распределения вероятности для одного самолета равна f(x)=1/360. Для равновероятных случайных величин:
Для первого случая:
.
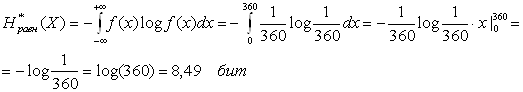Для второго случая считаем по приведенной выше формуле:
.
Таким образом изменение энтропии составит:
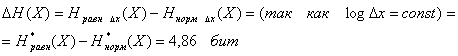
Задача №7
Избыточность ряда европейских языков лежит в пределах 50-65%. Определить энтропию их алфавитов, если считать, что число букв в алфавите европейских языков равняется 26.
Решение:
Число букв в алфавите европейских языков равняется 26,
значит максимально возможное значение его энтропии: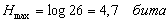 
.
Т.о. исходя из того, что:
,
можно найти энтропию алфавита: 
.
