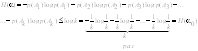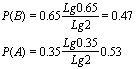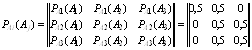1. Энтропия. Формула Шеннона

Стремление ученых дать количественную меру оценке неопределенности привели к возможности исполнения статистических подходов к построению расчетных методик, позволяющих вести количественные оценки.

Рассмотрим статистическое рассуждение, позволившее Клоду Шеннону заложить теоретические основы новой науки о информации.

Клод Шеннон предложил считать неопределенность в виде функции f, которая зависит от числа исходов k, т.е. f(k).

Если число исходов k будет равно 1, значит функция f(k)=0. Функция f(k) должна быть возрастающей функцией, если k возрастает.

Мы имеем дело со сложным опытом (). Опыт  имеет n исходов,  - m исходов. Неопределенность сложного процесса () м.б. оценена суммой  неопределенности опыта  + неопределенности опыта  

f() = f()+f().В теории информации неопределенность оценивается логарифмом по основанию 2, т.е. log₂. Единицей  неопределенности принято считать log₂2=1 – это бит. Бит – минимальное количество информации, которое соответствует неопределенности опыта, имеющего 2 исхода.

Формула Шеннона

Рассмотрим статический опыт, имеющий k равновероятных исходов. Таблица вероятностей такого опыта имеет следующий вид.

Общая неопределенность этого опыта может быть оценена величиной log k  .Каждый отдельный исход, имеющий вероятность 1/k, вносит неопределенность, равную    .

В том случае, если исходы имеют различную вероятность, (см. таблицу вероятностей),

то исходы А₁, А₂, А₃ вносят соответственно неопределенность равную:

 . В случае независимости исходов общая неопределенность опыта будет равна:.

Обобщая рассмотрение вышеизложенного можно для опыта α с таблицей вероятностей

сделать оценку в виде

В результате для опыта α мы получаем число, являющееся количественной мерой неопределенности опыта. Эта величина называется энтропией, а формула Шеннона для расчета энтропии имеет  вид:

2. Свойства энтропии

1.Энтропия не может принимать отрицательных значений:

.

 Это несложно доказать, т.к. 0£р(А)£1, а в этом интервале функция

log p(A) всегда отрицательна.

2.Энтропия H(α) равна 0 только в том случае, когда одна из вероятностей р(А₁), р(А₂),… р(А_k) равна единице, а все остальное равно 0.

Это становится очевидным, так как р(А₁) + р(А₂) + … + р(А_k) = 1, и согласно  физическому смыслу, нулевое значение энтропии возможно только в том случае, когда опыт не содержит никакой неопределенности.

3. Среди всех опытов, имеющих k исходов, наиболее неопределенным является опыт с таблицей вероятности (см.таблицу),

который принято обозначать за опыт α₀. В этом случае предсказать исход опыта труднее всего. Этому отвечает то обстоятельство, что опыт α₀ имеет наибольшую энтропию. Данное свойство довольно часто используется, а его доказательство очень громоздкое, поэтому ограничивается утверждением: если  α – произвольный опыт, имеющий k исхода (А₁, А₂, А_3,,…, А_k,), то

3.  Энтропия сложных событий

Если требуется оценить неопределенность сложных событий, например, состоящих из нескольких опытов, то необходимо иметь правила сложения энтропии.

Если мы меем дело с 2 опытами  и , имеющими таблицы вероятностей

То, в случае независимости исходов опытов, мы можем записать, что при одновременном выполнении условий опытов  и  сочетания исходов м.б. следующими:

          А₁ В₁, А₁ В₂, …, А₁ В_n

          А₂ В₁, А₂ В₂, …, А₂ В_n

……

          А_k В₁, А_k В₂, …, А_k В_n

Следовательно, в этом случае Н() = Н()+Н()

Если исходы опытов зависят друг от друга, то энтропия такого сложного опыта записывается по другой формуле Н() = Н()+Н ()

Н ()- условная энтропия (энтропия  при условии выполнения )

Н () = Р (А₁) Н _А1 () + Р (А₂) Н _А2 () + … + Р (А_к) Н _Ак ()

4. Свойства условной энтропии

1. Очень существенно, что условная энтропия Н_α(β) заключается между нулем и энтропией Н(β) (безусловной):

                                    .

Это свойство хорошо согласуется со смыслом энтропии как меры неопределенности. Очевидно, что предварительное выполнение опыта α может лишь уменьшить степень неопределенности β, а в случае независимости опытов α и β степень неопределенности не изменится. Однако опыт  α не может увеличить неопределенность опыта β.

2. Второе свойство =0

Если опыт  действительно имеет вероятности исходов = Р (А₁), Р (А₂), …, Р (А_к) и сумма этих вероятностей = 1, то  = 0, если все величины Н _А1 () = Н _А2 () = … = Н _Ак () = 0

Суммарная энтропия такого опыта Н() = Н()

Если мы имеем также вероятности исходов опыта  (Р()), то в этом случае величины энтропии опыта  при условии опыта  в сумме будут стремиться к энтропии Н(), т.е. в этом случае мы приходим к формуле суммирования энтропий независимых опытов.

3. Третье свойство:

учитывая, что опыты  и  ничем не отличаются друг от друга в своей постановке Н()=Н() следовательно: Н()+Н ()=Н()+Н ()

5.Информация в сложном опыте

Основой современного представления о информации является энтропия. Если исследуемый объект, не содержит информации, то очевидно, что его энтропия = 0.

Предположим, что опыту  имеющему энтропию Н() предшествует опыт . Очевидно, что в некоторых случаях опыт  может снизить энтропию опыта .

Если опыты  и  связаны между собой, то это обстоятельство может привести к уменьшению энтропии , причем, если опыт  полностью исчерпает неопределенность опыта , то Н() м.б. = 0. если же опыт  и  не связаны между собой, то Н() останется без изменений. В этом случае мы не получим никакой информации.

Исходя из этих рассуждений, можем записать, что информация

I() = Н() - Н  ()

Данное определение является не единственным определением информации, но его удобство заключается в том, что при исследовании мы получаем информацию, используя вспомогательные понятия или опыт.

6. Свойства информации

1.Информация относительно опыта b, содержащаяся в опыте α, всегда равна информации относительно α, содержащейся в b.

Это непосредственно следует из соотношений:

Н(b) - Н_α(b)=Н(α)  - Н_b(α).

Следовательно,

I(α,b) = Н(b) – Н_α (b) = Н(α) – Н_b(α) = I(b,α).

Таким образом, информацию I(α,b), которую содержит опыт α относительно b, можно назвать взаимной информацией двух опытов α и b относительно друг друга.

2.Информация I(α,b), содержащая в опыте α относительно опыта b, не превосходит энтропию Н(α) опыта α. Это свойство не требует доказательства, так как

I(α, b) = Н (α) – Н_b (α).

3.Информация I(α,b) точно равна энтропии Н(α) только в том случае, когда условная энтропия Н_b(α) точно равна нулю, т.е. результат опыта α, полностью определяет исход вспомогательного опыта b.

4. Если опыты α и b независимы, то информация I(α,b)=0

К более общим свойствам информации можно отнести следующие ее свойства:

1. Информация не материальна, но она проявляется в форме материальных носителей – дискетных знаков или символов.

2. Информация может быть заключена как в знаках, так и в их взаимном расположении.

3. Знаки и символы несут информацию только для получателя способного их распознать. Распознание состоит в соответствии знаков и символов с объектами и их отношениями в реальном мире. Поэтому информацию можно определить как результат моделирования реального мира.

Сигналами принято называть динамические процессы изменения во времени  величины любой природы: тока, напряжения, излучения, звука и т.д.

Знаками будем называть различимые получателем реальные объекты: буквы, цифры, символы.

7.  Избыточность в языке

При определении H₁=H(a₁) – энтропии опыта по оценке неопределенности, содержащейся в одной букве алфавита, мы считали, что буква независима. Это означает, что при составлении сообщения, в котором каждая буква содержит 4,35 бит информации, можно прибегнуть к помощи урны, в которой лежат тщательно перемешанные 1000 бумажек, из которых  175 не содержат ничего («пробел»), на 90 написана буква «О», на 72 – «Е» и т.д. Извлекая из такой урны бумажки, мы получим ничего не значащую фразу. Эта фраза будет похожа на русскую речь, но будет очень далека от разумного текста. Несходство полученной фразы с осмысленным сообщением объясняется тем, что на самом деле буквы в тексте не независимы друг от друга. Так, например, если мы знаем, что очередной буквой явилась гласная, то значительно возрастает вероятность появления на следующем месте согласной буквы и т.д.

Наличие в русском тексте определенных закономерностей приводит к дальнейшему уменьшению степени неопределенности одной буквы сообщения. Количественно это уменьшение можно оценить использованием условной энтропии H₂ = H_a1(a₂), которая является

энтропией опыта a₂, состоящего в определении одной буквы текста при условии, что нам известен исход опыта a₁, состоящего в определении предшествующей буквы.

Таким образом, особенности языка вносят определенную зависимость опытов, отражающихся в энтропии.

Известно, что с возрастанием числа букв в словах сообщения энтропия одной буквы уменьшается.  К.Шенноном введено понятие избыточности языка:

 ,

где – предельное значение энтропии с учетом

вероятности сочетаний букв в словах сообщения, H₀ – средняя неопределенность букв (в русском алфавите H₀ = 4,35 бит).

Применительно к русскому языку избыточность заметно превышает 50 %. Это обстоятельство объясняется тем, что выбор следующей буквы осмысленного текста более, чем на 50 % определяется самой структурой языка и, следовательно, случаен лишь в сравнительно небольшой степени. Именно избыточность языка позволяет сокращать телеграфный текст за счет отбрасывания некоторых легко отгадываемых слов, предлогов, союзов. Она же позволяет легко восстанавливать истинный текст даже при наличии значительного числа ошибок в телеграмме или описок в книге.

Н = , где  статистический опыт, заключающийся в результате отгадывания буквы при условии, что нам известна какой была предыдущая буква, т.е. нам известен результат предыдущего опыта _1.

8. Код Шеннона-Фано

  Идея использования неравенства H < log n для построения экономичного кода очень эффективно используется в кодах, которые впервые предложили в 1948 – 1949 гг.  Р. Фано и К. Шеннон.

            Предположим, что алфавит содержит n букв. Расположим буквы алфавита в один столбик в порядке убывания вероятностей. Затем разобьем их на две группы – верхнюю и нижнюю. Для букв первой группы в качестве первой цифры кодового обозначения используем 1, а для букв второй группы – цифру 0. Далее, каждую из двух полученных групп снова разделим на две части с возможно более близкой суммарной вероятностью. В качестве второй цифры кодового обозначения используются цифры 1 и 0 в зависимости от того, принадлежит ли буква к первой или второй из этих подгрупп. Затем каждая из содержащих более одной буквы групп снова делится на две части и т.д. Процесс повторяется до тех пор, пока каждая из разделенных групп будет содержать по одной букве.

            Рассмотрим несложный принцип кодирования по методу Шеннона–Фано. Допустим, что алфавит содержит всего шесть букв, вероятности которых в порядке убывания равны 0,4; 0,2; 0,2; 0,1; 0,05; 0,05 (см. таблицу).

Основной принцип, положенный в основу кодирования по методу Шеннона-Фано заключается в том, что при выборе каждой цифры кодового обозначения стараются, чтобы содержащаяся в ней информация была наибольшей. Разумеется, количество цифр в различных обозначениях будет неодинаковым, то есть код Шеннона-Фано является неравномерным. Буквы, имеющие большую вероятность, получают более короткие обозначения, чем соответствующие маловероятные буквы. В результате, хотя некоторые кодовые обозначения здесь и могут иметь весьма значительную длину, среднее значение длины такого обозначения значительно уменьшается.

9. Анализ экономичности кода

В нашем примере шестибуквенного алфавита равномерный код состоит из трехзначных кодовых обозначений ( так как 2² < 6 < 2³ ). На каждую букву в лучшем случае приходится три сигнала. При использовании кода Шеннона-Фано среднее значение числа элементарных сигналов, приходящихся на одну букву сообщения, будет равно (данные берем из таблицы кодирования по методу Шеннона-Фано 8вопрос):

1´0,4 + 2´0,2 + 3´0,2 + 4´0,1 + 5´ (0,05 + 0,05) = 2,3 .

            Это значительно меньше, чем 3, и не очень далеко от значения энтропии Н:Н = –0,4´ log 0,4 – 2´0,2´ log 0,2 – 0,1´log 0,1 – 2´0,05´log 0,05 = 2,22.

     Если провести аналогичный анализ для алфавита, состоящего из 18 букв, то равномерный код будет иметь пятизначное кодовое обозначение, а код Шеннона-Фано будет иметь буквы даже с семью двоичными сигналами, но зато среднее число элементарных сигналов, приходящихся на одну букву, будет равно 3,29 и это немного отличается от величины энтропии Н = 3,25. Особенно выгодно кодировать по методу Шеннона-Фано не отдельные буквы, а сразу целые блоки из нескольких букв. Даже в неблагоприятных случаях кодирование целыми блоками позволяет приближаться к величине энтропии. Рассмотрим пример, когда имеются лишь две буквы А и Б с вероятностями р(А) = 0,7 и р(Б) = 0,3.

Тогда                Н = –0,7 log0,7 – 0,3 log0,3 = 0,881 .

     Применение метода Шеннона-Фано к исходному двухбуквенному алфавиту здесь оказывается бесцельным. Он приводит нас к простейшему равномерному коду, требующему для передачи одного двоичного знака.

Здесь мы имеем превышение Н на 12 %. Если применить код Шеннона-Фано к кодированию всевозможных буквенных сочетаний, то

среднее значение длины кодового обозначения в этом случае  1´0,49 + 2´0,21 + 3´0,21 + 3´0,09 = 1,81 .

     На одну букву приходится 1,81 / 2 = 0,905, что лишь на 3% больше Н = 0,881 бит. При использовании трехбуквенных комбинаций средняя длина кодового обозначения 2,686, то есть на одну букву приходится 0,895 двоичных знаков, что всего на 1,5% больше Н.     Рассмотренные примеры анализа степени близости среднего числа двоичных знаков, приходящихся на одну букву сообщения, к значению Н может быть увеличено при помощи перехода к кодированию еще более длинных блоков. Этому обстоятельству посвящена основная теорема кодирования.

Теорема: При кодировании сообщения, разбитого на N–буквенные блоки, можно, выбрав N достаточно большим, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близким к Н.

10. Анализ двоичной симметричной линии

Пусть по линии связи передается два элементарных сигнала (А₁ – импульс, А₂ – пауза). Вероятность безошибочного приема любого из передаваемых сигналов примем за 1–р, а вероятность ошибки будет равна р. В этом случае р_А1(А₁) = р_А2(А₂) = 1–р, а  р_А1(А₂) = р_А2(А₁) = р.

Графически схему двоичной симметричной линии принято изображать согласно схеме (рис.13). На рис.13, а   отражена конфигурация передаваемого сигнала, а на рис.13,б показано, в какие принимаемые сигналы могут перейти передаваемые сигналы А₁ и А₂ и с какой вероятностью              

Рис. 13. Схема двоичной симметричной линии: а - характер

сигналов А₁ и А₂;   б - схема преобразования сигналов. Для вычисления величины с воспользуемся равенством

I(a, b) = H (b) – H_a (b) .

Из схемы (рис.13,б) видно, что если передается сигнал А₁, то на приемном конце с вероятностью 1–р получим тот же сигнал А₁, а с вероятностью р – сигнал А₂. Аналогично с передачей сигнала А₂. Потому

Н_А1(b) = Н_А2(b) = – (1–p) log (1–p) – p log p;

     H_a (b) = p(A₁) H_A1(b) + p(A₂) H_A2(b) = – (1–p) log (1–p) – p log p,

так как р(А₁) + р(А₂) = 1.

Отсюда легко сделать вывод о том, что в рассматриваемом случае

H_a (b) не зависит от вероятностей р(А₁) и р(А₂), и для вычисления с = max I(a, b) = max[H (b) – H_a (b)] надо определить только максимальное значение H (b). Величина H (b) – энтропии опыта b, имеющего только два исхода (рис.13, а) и поэтому  она не превосходит одного бита. Значение

H(b) = 1 достигается при р(А₁) = р(А₂) = 0,5, так как в этом случае оба исхода b будут равновероятными. В рассматриваемом случае  р⁰(А₁) =  р⁰(А₂) = 0,5,

с = 1 +  (1–p) log (1–p) + p log p.

Следовательно, искомая пропускная способность двоичной симметричной линии будет равна

С = L[1 +  (1–p) log (1–p) + p log p].

Последняя формула показывает, как пропускная способность двоичной симметричной линии зависит от вероятности ошибки р.

Рис. 14. Зависимость пропускной способности двоичной симметричной линии от вероятности ошибки

Наибольшее значение C = L функция достигает при р = 0 (помехи отсутствуют) и р = 1 (А₁ ® А₂, А₂ ® А₁) помеха не мешает понять какой сигнал был передан. При р = 0,5 пропускная способность линии равна нулю. Независимо от того, какой сигнал был передан, мы получим на приемном конце с вероятностью 0,5 сигнал А₁ и с вероятностью 0,5 сигнал А₂. Принятый сигнал не будет содержать никакой информации.

11. Марковские процессы. Разновидностью случайных процессов является Марковский процесс.

Пространство состояния дискретного Марковского процесса представляет собой конечное или счетное множество, которое может быть отождествлено с помощью не отрицательных чисел.

Дискретный Марковский процесс с дискретным временем называется цепью Маркова. Характеризуется тем, что переход от одного состояния в другое возможно лишь в дискретные моменты времени t₀, t_1,  t₂, … При этом абсолютное значение времени роли не играет. Поэтому обычно временной параметр Т отождествляется с множеством индексов {1, 2, 3, …}. И тогда цепь Маркова имеет вид x₀, x₁, x₂, …При определенной зависимости случайных величин x_i случайная величина принимает значение из множества L : L= {1,2,3,…} i=0,1,2,.. Частным случаем цепи Маркова может служить последовательность x₀, x₁, x₂, …полученная путем независимых испытаний с исходами 1, 2, 3, …

Каждому исходу j сопоставлена вероятность P_j его появления в независимом опыте. В этом случае вероятность появления при n независимом испытании конкретной последовательности исходов j₀, j₁, j₂,… равна произведению вероятностей этих исходов P{(x₀=j₀), (x₁=j₁), …, (x_n=j_n)}=P_j0* P_j1* P_j2*…* P_jn Цепь Маркова является простейшим обобщением рассматриваемой схемы независимых испытаний, которая заключается в допущении зависимости исхода любого испытания от исхода предыдущего испытания. Отсюда следует, что для описания последовательности x₀, x₁, x₂, … надо задать распределение вероятности {P_j}  первого испытания x₀ и всем парам вида (j,k) сопоставлять условные вероятности P_jk.

Вероятность появления конкретной последовательности j₀, j₁, j₂, …, j_n с учетом указанного допущения равна произведению вероятностей P{(x₀=j₀), (x₁=j₁), …, (x_n=j_n)}=P_j0* P_j0j1* P_j1j2*…* P_jn-1jn

Еще одно обобщение в схемах независимых испытаний приводящее к цепи Маркова, но некоторого общего характера основанного на допущении, что исход любого испытания зависит не только от исхода предыдущего испытания но и от порядного номера предыдущего испытания. Итак, представим, что цепь Маркова описывает некоторую систему с дискретными состояниями. Если система в момент времени n находилась в состоянии j то вероятность перехода в состояние к в момент времени j+1 зависит в общем случае от значения n, j, k и независим от того в каких состояниях система прибывала в более ранее, чем n моменты времени. Это свойство получившее название Марковского позволяет определить цепь Маркова через условные вероятности P_jk(n, n+1) Это вероятность того, что система перейдет в состояние к  в момент времени n+1. Если она в момент времени n находилась в состоянии j.

Если в момент времени n система находилась в состоянии j, а в момент n+m она перешла в состояние к то говорят о переходе системы из состояния к за m шагов. Вероятность такого перехода P_jk(n, n+m)=P_jk(m)

Вероятность такого перехода P_jk(n, n+m) называется m-шаговой переходной вероятностью.

Цепь Маркова является однородной, если переходные вероятности независят от времени. Для однородной цепи Маркова вероятность P_jk(n, n+m)=P_jk(m). Вероятность P_jk(1) перехода состояния j в состояние к будем обозначать P_jk.

При описании цепи Маркова P_jk удобно записывать в виде матрицы

Данную матрицу называют матрицей вероятностей перехода цепей Маркова. В этой матрице j-строка (при j=1…n) представляет собой распределение вероятностей случайной величины при условии если x_n=j. Отсюда следует что сумма вероятностей в каждой строке матрицы=1. Т.о. матрица вероятностей перехода есть квадратная матрица с неотрицательными, не превышающими  единицу элементами, образующими по строкам единичную сумму.

12. Принцип цепей Маркова.            В теории информации источники дискретных сообщений иногда рассматриваются как генераторы последовательности символов из некоторого алфавита. L= {x­₁, x₂, x₃, …, x_n}. Если зависимость между символами последовательности простирается не более чем на пару соседних символов, то такие последовательности являются цепями Маркова.

         Пусть алфавит L={0,1} то тогда сообщения дискретного источника может быть описано матрицей.

, где Р₀₀ и Р₁₁ вероятности того, что за принятым символом следует тот же самый, соответственно 0 или 1. А P₀₁ и P₁₀ это вероятности того что следующий символ будет отличен от принятого 0 или 1.

С помощью цепей Маркова могут быть описаны так называемые процессы гибели и размножения. Используем в качестве модели для исследования численности популяции. Следуя этой модели система находится в состоянии j, если число членов популяции равно  j, рождение одного члена популяции соответствует переход системы в состояние j+1, а гибель одного члена j-1. В данной модели делаются допущения, что система за 1 шаг не может перейти из состояния j в состояние j±k если к>1 при увеличении численности популяции условия ее существования изменяются и, следовательно, вероятности перехода системы из состояния j в состояние j+1 или j-1 будут зависеть в общем случае от j.

Введем обозначения для вероятности перехода

Состояние системы j=0 соответствует полному отсутствию членов популяции. Вероятность a₀- рождение одного члена популяции обычно принимается > 0.

Матрица вероятностей перехода будет иметь вид

   C₀      a₀      0     0 …………………....0

   b₁       c₁      a₁     0…………………….0

 P=    0       b₁      c₁     a₁… ……….………..0

   ……………………………………..

   0      0…………………… b_j      c_j     a_j

Процесс гибели и размножения иногда исследуется при ограничении max численности популяции. Матрица переходов в этом случае становится конечной. Например при достижение численности =4 размножение прекращается.

                           C₀       a₀        0       0      0

                           b₁        c₁        a₁       0       0

        P=               0        b₂         c₂       a₂      0

                            0        0       b₃       c₃       a₃    

                            0        0       0       b₄       c₄          

                              ……………………….

13. Дискретный Марковский процесс с непрерывным временем. Такой проц относится к типу случайных процессов с дискретным множеством возможных состояний L  и непрерывным временным пар-ом  . В отличае от цепей М-о дискретный М-й про-с с непрер-м вр-м может переходить из состояния в сост-е не в строго фиксированный а в любой момент вр t. При этом предпологая, что переходы осущест-я мгновенно. Рис: Реализация дискр-го случ-го проц-а с непрерывным вр-м.

На рис изображена возможная реализация диск-го случ-го про-а принимающая 3 возможных вариантных состояния. Точками на оси абсцисс отмечены мом-ы вр соответс-е переходам проц-а из сост-я в сост-е. Эти моменты заранее неизв-ны. Их совокупность можно рассматривать как случайный поток событий. Для исследования дис-го М-го проц-а с непрер-м вр может оказаться полезным представления связывающие каждое сост-е проц-са с отдельным управляю-м потоком случ-х событий. Каждый поток может обладать своими собст-ми харрак-ми. Очередное событие поступающее в j-м потоке приводит процесс в некоторое из возможных сост-й лишь в том случае, если перед этим он находился в j-ом сост-и. k-й поток переводит поток из k-го сост и т.д. Напр: на рис моменты вр  t2,t5,t7 есть  подмнож-во моментов вр образующих управленческий поток связанный с уходом из сост 2. Дискр-й М-й про-с  с непр-м вр полагает жеские ограничения на хар-ки управл-х потоков. Это ограничение диктуется М-м св-ом. Если обозначить сост проц в мом-т вр t  чкркз x(t) то М-е св-во запишется: вероятность p_jk(to;t)=p{X(t)=k(X(t0))=j}. Это вероя-ть зав от to,t и k, т.е. вер-ть того, что проц в некот-й мом-т вр t>t0 будет нах-ся в сост k, зависит лишь от настоящего мом-а вр t0 и от сост j  в кот-м  проц нах-я в данный мом. Следует обратить внимание на то, что вер-ть p_jk от (t0,t) не зависит от того как протекал проц-с до мом вр t0. В частности от того как долго проц-с нах-я в сост j до наст-о вр  t0. Вр пребывания проц-а в некотором j-м сост tj есть случ вел-на (с/в) и ясно , что она полностью определ-я хар-ми управленческого потока. В силу М-го св-ва распределение остаточного вр  прибывания проц в сост j должно зависить только от сост j и не должно зав-ть от того как долго проц-с уже нахо-ся в сост j. Определимся с требованиями к управляющ-му потоку. Пусть с/в t с плотностью распред-я  fj(t)  есть вр пребывания М-о проц в j-ом сост . Рассм поток случ соб-й Пj интервалы м/д соседними сост кот также распред-ы по fj(t). Реализацию подобного потока можно получить из реализ-ции суммарного потока(из рис напр j=2). Если составлять интервал м/д соседними соб-си потока П2 отрезками вр длины [t2-t1],[t5-t4],[t7-t6]. Предположим, что мы начали наблюдать за М-и проц с произ-го мом вр t0, когда  он находился в сост j. Это эквивал-но тому, что по оси вр с изображ-ми на ней потоками Пj случайным образом отмечена точка t0

Точка t0 попадает на некот интервал вр  кот явл с/в. Вр до наступления след-го события в потоке Пj это с/в кот соотв-т остаточному вр пребывания М-о проц в сост j. Управл-й j-й поток должен обладать такими хар-ми что бы обусловленное его существование вр пребывания система в j-ом сост Tj и остаточное вр пребывания в том же сост  подчинялось одному и тому же зак-ну распределения, т.е. если qj()-это плотность расп-я от , то при  любых =t будет выполн-ся след-е рав-во  Сущ-т док-во, что для того, чтобы остаточное вр пребывания М-го проц с непр вр в j-ом сост независило от того сколько вр проц уже пребывал в этом сост, вр преб проц в j-ом сост должно подчиняться показат-му зак-у распр-я такой поток наз-я пуассоновским .

14. Уравнение Колмагорова Рассмотрим Марковские свойства дискретных процессов управляемых нестационарными Пуассоновскими потоками. Пусть имеется система с N возможными составляющими, динамика которой описывается Марковским процессом с непрерывным временем. При исследовании подобных систем в первую очередь ставится задача вычисления вероятностей состояния системы . На основе распределения  можно найти все остальные характеристики системы. Это законы распределения времени пребывания системы в том или ином состоянии, среднее время пребывание системы в определённом состоянии и т.д.

Используем основное преимущество Марковских процессов с непрерывным временем исследования, заключающееся в том, что распределение вероятностей , находится из решения системы обыкновенных линейных дифференциальных уравнений. Рассмотрим методику составления таких уравнений, будем считать, что с каждым состоянием j системы связан Пуассоновский поток с интенсивностью . Вероятность  того, что система, находящаяся в состоянии j в момент времени t не перейдёт в другое состояние за малый интервал времени , примыкающий к моменту t,  равна вероятности того, что в управляющем j-м потоке на интервале   не наступит ни одного события:

, при достаточно малом промежутке времени,тогда, вероятность в сумме с вероятностью того, что система перейдёт из состояния j за время в другое состояние составляет полную группу событий, отсюда следует, что вероятность перехода из состояния j в другое состояние равна  .

Обозначим через условную вероятность перехода из состояния j в состояние k (jk), при условии появления события в j-м управляющем потоке, тогда вероятность перехода из состояния j в состояние k за время будет равна:  , воспользовавшись формулой полной вероятности, можно записать выражение для вычисления безусловной вероятности того, что система в момент времени  будет находиться в состоянии k и эта вероятность равна:

. Проведя  преобразования, получим , при  получаем дифференциальное уравнение , данное уравнение было выведено Колмагоровым, оно показывает, как изменяются вероятности состояния системы с течением времени. Если ввести нулевые начальные условия, то уравнение Колмагорова принимает вид: .Существует методический приём, позволяющий довольно просто получать уравнения на основе анализа графа состояний системы, рассмотрим в качестве примера граф: Рис.          Система допускает любые переходы из состояния 1,2,3,4. На каждой дуге j_k прописан вес , т.е. интенсивность потока случайных событий, переводящих систему из состояния j в состояние k, очевидно, что если состоянием j управляет поток с интенсивностью   и условная вероятность перехода из состояния j в состояние k равна , то .             Существует простое мнимоническое условие для составления системы дифференциальных уравнений. Производная  вероятности того, что система будет пребывать в состоянии x_i, равна алгебраической сумме нескольких членов. Число членов этой суммы равно числу стрелок на графе состояний системы, соединяющих состояние x_i с другими состояниями, если стрелка направлена к состоянию x_i,  то соответствующий член берётся со знаком «+», наоборот – со знаком «-».Каждый член суммы равен произведению вероятностей того состояния,  от которого направлена стрелка на интенсивность потока события, переводящего систему по данной стрелке. Число отрицательных членов должно быть равно числу стрелок, направленных от состояний x_i, число положительных членов, соответственно, равно числу стрелок, направленных к x_i.

19. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.

Решение

А-допущена ошибка в 1

Р(А)=0,4

Р()=0,6

В- допущена ошибка во 2

Р(В)=0,4

Р()=0,6

С- допущена ошибка в 3

Р(С)=0,4

Р()=0,6

Р=

25.  Информация передается при помощи частотно-модулированных сигналов, рабочая частота F которых изменяется с равной вероятностью в пределах от F1=10МГц до F2=50МГц. Определить энтропию частоты, если точность измерения частоты DF=2кГц.

Решение:

Так как точность измерений составляет DF=2кГц, то мы имеем дело с (F2-F1)/DF числом равновероятных исходов. Поэтому энтропия частоты будет определяться:

20. Имеется 5 урн, из которых две содержат по одному белому и по  5 черных шаров, одна урна – 2 белых и 5 черных шаров и последние две урны – по 3 белых и по 5 черных шаров. Наудачу выбирается одна урна и из нее наудачу извлекается один шар. Какова вероятность, что этот шар окажется белым?

Решение:

Обозначим через А₁ , А₂  и А₃  события, состоящие в том, что шар извлечен из урны, содержащей 1, или 2, или 3 белых шара . В таком случае:

, ,.

Если событие В состоит в том, что извлекается белый шар, то по формуле полной вероятности, получаем:

.

21. Пусть из многолетних наблюдений за погодой известно, что для определенного пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того, что в указанный день дождя не будет, равна 0,6. Пусть далее для этого же пункта вероятность того, что 15 ноября будет идти дождь равна 0,65, вероятность, что будет идти снег – 0,15 и вероятность того, что 15 ноября вовсе не будет осадков равна 0,2. В какой из двух перечисленных дней погоду в рассматриваемом пункте следует считать более неопределенной если: 1) из всех характеристик погоды интересоваться вопросом о характере осадков; 2) если интересоваться лишь вопросом о наличии осадков.

Решение:

Согласно тому, как понимается здесь слово «погода» имела место 15 июля и 15 ноября, характеризуется следующими таблицами вероятностей:

опыт a₁

опыт a₂

1) Поэтому энтропии наших двух опытов равны

Поэтому погоду 15 ноября в рассматриваемом пункте следует считать более неопределенной, чем 15 июня.

2) Если интересоваться только тем, будут в рассматриваемый день осадки или нет, то исходы «снег» и «дождь» опыта a₂ следует объединить:

Тогда погоду 15 ноября в рассматриваемом пункте следует считать менее неопределенной, чем 15 июня.

22.  На выходе двоичного источника  информации элементы «0» и «1» появляются с вероятностями соответственно Р и (1-Р). При каком значении Р энтропия источника максимальна? Построить график  для двоичного источника.

Решение:

1) Строим функциональную зависимость величины энтропии от вероятности Р:

.

Найдем значение Р, при котором данная функция принимает максимальное значение. Для этого ищем экстремум функции:

, т.о.

Это подтверждает свойство энтропии, что она максимальна при равновероятных элементах источника.

2) Зная функциональную зависимость  получаем следующий график:

23.  Имеются два дискретных троичных источника с независимыми элементами. На выходе каждого источника появляются сообщения одинаковой длины – по 15 элементов. Количество различных элементов в сообщении каждого источника постоянно. Сообщения каждого источника отличаются только порядком элементов. Зафиксированы два типичных сообщения: 021202120212021 – первого источника и 012101201101201 – второго. Элемент какого источника несет в среднем большее количество информации?

Решение

1.

2. 

---=1,53 бит

---=1,500 бит

24.  Определить среднее количество информации приходящейся на один символ сообщения 01001000101001, при условии, что источник эргодический, а последовательность – типичная.

Решение:

01 00 10 00 10 10 01

Источник – эргодический

Последовательность – типичная

Всего 14 символов, 0-9 и 1-5

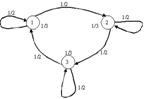
26.  Найти энтропию источника, описываемого графом вероятностей перехода:

Решение:

Составляем матрицы вероятностей состояний и условных вероятностей:

Теперь находим среднюю условную энтропию:

27. Измерительное устройство вырабатывает временные интервалы, распределенные случайным образом в пределах от 100 до 500мс. Как изменится энтропия случайной величины при изменении точности измерения с 1мс до 1мкс?

Решение:?

28. Элементы алфавитов X и Y статистически связаны. Известно, что , . В каких пределах меняется условная энтропия  при изменении  в максимально возможных пределах?

Решение:

Согласно (4.9) мы  можем записать

.

Условная энтропия может изменяться (4.7): , поэтому значения , которые она будет принимать при изменении , можно определить:

.

При минимальном значении : .

При максимальном значении : .

29.  В результате полной дезорганизации управления m самолетов летят произвольными курсами. Управление восстановлено, и все самолеты взяли общий курс со среднеквадратической ошибкой отклонения от курса . Найти изменение энтропии, считая, что в первом случае имело место равномерное распределение вероятностей углов, а во втором случае – нормальное.

Решение:

Рассмотрим каждый самолет, как случайную величину. Так, как в первом случае имеет место равномерное распределение вероятностей углов, а у нас углы изменяются от 0 до 360^о, то функция распределения вероятности для одного самолета равна f(x)=1/360.

Для равновероятных случайных величин:

.

Для второго случая считаем по формуле (4.11):

Таким образом изменение энтропии составит:

30. Избыточность ряда европейских языков лежит в пределах 50-65%. Определить энтропию их алфавитов.

Решение:

Число букв в алфавите европейских языков равняется 26, значит  максимально возможное значение его энтропии: .

Т.о. исходя, что:

можно найти энтропию алфавита:

.