Вопрос 26. Классификация имитационных моделей. Тактическое планирование имитационного эксперимента.

 

Область применения и классификация имитационных моделей

 

Первый шаг к созданию имитационной модели состоит в описании реально существующей системы с использованием характеристик основных событий. Событие определяется как точка во времени, в которой происходят изменения характеристик системы. Обычно изменения имеют место в тех случаях, когда кончается один процесс (или несколько процессов) и начинаются другие. Для получения требуемых результатов моделирования достаточно наблюдать систе­му в те моменты, когда происходят события.

Успех имитационного моделирования сложных систем непосред­ственно связан с теми успехами, которые достигнуты в последние го­ды в области совершенствования цифровых ЭВМ. Хотя вычисления при имитационном моделировании просты, они требуют больших затрат времени. Сходимость метода Монте-Карло порядка  (достаточно медленная).

 

Применение имитационного моделирования целесообразно в следующих случаях:

1)         если не существует законченной постановки задачи на исследование и идет
процесс познания объекта моделирования;

2)         если характер протекающих в системе процессов не позволяет описать эти
процессы в аналитической форме;

3)         если необходимо наблюдать за поведением системы (или отдельных ее  ком-­
понентов) в течение определенного периода, в том числе с изменением скорости
протекания процессов;

4)         при изучении новых ситуаций в системе либо при оценке функционирования
ее в новых условиях;

5)         если исследуемая система является элементом более сложной системы,  дру-
гие элементы которой имеют реальное воплощение;

 6) когда необходимо исследовать поведение системы при введении в нее новых
компонентов;

7) при подготовке специалистов и освоении новой техники (в качестве три
нажеров).

  Приведенный список возможных областей применения имитационных мо-

делей одновременно можно рассматривать и как перечень их достоинств. К сожалению, имитационные модели имеют целый ряд недостатков.

Первый, и весьма существенный, заключается в том, что разра­ботка ИМ, как правило, требует больших затрат времени и сил. Кроме того, любая имитационная модель сложной системы значительно менее объективна, чем аналитическая модель, поскольку она прежде всего отражает субъективные представления разработчика о моделируемой системе. Причем достаточно сложно как опровергнуть, так и обосновать адекватность создан­ной ИМ, особенно если речь идет о проектируемой системе. И, наконец, результаты имитационного моделирования, как и при любом численном методе, всегда носят частный характер. Для получения обоснованных выводов необходимо проведение серии модельных экспериментов, а обработка результатов требует применения специальных статистических процедур. Ниже представлено дерево классификации имитационных моделей.

 

 

 

Рис. 4.2. Классификация имитационных моделей

 

Наиболее важный признак имитационной модели — способ представления в модели динамики (дви­жения) системы. Она может быть описана посредством событий, работ (активно­стей), процессов и транзактов.

 

Другой важный признак — способ изменения модельного времени. По этому признаку различают моделирование с постоянным шагом и моделирование по осо­бым состояниям.

Все эти понятия являются основополагающими в теории имитационного моде­лирования.

В большинстве случаев конечной целью моделирования является оптимизация тех или иных параметров системы. Однако, как было отмечено выше, потенциаль­ные возможности имитационного моделирования существенно шире. В зависимо­сти от этапа и назначения проводимых исследований применяется один из трех наиболее распространенных видов имитационных экспериментов:

исследование относительного влияния различных факторов на значения вы­ходных характеристик системы;

нахождение аналитической зависимости между интересующими исследователя выходными характеристиками и факторами;

отыскание оптимальных значений параметров системы (так называемый «экстремальный эксперимент»).

Вид эксперимента влияет не только на выбор схемы ее формализации, но также на построение плана эксперимента и выбор метода обработки его результатов.

С точки зрения организации взаимодействия исследователя с моделью в ходе эксперимента ИМ делятся на автоматические и диалоговые.

 

Автоматическими называются ИМ, взаимодействие пользователя с которы­ми сводится только к вводу исходной информации и управлению началом и окон­чанием работы моделей.

 

Диалоговыми называются ИМ, позволяющие исследователю активно управ­лять ходом моделирования.

 

Тактическое планирование

 

Имитационное моделирование не ограничи­вается разработкой модели и написанием машинной программы; моделирование представляет собой статистический эксперимент, и его результаты необходимо рассматривать именно с этой точки зре­ния. В частности, для любого эксперимента, связанного с модели­рованием, необходимо ответить на следующие вопросы:

Какова должна быть продолжительность прогона для дости­жения стационарных условий?

Каким образом  получать статистически независимые наблю­дения?

Каким образом можно получать результаты моделирования, оставляя затраты на разумном уровне и не слишком жертвуя точ­ностью?

Сколько наблюдений требуется для достижения необходимого значения доверительных интервалов?

Тактическое планирование связано с решением следующих проблем:

определение начальных условий и их влияние достижение результата;

обеспечение точности и достоверности результатов;

уменьшение дисперсии оценок характеристик изучаемой системы;

выбор правила автоматической остановки имитационного эксперимента.

 

1. Проблема определения начального условия

 

Эта проблема возникает из-за того, что у имитационной после запуска существует переходный период пока разыгрываемые случайные  процессы не выйдут на установившийся режим. Используют следующие способы решения этой проблемы:

Увеличивают длительность прогона так, чтобы влияние переходного периода было незначительным.

Предварительно «раскручивают процессы имитации случайных величин».

Искусственно подбирают начальные условия близкие к естественным режимам.

 

2. Проблема обеспечения точности и достоверности

 

Обработка результатов имитационного эксперимента принципиально не может дать точных значений оцениваемых величин из-за  стохастичности  и конечного числа реализаций.

Таким образом если существует некоторая функция эффективности системы E, то  ,        - оценка функции эффективности системы. Введём определения:

 - абсолютная погрешность

     -  относительная погрешность

 - достоверность оценки,  - нормативное значение.

Пусть целью машинного эксперимента будет получение оценки вероятности некоторого события А,  P=P(A). В качестве такой оценки обычно выбирается частость . Здесь m- число положительных исходов,                    N- общее число исходов. В силу центральной предельной теоремы частость при   является случайной величиной, имеющей нормальное распределение с математическим ожиданием    и дисперсией   . Поэтому для оценки достоверности можно воспользоваться следующем соотношениями:

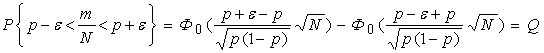
Учитывая, что для функций Лапласа. получим 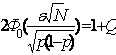. Тогда  - квантиль нормального распределения порядка . В результате абсолютная погрешность определяется как , т.е. абсолютная погрешность  обратно пропорциональна  . Можно вычислить количество реализаций модели необходимых для получения оценки  с погрешностью  и достоверностью Q.

В практических случаях для того чтобы оценить вероятность    целесообразно число прогонов модели выбирать . Очевидно что даже для простых систем метод статистического моделирования приводит к большим затратам машинного времени.

Часто в качестве функции эффективности систем используется среднее значение некоторой случайной величины. Пусть  имеет математическое ожидание  a  и дисперсию . В качестве оценки a используется среднее арифметическое.

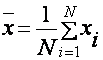
В силу центральной предельной теоремы при   среднее арифметическое является случайной величиной, подчиняющееся нормальному распределению . Для математического ожидания a, абсолютная погрешность найденная из уравнения для квантиля    , а количество реализаций  или .

Пусть в качестве эффективности системы используется дисперсия некоторой случайной величины , а  - оценка дисперсии по выборке объема N. Математическое ожидание и дисперсия этой оценки:

               ,

где - центральный момент 4-го порядка.

Абсолютная ошибка дисперсии  , а число реализаций

Для случая, когда величина распределена по нормальному закону            

Исходя из этих формул можно сделать вывод, что выгодно выбирать такие оцениваемые показатели эффективности систем, которые имеют малые дисперсии.

Вопрос 27. Методы понижения дисперсии.

 

 

3. Проблема уменьшения дисперсий оценок характеристик процесса функционирования моделируемых систем

3. Проблема уменьшения дисперсий оценок характеристик процесса функционирования моделируемых систем

 

Располагая набором преобразований случайной величины, сохраняющих её математическое ожидание, но изменяющих дисперсию, можно строить модификации метода Монте-Карло более эффективные, чем исходная. Рассмотрим такие преобразования применительно к задаче вычисления интеграла.

 

1. Метод выделения главной части

 

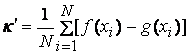Пусть требуется вычислить интеграл  и имеется достаточно близкая к f(x) функция  g(x) такая, что интеграл   Может быть вычислен аналитически или с помощью простой квадратурной формулы. Тогда    и  достаточно оценить интеграл  методом Монте-Карло с помощью суммы  , где xi независимы и распределены по закону .

Если обозначить   то

 - оценивается аналитически или по выборке умеренного объёма.

 

2. Метод существенной выборки

 

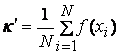Пусть интеграл  оценивается с помощью суммы  , где xi  – независимые случайные величины с распределением вероятностей . В этом случае . Пусть  – произвольная вероятностная мера такая, что - абсолютно непрерывна по отношению к ней. Тогда  и может быть использована оценка 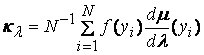, где yi распределены по закону .

Дисперсия 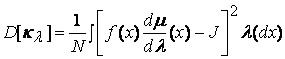.  Таким образом, получено семейство несмещённых оценок для интеграла J1, зависящих от меры .

 

Если f(x) неотрицательная функция то можно выбрать  такую, что имеет минимальную дисперсию.

В настоящее время существуют методы, позволяющие при заданном числе реализаций увеличить точность оценок. Эти методы, как правило, используют априорную информацию о структуре и поведении системы. Часть из них основана на специальном построении моделирующего алгоритма, позволяющего получить положительную корреляцию за счет управления генерацией случайных величин.

Пусть, например, производится сравнение двух вариантов некоторой системы  по средним значениям некоторых критериев - оценка критерия варианта 1; - оценка критерия варианта 2, имеющих дисперсии ,  

и коэффициент корреляции . Дисперсию погрешности оценки  можно найти из соотношения

,

где , .

Из этой формулы видно, что если R=0 , то мы имеем независимые испытания и

, для зависимых испытаний R>0 и .

Положительные значения коэффициента корреляции можно получить, когда в имитационных экспериментах используются одни и те же псевдослучайные последовательности. Такой подход однако может существенно исказить физическую интерпретацию изучаемого явления. В общем случае приемы понижения дисперсии оценок подбираются индивидуально для каждой задачи.

 

4.. Проблема выбора правил автоматической остановки

 

Обычно задают требуемое количество реализаций или длины интервала моделирования. Другой способ задание доверительных интервалов оцениваемых величин и остановка прогона машинной модели по достижению этих интервалов. Наиболее эффективным способом в настоящее время является способ последовательного анализа. В последовательном анализе объем выборки не фиксируется, а после каждого i-го  наблюдения принимается одно из следующих решений:

Принять данную гипотезу

Отвергнуть гипотезу

Продолжить испытания

Благодаря такому подходу объем выборки может быть уменьшен.

Пусть распределение генеральной совокупности характеризуется функцией плотности вероятности . Задача состоит в оценке неизвестного параметра  . Определим нулевую и альтернативную гипотезы

                 .

Гипотезы  проверяют на основании выборки нарастающего объёма m. Вероятность получения выборки  при условии, что  - верна

Вероятность получения выборки  при условии, что  - верна

.

            Процедура проверки строится на отношении правдоподобия:

 

,

где ;       ;             - ошибка первого рода – гипотеза верна, но отвергается;    - ошибка второго рода – гипотеза неверна, но принимается.

Вопрос 28. Оценка качества имитационной модели.

 

Оценка качества имитационной модели

 

Оценка качества модели является завершающим этапом ее разработки и пре­следует две цели:

проверить соответствие модели ее предназначению (целям исследования);

оценить достоверность и статистические характеристики результатов, полу­чаемых при проведении модельных экспериментов.

При аналитическом моделировании достоверность результатов определяется двумя основными факторами:            |

1) корректным выбором математического аппарата, используемого для описания исследуемой системы;           

2) методической ошибкой, присущей данному математическому методу.

При имитационном моделировании на достоверность результатов влияет целый ряд дополнительных факторов, основными из которых являются:

моделирование случайных факторов, основанное на использовании датчиков случайных чисел, которые могут вносить «искажения» в поведение модели;

наличие нестационарного режима работы модели;

использование нескольких разнотипных математических методов в рамках одной модели;

зависимость результатов моделирования от плана эксперимента;

необходимость синхронизации работы отдельных компонентов модели;

наличие модели рабочей нагрузки, качество которой зависит, в свою очередь, от тех же факторов.

Пригодность имитационной модели для решения задач исследования характе­ризуется тем, в какой степени она обладает так называемыми целевыми свойства­ми. Основными из них являются:

 

адекватность;

устойчивость;

чувствительность.

 

Оценка адекватности модели. В общем случае под адекватностью понимают степень соответствия модели тому реальному явлению или объекту, для описания которого она строится.

Процедура оценки основана на сравнении измерений на реальной системе и результатов экспериментов на модели и может проводиться различными способа­ми. Наиболее распространенные из них:

по средним значениям откликов модели и системы;

по дисперсиям отклонений откликов модели от среднего значения откликов системы;

по максимальному значению относительных отклонений откликов модели от откликов системы.

     Названные способы оценки достаточно близки между собой по сути, поэтому ограничимся рассмотрением первого из них.

При этом способе проверяется гипотеза о близости среднего значения наблюда­емой переменной Y среднему значению отклика реальной системы Y*. В результате No опытов на реальной системе получают множество значений (вы­борку) Y*. Выполнив Nm экспериментов на модели, также получают множество значений наблюдаемой переменной Y. Затем вычисляются оценки математического ожидания и дисперсии откликов модели и системы, после чего выдвигается гипотеза о близости средних значений величин Y* и Y (в статистическом смысле). Основой для проверки гипотезы явля­ется t-статистика (распределение Стьюдента), Ее значение, вычисленное по резуль­татам испытаний, сравнивается с критическим значением tкр, взятым из справоч­ной таблицы. Если выполняется неравенство t < tкр, то гипотеза принимается.

На проектируемой системе провести измерения, естественно, не представляется возмож­ным. Единственный способ преодолеть это препятствие заключается в том, чтобы принять в качестве эталонного объекта концептуальную модель проектируемой сис­темы. Тогда оценка адекватности программно реализованной модели заключается в проверке того, насколько корректно она отражает концептуальную модель. Данная проблема сходна с проверкой корректности любой компьютерной программы, и ее можно решать соответствующими методами, например с помощью тестирования.

 

Оценка устойчивости модели. При оценке адекватности модели как существу­ющей, так и проектируемой системе реально может быть использовано лишь огра­ниченное подмножество всех возможных значений входных параметров (рабочей нагрузки и внешней среды). В связи с этим для обоснования достоверности полу­чаемых результатов моделирования большое значение имеет проверка устойчиво­сти модели. В теории моделирования это понятие трактуется следующим образом.

Устойчивость модели — это ее способность сохранять адекватность при иссле­довании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы.

Универсальной процеду­ры проверки устойчивости модели не существует. Разработчик вынужден прибегать к методам «для данного случая», частичным тестам и здравому смыслу. Часто бывает, по­лезна апостериорная проверка. Она состоит в сравнении результатов моделирования и результатов измерений на системе после внесения в нее изменений. Если результаты моделирования приемлемы, уверенность в устойчивости модели возрастает.

В общем случае можно утверждать, что чем ближе структура модели структуре системы и чем выше степень детализации, тем устойчивее модель.

Устойчивость результатов моделирования может быть также оценена методами математической статистики. Здесь уместно вспомнить основную задачу математи­ческой статистики. Она заключается в том, чтобы проверить гипотезу относительно свойств некоторого множества элементов, называемого генеральной совокуп­ностью, оценивая свойства какого-либо подмножества генеральной совокупности (т.е. выборки). В генеральной совокупности исследователя обычно интересует не­который признак, который обусловлен случайностью и может иметь качественный или количественный характер. В данном случае именно устойчивость результатов моделирования можно рас­сматривать как признак, подлежащий оценке. Для проверки гипотезы об устойчи­вости результатов может быть использован критерий Уилкоксона.

Критерий Уилкоксона служит для проверки того, относятся ли две выборки к од­ной и той же генеральной совокупности (т. е. обладают ли они одним и тем же статис­тическим признаком). Например, в двух партиях некоторой продукции измеряется определенный признак, и требуется проверить гипотезу о том, что этот признак имеет в обеих партиях одинаковое распределение; другими словами, необходимо убедиться, что технологический процесс от партии к партии изменяется несущественно.

При статистической оценке устойчивости модели соответствующая гипотеза может быть сформулирована следующим образом: при изменении входной (рабо­чей) нагрузки или структуры ИМ закон распределения результатов моделирова­ния остается неизменным.

Проверку указанной гипотезы Н проводят в следующем порядке:

формируют две выборки X=(x1 ..., хn) и Y= (y1 ..., уm), полученные для различных значений рабочей нагрузки;

относительно законов распределения X и Y никаких предположений не делается;

значения обеих выборок упорядочиваются вместе по возрастанию;

ана­лизируется взаимное расположение xi и yi (в случае yi < xi говорят, что пара значе­ний (xi , yi) образует инверсию);

подсчитывают полное число инверсий U.

Если гипотеза верна, то U не должно сильно отклоняться от своего математического ожидания М:   .

От гипотезы отказываются, если   , ( определяют по таблице для заданного уровня значимости).

 

Оценка чувствительности ИМ. Очевидно, что устойчивость является положитель­ным свойством модели. Однако если изменение входных воздействий или параметров модели (в некотором заданном диапазоне) не отражается на значениях выходных пара­метров, то польза от такой модели невелика (ее можно назвать «бесчувственной»). В связи с этим возникает задача оценивания чувствительности модели к изменению пара­метров рабочей нагрузки и внутренних параметров самой системы.

Такую оценку проводят по каждому параметру Xk в отдельности. Основана она на том, что обычно диапазон возможных изменений параметра известен. Одна из наиболее простых и распространенных процедур оценивания состоит в следующем.

Вычисляется величина относительного среднего приращения параметра Xk:

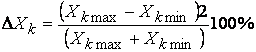
В точках проводится пара модельных экспериментов Y1, Y2  при средних фиксированных значениях остальных параметров.

вычисляется относительное приращение наблюдаемой переменной Y:

В результате для k-ro параметра модели имеют пару значении (,), харак­теризующую чувствительность модели по этому параметру.

Аналогично формируются пары для остальных параметров модели, которые образуют множество {,}. Данные, полученные при оценке чувствительности модели, могут быть ис­пользованы, в частности, при планировании экспериментов: большее внима­ние должно уделяться тем параметрам, по которым модель является более чув­ствительной.

 

Калибровка модели. Если в результате проведенной оценки качества модели оказалось, что ее целевые свойства не удовлетворяют разработчика, необходимо выполнить ее калибровку, т. е. коррекцию с целью приведения в соответствие предъявляемым требованиям.

Как правило, процесс калибровки носит итеративный характер и состоит из трех основных этапов:

глобальные изменения модели (например, введение новых процессов, изме-­
нение типов событий и т. д.);

локальные изменения (в частности, изменение некоторых законов распреде-­
ления моделируемых случайных величин);

изменение специальных параметров, называемых калибровочными.

Целесообразно объединить оценку целевых свойств ИМ и ее калибров­ку в единый процесс.

Процедура калибровки состоит из трех шагов, каждый из которых является ите­ративным.

 

Рис. 4.3.  Схема процесса калибровки ИМ

 

Шаг 1. Сравнение выходных распределений.

Цель − оценка адекватности ИМ. Критерии сравнения могут быть различны. В частности, может использоваться величина разности между средними значениями откликов модели и системы. Устранение различий на этом шаге основано на внесении глобальных изменений.

 

Шаг 2. Балансировка модели.

Основная задача − оценка устойчивости и чувствительности модели. По его резуль­татам, как правило, производятся локальные изменения (но возможны и глобальные).

 

Шаг 3. Оптимизация модели.

Цель этого этапа − обеспечение требуемой точности результатов. Здесь возмож­ны три основных направления работ:

дополнительная проверка качества датчиков СЧ;

снижение влияния переходного режима;

применение специальных методов понижения дисперсии.