Тема 4. Имитационное моделирование.

Вопрос 23. Имитационные модели. Математическая платформа и принципы разработки.

Тема 4. Имитационное моделирование.

Имитационная модель – это формальное описание логики функционирования системы, учитывающее наиболее существенные причинно следственные связи и обеспечивающее проведение статистических экспериментов.

Статистический эксперимент – это эксперимент, проводимый с помощью аналитической модели, позволяющий учесть влияние всех входных воздействий, часть из которых носит случайный характер. В результате статистического эксперимента получается набор данных, на которых как на выборках оценивается среднее значение и стандартное отклонение параметра изучаемой системы.

Вычислительной платформой имитационного моделирования является метод Монте-Карло, состоящий в том, что результаты испытания зависят от значений случайной величины, распределённой по заданному закону.

Теоретической основой имитационного моделирования являются предельные теоремы теории вероятностей (теоремы Чебышева, Бернулли, Пуассона).

Теорема П. Л. Чебышева

Если дисперсии независимых случайных величин ограничены, то при увеличении числа испытаний арифметическое среднее этих величин сходится по вероятности к арифметическому среднему их математических ожиданий.

Теорема Я. Бернули

Последовательность относительных частот появления события в независимых повторных испытаниях сходится по вероятности к вероятности появления события в каждом испытании.

Теорема Пуассона

Если вероятность события в некотором испытании не меняется, когда становятся известными результаты предыдущих испытаний, то с ростом числа испытаний частотность события сходится по вероятности к средней арифметической вероятностей этого события.

Справедливы следующие выводы для любого имитационного эксперимента независимо от физической природы и типа моделируемой системы:

Каждый прогон модели рассматривается как одно наблюдение (реализация);
С увеличением продолжительности прогона (объёма испытаний) отклонения оцениваемой величины от её точного значения уменьшается;
Влияние переходных условий можно уменьшить, если увеличить количество прогонов;
Существует предел для числа М (M - объём испытаний), за которым модель уже не даёт существенного повышения точности результата.

Вопрос 24. Метод Монте-Карло на примере вычисления площади плоских фигур.

Пример:

Пусть требуется определить площадь круга известного диаметра с помощью выборок из значений случайной величины. Впишем круг в квадрат; таким образом, стороны квадрата будут равны диаметру круга. Разобьем далее квадрат на единичные квадраты (каждый площадью 1). Разумеется, можно найти площадь круга подсчетом числа единичных квадратов (или их частей), попавших внутрь круга. Однако в методе Монте-Карло это достигается использованием выборок.

Пусть круг имеет радиус r=5 см и его центр в точке (1, 2) . Уравнение окружности будет иметь вид:

На рисунке 4.1 изображены круг и описанный около него квадрат. Квадрат определяется его вершинами (—4, —3), (6, —3), (—4, 7) и (6, 7), которые получаются непосредственно из геометрических свойств фигуры. Любая точка (х, у) внутри квадрата или на его границе должна удовлетворять неравенствам —4<х<6 и —3< у<7.

Рис. 4.1 Рассчётная схема – вычисление площади круга методом Монте-Карло.

Применение выборок при использовании метода Монте-Карло основано на предположении, что все точки в квадрате могут появляться с одинаковой вероятностью, т. е. х и у распределены равномерно с плотностью

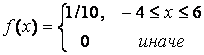
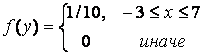
Определим теперь точку (х, у) в соответствии с распределениями f(x)и f(y). Продолжая этот процесс, подсчитаем число точек, попавших внутрь круга или на окружность. Предположим, что выборка состоит из п наблюдений иm точек попали внутрь круга или на окружность. Тогда Оценка площади круга:

т/п* (площадь квадрата) = (т/п)(10х10) = 100 т/п.

Подобный способ оценивания площади круга можно обосновать тем, что в процессе получения выборки любая точка (х,у) может с одинаковой вероятностью попасть в любое место квадрата. Поэтому отношение т/п представляет оценку площади круга относительно площади квадрата.

Можно сделать следующие заключения:

1. С ростом числа генерируемых точек (т. е. продолжительности прогона модели) оценки площади круга приближаются к точному значению (78,54 см2). Это условие обычно достигается после повторения эксперимента достаточное количество раз. Наблюдаемое явление типично для результатов любой имитационной модели. Обычно в большинстве имитационных моделей нас интересуют результаты, полученные в стационарных условиях.

2. Прогоны модели (отличающихся друг от друга только последовательностью используемых случайных чисел) дают различные оценки при одном и том же значении п. Каждый прогон можно рассматривать как наблюдение в эксперименте, связанном с моделированием.

3. Влияние переходных условий уменьшается, если усреднить результаты серий. Существует предел, за которым увеличение продолжительности прогона модели уже не дает существенного повышения точности результата, измеряемого дисперсией. Это замечание представляется чрезвычайно важным, поскольку затраты на эксплуатацию имитационной модели прямо пропорциональны продолжительности прогонов. Поэтому желательно найти компромисс между большой точностью (т. е. малой дисперсией) и небольшими затратами на процедуру получения результатов.

4. Ввиду того, что оценки площади имеют разброс, важно, чтобы результаты эксперимента, связанного с моделированием, были выражены в виде доверительных интервалов, показывающих величину отклонения от точного значения.

Вопрос 25. Моделирование случайных величин с заданным законом распределения.

Моделирование случайных величин с заданным законом распределения

Имитационное моделирование опирается на процедуры генерации случайных чисел с заданными законами распределения. Для большинства известных законов в современных математических пакетах имеются соответствующие генераторы. Все эти генераторы, а также создаваемые пользователем используют в качестве базового алгоритм датчика стандартной равномерно распределённой случайной величины, закон распределения которой

;

Наиболее распространённым является следующий алгоритм . Здесь , символ {…} означает операцию отбрасывания целой части с оставлением дробной части в десятичной форме, , m – количество разрядов двоичного представления чисел в ЭВМ.

Формируемая последовательность является псевдослучайной в том смысле, что при фиксированном получается одинаковая последовательность чисел , причём через L обращений к датчику значения начинают повторяться. Величина называется периодом последовательности для , M.

Имея датчик равномерной случайной величины в интервале [0,1], могут быть получены простые алгоритмы с другими параметрами и распределениями.

Метод нелинейного функционального преобразования.

ТЕОРЕМА: Пусть случайная величина имеет равномерное распределение в интервале [0,1] и связана со случайной величиной соотношением ,

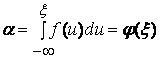где f(u) - некоторая функция, удовлетворяющая соотношениям .

Тогда имеет плотность распределения вероятностей вида f(u) и может быть найдена на основе обратного функционального преобразования

Пример.

Пусть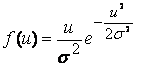 - закон Релея.

Тогда

Метод исключений (Фон-Неймана)

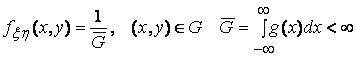ТЕОРЕМА: Пусть функция и на её основе определено множество значений вещественных переменных . Пусть также совместная плотность распределения случайных величин и на множестве G равна , т.е. имеет равномерный вид. Тогда плотность распределения вероятностей случайной величины равна .

Для получения алгоритма моделирования на основе этой теоремы используются следующие построения. Пусть имеется способ моделирования совместно равновероятных случайных величин в области накрывающую требуемую область G:

Тогда для генерации случайной величины с законом распределения требуется выполнить последовательность действий:

Генерируется по равномерному закону в пределах случайная точка с координатами см. рис. 1.

Если , то полученная точка исключается из рассмотрения и осуществляется возврат на первый шаг.

Если , то используется в качестве очередного значения искомой случайной величины.

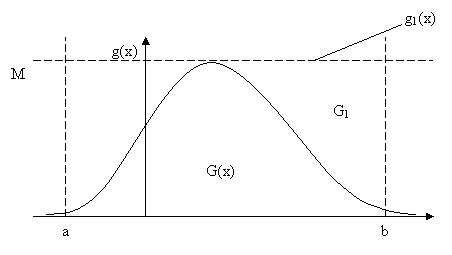
Рис.1 Генерация случайных точек