Вопрос 20. Модели в пространстве состояний.

3.3 Метод пространства состояний

Анализ и синтез технических систем обычно осуществляется одним из двух основных методов:

Первый метод основан на преобразовании Лапласа, Z – преобразований, переходных функций, структурных схем и графов.

Второй - метод пространства состояний.

Перед традиционным методом (частотным) он имеет следующие преимущества:

описание в пространстве состояний удобно для решения задач на ЭВМ.

позволяет унифицировать описание одномерных и многомерных систем.

может применяться к нелинейным и нестационарным системам.

Схема получения решения ОДУ при моделировании систем следующая:

1. Конструируется эквивалентная передаточная функция, сводящая структурную схему объекта к виду:

2. По передаточной функции 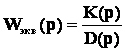находится выражение для переходной функции из формулы Хевисайта:

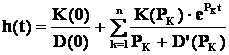
- корни характеристического уравнения .

3. Вычисление импульсной характеристики объекта .

4. Решение ОДУ (выходной сигнал) представляется в виде: .

Понятие состояния в технических науках определяется аксиоматически, т.е. перечислением совокупности присущих ему свойств.

Состояние системы – это некоторый параметр позволяющий сделать однозначным определение её выхода по входу. Состояние должно удовлетворять следующим аксиомам совместности:

А-1: Выход у(t) для всех определяется однозначно, если заданы и .

А-2: Если траекторию системы разбить на ряд участков, то движение на каждом из них можно рассматривать как новую траекторию при соответствующем начальном состоянии.

Состояние динамической системы должно изменяться, в зависимости от входного процесса и начального состояния.

Множество возможных значений состояния системы называется пространством состояний. Если рассматривается линейное пространство , тогда x(t) есть n – мерный вещественный вектор.

Состояние определяется неединственным образом, а с точностью до взаимно однозначного преобразования , , которых может быть сколь угодно много. В частности, если , а Т – некоторая невырожденная матрица порядка n (detT≠0), то вектор . Такой переход называется преобразование базиса в пространстве состояний. Это преобразование не нарушает входных – выходных соотношений в описании системы.

Для конечномерных непрерывных систем уравнения состояния могут быть представлены в виде:

, , – уравнение состояния (эволюционное);

– уравнение выхода;

, , , , – вектор функции.

Если , линейны по х, u то уравнения состояния могут быть записаны в виде:

, ,

, , , .

Уравнения состояния иллюстрируются структурной схемой:

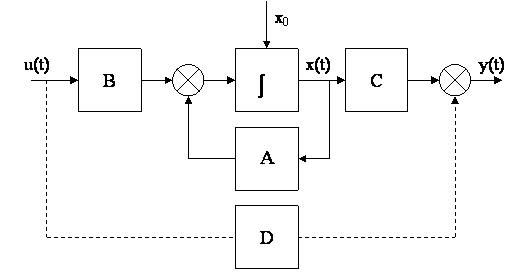
Если , то система называется собственной. Если A, B, C, D не завися от времени, то система называется стационарной. Для стационарных систем можно считать .

Вопрос 21. Линеаризация уравнений состояния.

Линеаризация уравнений состояния.

Пусть динамика системы описывается уравнениями состояния: . Введем (“опорные”) функции . Найдем линейную часть разложения функций , в окрестности x*, u* в ряд Тейлора. В результате получим:

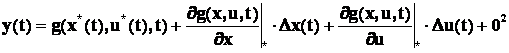
Здесь – отклонение состояния исходной модели по отношению к вектору ; – отклонение входного процесса от .

Матрицы Якоби: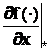, , 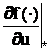, 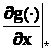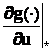– матрицы частных производных вектор-функций по компонентам векторов x, u.

Из этих уравнений следует общий вид уравнений для приращений:

Конкретный вид линеаризованной модели зависит от выбора опорных функций , .

Уравнения состояния при соединении систем

Системы, состоящие из соединенных между собой подсистем называют “композитными”. Описание моделей таких систем уравнениями состояния опирается на специальную форму матричных уравнений.

Пусть композитная система состоит из двух независимых подсистем.

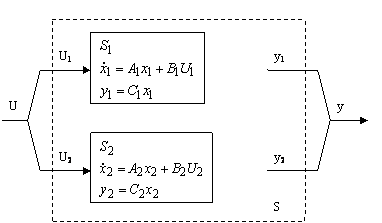
Входом системы является вектор, полученный объединением входов каждой подсистемы, а выходом – объединение их выходов.

, ; ; ; , , . Введем совокупные (общие) векторы:

состояния ;

входа ;

выхода .

Тогда можно объединить уравнения в одно , , в котором матрицы , , имеют следующую блочную структуру:

, , .

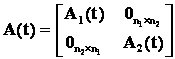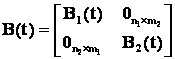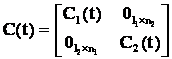Рассмотрим последовательное соединение.

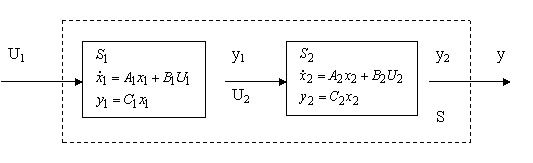
, , , при этом совпадают размерности . С учетом связи уравнения подсистем имеют вид:

, ;

, .

Матрицы уравнений , имеют вид:

, , .

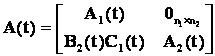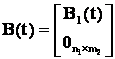Соединение с обратной связью.

, , , , .

, .

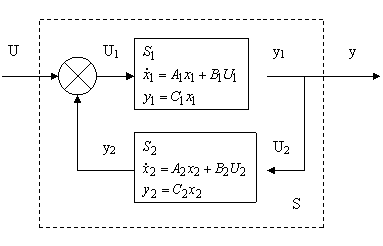
С учетом связи между подсистемами их уравнения принимают вид:

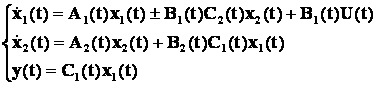
Матрицы в уравнениях стандартного вида определяются выражениями:

, , .

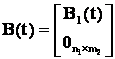Фазовые траектории и фазовые портреты линейных систем.

Рассмотрим собственные движения системы, (входное воздействие отсутствует, система автономна и стационарна).

Каждому решению этой системы ставится в соответствие движение точки по некоторой кривой в пространстве состояний фазовая траектория. Это дает возможность получить кинематическую интерпретацию поведения систем. Фазовым портретом системы называется совокупность фазовых траекторий, полученных при различных начальных условиях.

Из условий существования и единственности решения системы уравнений следуют основные свойства фазовых траекторий:

1. Через каждую точку пространства состояний проходит некоторая фазовая траектория. (Фазовый портрет системы может быть заполнен фазовыми траекториями сколь угодно плотно.)

2. Никакая фазовая траектория не имеет точек разветвления.

3. Никакие различные траектории не могут иметь точек пересечения. (Траектории либо не пересекаются, либо совпадают.)

4. Самопересекающиеся траектории соответствуют либо состояниям равновесия , либо периодическим движениям , но при хотя бы для одной компоненты выполнено .

Фазовая траектория периодического процесса представляет собой замкнутую кривую, называемую замкнутой траекторией, орбитой или циклом.

Пусть в момент времени точка проходит состояние . Значение называют фазовой скоростью. Оно зависит от координат точки, через которую в данный момент проходит траектория. Для автономных линейных систем вектор фазовой скорости в точке определяется равенством . Направление совпадает с направлением касательной к фазовой траектории, а модуль характеризует темп движения точки вдоль траектории. Если в каждой точке фазового пространства изобразить соответствующую ей фазовую скорость, то получим поле фазовых скоростей. Для такого построения не надо решать дифференциальное уравнение. Поле фазовых скоростей дает наглядное представление о поведении системы.

Вопрос 22. Передаточная функция линейной системы.

3.3. Передаточная функция линейной системы

Для линейных систем передаточные функции могут быть определены по уравнениям состояния. Рассмотрим линейную стационарную систему непрерывного времени

либо дискретную стационарную систему

где

Определение

Выражение называется передаточной функцией системы (* *) от входа u к выходу y.

Здесь является матричной функцией размера от комплексного аргумента.

Для строго реализуемых систем передаточная функция имеет более простой вид

Размер матрицы определяется размерностями входа и выхода системы. для систем с одним входом и одним выходом становится отношением многочленов от . В общем случае получается матрица, элементами которой являются передаточные функции , от каждого входа к каждому выходу :

Наибольшую сложность в вычислительном процессе получения представляет вычисление резольвенты матрицы . По правилу обращения матриц

где через обозначена матрица алгебраических дополнений к , или присоединённая (к ) матрица. Знаменатель этого выражения есть скалярный многочлен степени n, .

Он называется характеристическим многочленом матрицы . Таким образом, все передаточные функции вычисленные по формуле (**), имеют одинаковые знаменатели . Поэтому характеристический многочлен матрицы совпадает со знаменателем передаточной функции системы. Вид переходного процесса в системе, её устойчивость определяются корнями данного многочлена. Значения называются собственными числами матрицы . Множество собственных чисел известно как спектр данной матрицы.

Для вычисления резольвенты на ЭВМ разработаны ряд специальных алгоритмов. При «ручном» вычислении передаточной функции оказывается более удобной запись уравнений состояния в операторной форме. Выходная переменная определяется через решение систем линейных алгебраических уравнений.

При построении линейной математической модели объекта осуществляется, как правило, следующая последовательность действий:

Составляется принципиальная схема, отражающая структуру соединения элементов объекта, выделяются каналы управления и помех. На основе технологического процесса определяются режимные характеристики всех элементов объекта.

Формулирование допущений об определяющих физических процессах, сосредоточенности или распределённости параметров объекта.

Запись необходимых уравнений для определяющих физических процессов.

Линеаризация исходных дифференциальных уравнений.

Алгебраические преобразования линеаризованных уравнений к передаточной функции по искомому каналу с получением выражений для коэффициентов.

Производные в левой и правой частях уравнения заменяются на s в степени, равной порядку заменяемой производной;

Полученный полином правой части есть числитель передаточной функции, а полином левой части – её знаменатель.

Вычисление численных значений коэффициентов передаточной функции и анализ её структуры.

Метод передаточных функций реализован во многих пакетах моделирования. Он удобен тем, что позволяет представлять функциональные структуры при визуальном программировании. Например в пакете LabVIEW моделирование включает инструменты, изучающие динамику систем, описанных линейными, неизменяющимися во времени, непрерывными(LTI) и дискретными моделями. С их помощью можно создавать детерминированные модели пространства состояний, передаточные функции и полюсно-нулевое представление (zero-pole-gain models). Эти формы можно использовать для описания одномерных (SISO) и многомерных (MIMO) систем.

Deterministic State-Space Model

(Детерминированная Модель Пространства Состояний)

Непрерывная

x(t)=Ax(t)+Bu(t)

y(t)=Cx(t)+Du(t)

Дискретная

x(k+1)=Ax(k)+Bu(k) k – дискрет времени (шаг квантования)

y(k)=Cx(k)+Du(k)

Stochastic State-Space Model

(Стохастическая Модель Пространства Состояний)

Непрерывная

x(t)=Ax(t)+Bu(t)+Gw(t) – зашумление вектора состояния

y(t)=Cx(t)+Du(t)+Hw(t)+v(t) – помехи при измерениях

Дискретная

x(k+1)=Ax(k)+Bu(k)+Gw(k)

y(k)=Cx(k)+Du(k)+Hw(k)+v(k)

Second-Order Statistics Noise Model

Q = E{w . wT} – E{w} . ET{w}
R = E{v . vT} – E{v} . ET{v}
N = E{w . vT} – E{w} . ET{v}

где,

n – это число состояний модели,

m – это количество входов системы,

r – это количество выходов системы,

t – время,

k – шаг квантования по времени умноженный на дискретный шаг времени, где дискретный шаг равен 0,1,2..

x – вектор состояния,

u – вектор входа,

y – вектор выхода,

w – процесс зашумления вектора,

v – вектор помех измерения,

A – это матрица n*n состояний данной модели,

B – это матрица n*m входов данной модели,

C – это матрица r*n выходов данной модели,

D – это матрица r*m прямой передачи данной модели,

G – это матричное соотношение w к состояниям системы,

H – это матричное соотношение w к выходам системы,

Q – это автоковариационная матрица w,

R - это автоковариационная матрица v,

N – это матрица взаимной ковариации между w и v,

E{} - обозначает ожидаемое значение или среднее значение выбранных параметров.

Transfer Function Model

(Модель Передаточной Функции)

Непрерывная SISO MIMO

Дискретная

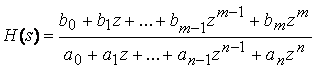
Zero-Pole-Gain Model

Непрерывная SISO MIMO

Дискретная

Где s –значение преобразований Лапласа и непрерывное время,

z - это дискретное время,

m – это порядок числителя функции полинома,

n – порядок знаменателя функции полинома,

bm – это коэффициенты числителя функции полинома,

an - это коэффициенты знаменателя функции полинома,

Zm – это число нулей модели,

Pn – это число полюсов модели,

k – коэффициент усиления модели,

Hij – это передаточная функция или zero-pole-gain эквивалент ith входов и jth выходов MIMO модели.

Пример

Существование в реальных физических системах неустановившихся динамических режимов обусловлено наличием аккумуляторов информации, вещества или энергии изменение количества, которых не может произойти мгновенно. В зависимости от вида этих аккумуляторов (ёмкостей) динамические системы делятся на системы: с сосредоточенными ёмкостями (в которых определены границы между ними и можно указать их число) и с распределёнными ёмкостями.

Рассматривается одна ёмкость – бак, в который непрерывно поступает и из которого уходит жидкость; количество аккумулированной в баке жидкости определяется значением её уровня.

Если плотность жидкости не меняется, то уравнение материального баланса в течение некоторого небольшого интервала времени будет иметь вид:

При получим уравнение материального баланса при непрерывно меняющихся расходах жидкости на притоке и стоке:

где F - площадь сечения бака.

Расход жидкости на притоке и стоке является функцией перепада давления на клапанах и степени их открытия. Упрощённо эти функции можно представить в виде:

где , соответственно давление на притоке перед клапаном и на стоке после клапана, которые будем полагать постоянными, измеряемыми в единицах водяного столба; и - постоянные коэффициенты.

Уравнение состояния (нелинейное) и уравнение для выходной (контролируемой) величины – уравнение связи получаем в следующем виде:

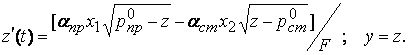
Соответствующее линеаризованное уравнение определится следующим образом:

а его коэффициенты

;

Установившиеся значения должны удовлетворять уравнению равновесного режима

Примем

Отсчёт переменных в этих уравнениях следует проводить от равновесных значений. Исключением эта система приводится к уравнению, связывающему выходную и входную величины:

Найдём решение для случая, когда входное воздействие x1 при t=0 меняется скачком на величину x0, при условии, что до этого объект находился в покое. Соответствующая передаточная функция определяется формулой

Изображение входного воздействия X(s)=x0/s, а изображение выходной величины . Решение, полученное обратным преобразованием Лапласа имеет вид:

Обратным преобразованием Лапласа передаточной функции можно получить импульсную переходную характеристику:

Теперь можно получить отклик на произвольное воздействие, например

Отклик содержит переходную и установившуюся составляющие, причем у установившегося сигнала та же частота что и у воздействия.

Таким образом, завершено исследование модели одноёмкостного накопителя. Подобный анализ пригоден только для исследования линейных, устойчивых систем.

Достаточно универсальным методом исследования нелинейных, нестационарных и неустойчивых систем является имитационное моделирование. В этом разделе под имитационным моделированием понимается рекуррентный вычислительный процесс, осуществляющий пошаговое решение дифференциального уравнения записанного в разностной форме. Так для одноёмкостного накопителя разностное уравнение имеет вид:

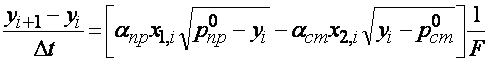Здесь - интервал квантования.

Из этого уравнения получается формула, которая позволяет вычислять очередное дискретное значение yi+1 по её предыдущему значению yi и предыдущим дискретным значениям входных воздействий x1,i, x2,i , начиная с i=0: