Тема 3. Моделирование технических систем

Вопрос 17. Функциональное моделирование.

Модель – представление существенных аспектов системы, обеспечивающее в удобной форме знания об этой системе. Выделяют следующие области применения:

Интерпретация прошлого поведения и обобщение имеющихся знаний;

Предсказание будущего поведения, определение тенденций;

Оценивание неизмеряемых величин и диагностические измерения.

Получение знаний о процессе или системе, для автоматического управления ими.

Определение.

Отыскание по входным и выходным сигналам некоторой системы адекватной ей математической модели из заданного класса называется идентификацией.

Ниже приведена схема идентификации.

3.1. Функциональное моделирование

Пусть на входе объекта измеряются значения вектора входных переменных , распределённые с неизвестной плотностью, а на выходе – соответствующие значения выходной переменной. Объект рассматривается как функциональный преобразователь . Это соотношение называют статической характеристикой объекта. При идентификации ищется такая аппроксимация функции , что функционал . Это критерий качества – остаточная дисперсия выходной переменной относительно аппроксимирующей функции.

Для преодоления трудностей выбора аппроксимирующей функции её представляют отрезком разложения по заданной системе функций :

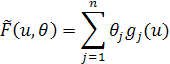
Если всю область переменных U разбить на подобласти, то в пределах отдельных подобластей входных переменных можно использовать простые функции . Простейшими функциями являются линейные.

Рассмотрим систему, имеющую m входов и один выход .

Предположим, что её можно описать уравнением

Модель будет построена, если будут найдены её коэффициенты. Воспользуемся серией измерений величин в r - моментов времени.

Обозначим , , тогда модель можно представить в векторной форме , где 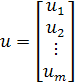; 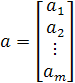. Поэтому r последовательных измерений удовлетворяют соотношениям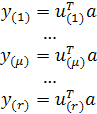

Определим вектор и матрицу

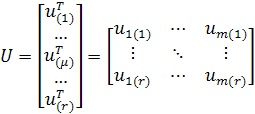
Уравнение модели имеет вид . Поскольку истинные значения a неизвестны, заменим их оценками, так что модель приобретёт вид .

Наилучшая (в смысле квадратических ошибок) оценка вектора a должна удовлетворять системе нормальных уравнений .

Система нормальных уравнений преобразуется к виду , что позволяет построить процедуру идентификации вектора на основе линейной регрессии и метода наименьших квадратов:

Этот подход легко обобщается на систему имеющую m входов и n выходов.

В этом случае модель представляется в виде ,

где

; ;

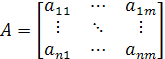
i – ая строка этого уравнения имеет вид

;

Подобно процессу с одним выходом для r измерений (r ≥ m+1) можно получить в матричной форме . Наилучшая оценка

;

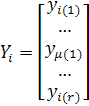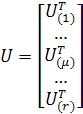
Представление нелинейных объектов с помощью ортогональных полиномов

Как статические, так и динамические процессы могут обладать нелинейными характеристиками, которые нельзя игнорировать. Для идентификации нелинейных процессов с помощью регрессии особого внимания заслуживают ортогональные полиномы. Они обладают следующими свойствами:

Вычисление коэффициентов полиномиального уравнения, аппроксимирующего нелинейный процесс, осуществляется быстрее, чем для не ортогональных полиномов.

Коэффициенты не зависят от порядка исходного уравнения, что поз- воляет построить модели нескольких порядков, коэффициенты полученные при низшем порядке остаются действительными и для высшего.

Рассмотрим следующую модель для одномерной системы:

- ортогональные полиномы т.е обладающие свойством

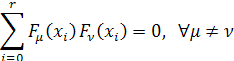
или в обобщённом виде

где r – число измерений, – целые положительные числа. Наиболее целесообразно использовать полиномы Чебышева:

Они обладают взвешенными свойствами ортогональности:

Несколько полиномов Чебышева низкого порядка приведено ниже:

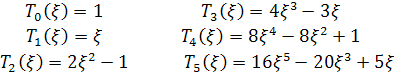
Справедливо рекуррентное соотношение

Аппроксимационный полином Чебышева для получают на основе минимизации S

что даёт:

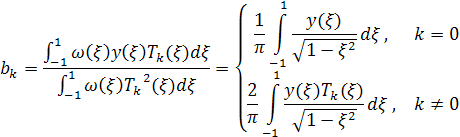
Так что . Коэффициенты разложения не зависят от m. При

полиномы Чебышева обладают свойством дискретной ортогональности для :

Здесь т.е. коэффициенты можно вычислить как минимизирующие выражение

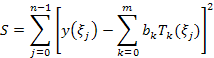
что даст

;

……

Линейные регрессии

Наиболее простое входно-выходное соответствие описывается линейным разностным уравнением

где – сигнал на входе; – сигнал на выходе; – помеха типа белого шума. Модель имеет следующий набор настраеваемых параметров

Введём многочлены ;

Тогда модель можно представить в виде:

где ;

Модель называется ARX – моделью, где AR относится к авторегрессионной части , а символ X обозначает дополнительный входной сигнал

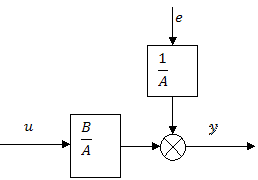
– авторегрессия с внешним входным сигналом. Диаграмма сигнальных потоков представлена ниже схемой.

Одношаговый прогноз для описания выходного сигнала определяется соотношением .

Расчитаем предсказатель для ARX - модели. Подстановка матриц даёт

Введём вектор

Тогда предсказатель можно записать в виде

Предсказатель представляет собой скалярное произведение известного вектора данных и вектора параметров . В статистике такую модель называют линейной регрессией, а вектор – регрессионным вектором. Ошибка предсказания принимает вид .

Критерий наименьших квадратов для линейной регрессии

где

Оценка вектора параметров………. По методу наименьших квадратов имеет вид:

Вопрос 18. Операторы систем

3.2. Операторы систем

Основной характеристикой системы является её оператор, определяющий механизм формирования выходного сигнала по данному входному сигналу.

Оператор детерминированной системы ставит в соответствие каждому входному сигналу один определённый выходной сигнал. Таким образом, оператор детерминированной системы отображает пространство входных сигналов в пространство выходных сигналов.

Оператор стохастической системы ставит в соответствие каждому входному сигналу определённое распределение выходного сигнала (зависящее от входного сигнала). Таким образом, оператор стохастической системы отображает пространство входных сигналов в пространство всех возможных распределений на пространстве выходных сигналов.

Входные и выходные сигналы непрерывной системы обычно представляют собой непрерывные ограниченные функции времени. Поэтому оператор детерминированной системы отображает пространство непрерывных функций в такое же пространство.

Пусть x(t) - входной сигнал детерминированной системы, представляющий собой непрерывную n – мерную векторную функцию времени t, y(t) – выходной сигнал, представляющий собой непрерывную m - мерную векторную функцию t . Обозначим A- оператор системы. Соотношение между входным и выходным сигналами детерминированной системы можно записать в виде y(t)=Ax(t). Эта краткая запись включает всю совокупность математических операций, которые надо выполнить над функцией x(t), чтобы определить функцию y(t).

Детерминированная система называется физически возможной, если значение её выходного сигнала y(t) в каждый момент t не зависит от значений входного сигнала при . Таким образом, значение выходного сигнала физически возможной системы y(t) в каждый момент t является функционалом от входного сигнала , заданного в интервале .

Стохастическая система называется физически возможной, если распределение значения её выходного сигнала Y(t) в любой момент t не зависит от значений входного сигнала при .

Детерминированная система называется устойчивой в данном режиме, если изменение её выходного сигнала y(t) в этом режиме остаётся сколь угодно малым при любом достаточно малом изменении входного сигнала x(t) Формально этотребование представляется в виде

Стохастическая система называется устойчивой в данном режиме почти наверное (с вероятностью 1), если изменение её выходного сигнала в этом режиме сколь угодно мало с вероятностью 1 при любом достаточно малом изменении входного сигнала .

Стохастическая система называется устойчивой в данном режиме по вероятности, если при любом существует такое ,что

при всех , удовлетворяющих условию .

Стохастическая система называется устойчивой в данном режиме в p-среднем, p>0 , если математическое ожидание в этом режиме остаётся сколь угодно малым при всех достаточномалых изменениях входного сигнала .

Из известного неравенства Чебышева

Следует, что стохастическая система устойчива по вероятности, если она устойчива в p-среднем. Точно также из устойчивости почти наверное вытекает устойчивость по вероятности. Из p-устойчивости при данном p следует p-устойчивость при всех меньших p. Обратное в общем случае неверно.

В задачах практики часто ограничиваются устойчивостью в среднем (p=1) или в среднем квадратическом (p=2)

Детерминированная система называется линейной, если при любых числах и при любых функциях

Это определяющее свойство линейных систем обычно называется принципом суперпозиции. Поэтому линейные системы можно определить как такие системы, для которых справедлив принцип суперпозиции. Оператор обладающий этим свойством называется линейным. Для того чтобы система была линейной, необходимо и достаточно выполнения следующих условий:

При суммировании любых входных сигналов соответствующие выходные сигналы суммируются;

При любом усилении входного сигнала без изменения его формы выходной сигнал усиливается с тем же коэффициентом, тоже не изменяя своей формы.

Для линейности системы необходимо, чтобы принцип суперпозиции соблюдался при любом числе слагаемых, при любом выборе постоянных и функций .

Система называется нелинейной, если принцип суперпозиции для неё не выполняется или выполняется только при некоторых вполне определённых . Оператор детерминированной нелинейной системы всегда нелинеен.

Примерами линейных операторов могут служить: оператор дифференцирования, линейный интегральный оператор, линейный интегро-дифференциальный оператор. К линейному интегральному оператору или к линейному интегро-дифференциальному оператору приводится оператор обыкновенного линейного дифференциального уравнения

Примерами нелинейных операторов могут служить: нелинейный интегральный оператор и оператор нелинейного дифференциального уравнения. Если среди уравнений, описывающих поведение системы, есть хотя бы одно нелинейное, то система не линейна.

Вопрос 19. Весовая функция динамической системы.

Весовая функция одномерной линейной системы

Представим входной сигнал одномерной линейной системы разложением на бесконечно малые мгновенные импульсы .

На основании принципа суперпозиции получаем следующее выражение для выходного сигнала ,

где индекс t у оператора A под знаком интеграла показывает, что этот оператор действует на функцию , рассматриваемую как функция t при фиксированном значении . Эта формула показывает, что для нахождения реакции линейной системы на произвольный входной сигнал достаточно знать её реакцию на единичный мгновенный импульс , действующий на неё в произвольный момент . Эта реакция зависит от момента действия импульса и текущего момента t. Функция , определяемая этой формулой, является исчерпывающей характеристикой линейной системы и называется её импульсной переходной (весовой) функцией. Пользуясь понятием весовой функции, можно записать выражение для выходного сигнала в виде

Для устойчивости системы необходимо и достаточно выполнение условия: .

Для линейной системы говорят об устойчивости без указания режима её работы, так она либо устойчива во всех режимах, либо неустойчива во всех режимах. Из общего критерия устойчивости выводятся частные критерии устойчивости для различных классов линейных систем.