Вопрос 13. Выбор рациональной модели

 

Выбор рациональной модели

 

Система Mw гомоморфна системе S, если при ее описании используется лишь часть характеристик системы S. В этом случае система Mw является моделью системы S. Переход от описания системы к её модели называется гомоморфизмом и может быть различным, т.е. одна и та же система может быть представлена различными моделями. Процесс построения моделей формально можно представить в виде следующей последовательности отображений:

 

S → W - переход от системы к её описанию;

W → Mw - переход от описания системы к модели, адекватной этому описанию;

Mw → M - переход от модели адекватной описанию к упрощённой модели;

M = {X, R}, где X - множество исходных данных; R - множество отношений на этих данных.

 

Определение:

 

Модель M* называется рациональной, если существует скалярная оценка сложности (например, время одного прогона модели):

,

где  C(M) - скалярная характеристика сложности модели.

M(r)∈M(r0) - множество моделей с допустимой собственной погрешностью r<r0 перехода Mw → M;

Обычно величину r представляют в виде r=(r1, r2, .... rm) - вектора собственной погрешности модели. Причем каждая из компонент состоит из суммы систематической и случайной ошибок:  ri=  ris +  rip,

где ris, rip - систематическая и случайная составляющие погрешности.

 

Модель M*, для которой выполняется  соответствие, собственной погрешности r и внесённой погрешности, вызванной неточностью описания системы допустимому значению r0,  называется корректной.

 

В ряде случаев удается ввести некоторую меру адекватности модели, т.е. указать способ сравнения двух моделей по степени успешности достижения цели с их помощью. В этом случае можно  количественно решить вопрос о зависимости меры адекватности от ее погрешности r и об  адаптации модели (т.е. подстройке параметров с целью повышения адекватности).

К математическим моделям предъявляют два основных требования:

Зависимости, связанные с моделью должны быть справедливы для всего интервала времени, на котором решается задача системного анализа.

Модель должна охватывать все управляющие и возмущающие воздействия, а так же выходные управляемые величины.

Вопрос 14. Недоопределённости в системе представления и обработки знаний

 

Недоопределённости представления и обработки знаний при моделировании

 

Недоопределённости отражают аберрации, возникающие во всякой системе знаний ввиду фундаментального различия между объективной реальностью и ее моделью. Отражая это различие между оригина­лом и его аппроксимацией, каждая развитая модель должна строиться с учетом ее «врожденных» свойств: принципиальной неполноты и принципиальной возможности ошибок и противоречий. С неполнотой всякой текущей системы знаний связывается, по край­ней мере, три аспекта:

 

Недоопределенность общих знаний: каждая типовая сущность в комплексе общих знаний о мире представляется, как прави­ло, не одной аппроксимацией, а системой аппроксимаций.

 

Недоопределенность конкретных знаний: в общем случае доступная информация о фрагменте реальности является непол­ной даже в рамках фиксированной системы общих знаний. Эта неполно­та может касаться типов объектов, значений величин.

 

Неоднозначность знаний, являющаяся результатом недоопределенности текущей модели конкрет­ного фрагмента действительности, приводит к необходимости принимать решения в условиях неопределенности.   Неопределённость может быть отображена следующей качественной последовательностью: детерминированное значение; значение, заданное на интервале; значение заданное дискретным распределением вероятностей; значение, заданное функцией распределения; значения, распределённые с плотностью, описываемой некоторым классом функций; значения информация о которых не конкретизирована.

 

 

Числовой мерой неопределённости для систем, задаваемых значениями своих определяющих показателей, является энтропия. Энтропия для некоторых распределений представлена в таблице:

 

Интервальное оценивание величин является первоначальным, фундаментальным представлением неопределённости знания. Интервальное оценивание обслуживает теория доверительных интервалов и интервальная математика. Доверительный интервал для математического ожидания нормально распределённой случайной величины с известной дисперсией

Доверительный интервал для математического ожидания нормально распределённой случайной величины с неизвестной дисперсией

Здесь дисперсия оценивается по выборке и используется квантиль распределения Стьюдента.

            Интервальная математика даёт слишком широкие интервалы. В технике их заменяют нормативными допусками.

Вопрос 15. Нормативное управление. Дефектность систем

 

Нормативное управление

 

            Нормативное управление – это задание допустимых интервалов изменения основных параметров системы. Нормативное управление – инструмент компенсации недоопределенности текущей модели управления. Считается, что в нормативных пределах осуществляются нормальные условия функционирования системы. Это основной вид управления для систем любой природы. Нормативные интервалы можно рассматривать как допустимую (приемлемую) степень неопределенности связанную с системой. Если некоторые параметры стохастические, то их доверительные интервалы должны покрываться нормативными, то есть текущее значение с приемлемой вероятностью должно находиться внутри нормативного интервала.

 

Система, параметры которой с некоторой вероятностью могут принимать значения вне нормативного интервала можно характеризовать уровнем дефектности. Определим показатель дефектности как функционал вида:

,

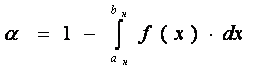где , – границы нормативного интервала фиксируемого параметра;   f(x) – плотность распределения оцениваемой величины.

Если дефектность системы нарастает, то система деградирует.

В терминологии интервалов:

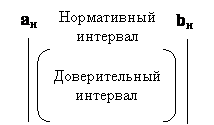
Очевидно, что для сохранения целостности система должна содержать механизмы (процедуры) управления дефектностью. Такими процедурами могут быть: профилактические осмотры и ремонты; самотестирование и "самолечение"; автоматизированное (ручное) режимное регулирование (подстройка) и т.д.

 

Закон распространения дефектности определяющих

технических параметров

 

Представим техническую систему математической конструкцией вида

 

,

 

где e – вектор независимых случайных величин.

Набор правил преобразования вектора входа s(t) в вектор выхода y(t) задаётся системным оператором T(t,e). На входы может подаваться детерминированный сигнал или случайный процесс, а на выходах деградирующего объекта имеем нестационарный случайный процесс. Нормативному управлению в таких системах подвергаются каналы входа или выхода, или только отдельные из них. Системный оператор практически никогда не управляется нормативно, его деградация фиксируется по выходу. Под деградацией системы понимается изменение статистических характеристик оператора такое, что вероятность нахождения значений хотя бы одной из компонент  yj(t), j=0,...,n вектора y(t) вне нормативных границ  aнj ± ej  увеличивается:

 

, .

 

Целью является  нахождение вида функций , которые принимаются за компоненты векторной модели деградации системы по наблюдаемым параметрам yj(t).

Аналитическое решение этой задачи может быть получено для линейного детерминированного дифференциального оператора со стационарным гауссовским процессом на входе. В этом случае на каждом выходе yj(t) наблюдается нормальный процесс с параметрами:

 

 

где   ms, Ks  - математическое ожидание и корреляционная функция процесса на входе.

Модель деградации системы по показателю yj(t) имеет вид

 

,

 

где   - интегральная функция распределения нормального процесса.

Нестационарность функции распределения стохастических параметров оператора приводит к тому, что теоретическая функция распределения выходного сигнала не может быть полностью восстановлена даже при стационарности входного процесса. Модель деградации и оценка порога наблюдаемости должны быть построены эмпирически. Эмпирическая модель деградации имеет вид

 

,

 

где  - эмпирическая функция распределения, построенная по выборке объёма N.

Объём выборки должен обеспечивать минимальную статистическую и динамическую погрешности. Это противоречивое условие удаётся выполнить, подбирая соответствующую частоту дискретизации при регистрации наблюдаемой величины. Некоторые аналогово-цифровые преобразователи (например, АЦП Е330) позволяют программно управлять частотой дискретизации. Для таких устройств:

 

.

 

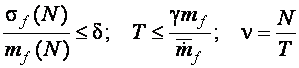Здесь объём выборки N находится из допустимой статистической погрешности d, продолжительность измерений выбирается по величине динамической погрешности g, а затем оценивается частота дискретизации n.

Из приведённых выражений следует, что для процессов с медленным временем среднее значение первой производной матожидания  функции  мало и частота дискретизации может быть минимальной. Напротив, для быстропеременных процессов её значения могут приближаться к частотному порогу АЦП.

В качестве главного компонента порога наблюдаемости примем величину , которую удобно трактовать как отношение шум/сигнал. Вторым компонентом является показатель, связанный с нестационарностью входного сигнала.Влияние тренда статистических характеристик входного процесса на эмпирическую модель деградации тем значительнее, чем больше коррелированность между входным и выходным сигналами. Выражение для расчёта порога наблюдаемости имеет вид

 

,

 

здесь  - коэффициент корреляции между входом и выходом. Порог наблюдаемости деградации системы пропорционален коррелированности входа и выхода и величине отношения шум/сигнал. Построение моделей деградации по входному и выходному сигналам даёт возможность идентифицировать нестационарные динамические системы, в том числе с нелинейными системными операторами.

Рассмотрим пример, когда системный оператор может быть представлен линейным регрессором, модель  имеет вид

 

 

где  - случайные коэффициенты с неизвестным законом распределения, зависящим от времени как от параметра;  - детерминированные функции.

Деградация отображается дрейфом этих коэффициентов. Дрейф связан не только с естественными законами старения и износа, но и с режимным регулированием, т.е. зависит от интенсивности потребления ресурсов. Экземпляр оборудования, на вход которого подаётся детерминированный сигнал, выход находится под нормативным управлением, а коэффициенты регрессора подчиняются нормальному закону распределения можно рассматривать, как пример генерации дефектности самим объектом, так как показатель дефектности входа равен нулю. Распределение сигнала на выходе также будет нормальным с параметрами:

 

;

 

 

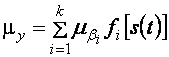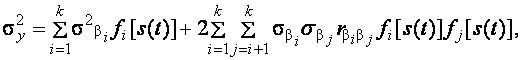
где  - математические ожидания, среднеквадратические отклонения и коэффициенты корреляции коэффициентов соответственно.

В метрологии это выражение называется законом распространения стандартных отклонений [20]. Дефектность данного экземпляра оборудования по параметру y(t) при нормативном интервале  представляется в виде:

 

.

 

Эта функция отражает изменение показателя дефектности за счёт деградации относительно бездефектных состояний, т. е. таких, которые описываются регрессором с детерминированными коэффициентами. Можно сформулировать закон распространения дефектности определяющих технических параметров:

 

«Показатели дефектности численно характеризуют распространение несоответствия на значение определяющего технического параметра. Это несоответствие  выражается через соотношение для распространения стандартных отклонений и математическое ожидание определяющего параметра».

 

В общем случае показатель дефектности выходного процесса вычисляется аналитически если:

1) распределение входного процесса известно.

2) системный оператор может быть представлен линейным регрессором с заданными распределениями коэффициентов.

3) функции fi дифференцируемы и обратимы (существует ).

Одним из фундаментальных интегралов, связанных с описанием  «неопределённости» значения параметра, является его энтропия. По одной и той же выборке значений определяющего технического параметра могут быть оценены его показатель дефектности и энтропия. На рисунке приведено отношение показателя дефектности к энтропии нормально распределённого определяющего технического параметра как функция отношения ширины доверительного интервала 2s к ширине нормативного.

Легко видеть, что при ширине доверительного интервала не больше нормативного это отношение линейно растёт - показатель дефектности чувствительнее энтропии к фактору деградации. Энтропия как индикатор более эффективна, когда ширина доверительного интервала превышает ширину нормативного в три раза. Вместе с тем принципиально важна аналогия эволюции дефектности и энтропии определяющих технических параметров для открытых неравновесных систем.

 

 

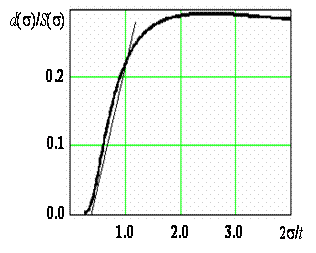
            Рис. Отношение показателя дефектности к энтропии нормально

            распределённого определяющего технического параметра как функция

            отношения ширины доверительного интервала  2s к  ширине

            нормативного: d(s)/S(s) (сплошная), линеаризованный участок (тонкая)

 

Поскольку деградирующая система является открытой то принцип Пригожина для открытых неравновесных систем, можно переформулировать следующим образом:

«Скорость возникновения дефектности в стационарном состоянии из-за необратимых процессов деградации элементов системы имеет минимальное значение».

Вопрос 16. Чувствительность модели

 

Чувствительность математической модели

 

Чувствительность является одним из основных свойств математической модели. Если модель содержит параметры, то анализ чувствительности представляет собой процедуру поиска ответа на вопрос: «А что произойдет с результатом моделирования, если параметры изменят своё значение?..». В большинстве случаев предпочтительной считается модель, обладающая малой чувствительностью к случайным возмущениям своих параметров. Такие модели называются робастными. Пусть результат моделирования представляется функцией общего вида:

,

где  - варьируемые параметры;  - решение уравнений состояния системы.

Цель анализа чувствительности определить полную производную таких функций от варьируемых параметров, т.е. найти .

            Используя правило дифференцирования сложной функции:

Обычно уравнение состояния системы записывается в следующем виде:

,

где - матрица отклика; - решение уравнений состояния системы; - матрица внешнего воздействия.

Дифференцируя обе части уравнения состояния, находим выражение для :

,

где ~ - обозначает переменную, которая должна быть в процессе частного дифференцирования постоянной.

            Подставляя это выражение в уравнение для чувствительности получаем общий вид основной формулы задачи анализа чувствительности:

В некоторых случаях результат моделирования можно представить в виде функционала, выражаемого с помощью интеграла, зависящего от параметра.

,

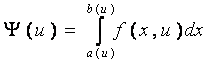
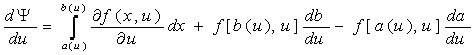Наиболее распространенный метод, исполь­зуемый для проведения анализа чувствительности - имитаци­онное моделирование. В качестве интегральных показателей, характеризующих результат модели, используются расчётные значения основных технических или эксплуатационных характеристик. Тогда, изменяя значения одного из параметров с некоторым шагом при постоянных значениях других, и каждый раз пересчитывая результат, получают функцию зависимости модели по этому параметру, её первая производная по параметру – чувствительность модели.