Тема 2. Теория моделирования

Вопрос 9. Классификация видов моделирования. (Классификационные, нормативные, аналоговые, натуральные модели)

ТЕМА 2. Теория моделирования

Классификация видов моделирования

Как уже было определено модель это объект-заместитель, воспроизводящий наиболее существенные, с точки зрения исследователя, свойства и характеристики системы. Моделированию предшествует работа по структуризации исходной проблемы. При использовании системного подхода к любой реальной проблеме относятся как к совокупности взаимосвязанных проблем. Используя для обозначения этой совокупности термин «проблематика», можно утверждать, что этап формулирования проблемы состоит в ограничении проблематики. Концептуальная модель системы, расположенная в вершине конуса разрешения представляет проблему, сформулированную в основных категориях и отношениях с элементами моделируемой системы и окружающей среды.

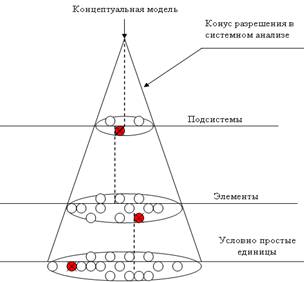
Иерархию моделей можно представить следующей схемой:

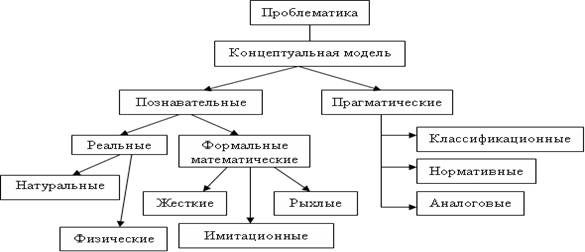
Условно разделим все модели на познавательные и прагматические, что соответствует делению целей на теоретические и практические. Различия этих двух классов моделей проявляется в их отношении к действительности.

Прагматические модели являются средством управления, рабочим представлением целей. Они отражают нормативный аспект отношения к действительности, и при обнаружении расхождений между реальностью и моделью их использование состоит в попытке приблизить реальность к модели. Прагматические модели включают: классификационные, нормативные, аналоговые.

Классификационные модели являются основополагающими, первичными, исходными формами знания и управления. Как правило, число классов задано. Целевой признак имеет значения в шкале имен классов (номинальная шкала) или в любой числовой шкале. Если заданы границы между классами, то имеем априорную классификацию; если границы требуется оценить по классификационным примерам, то производится распознавание образов по обучающей выборке. Каждому классу соотносится некоторое множество допустимых свойств и допустимых операций над его элементами. Класс служит шаблоном для его элементов (объектов). Например, деятельностью кампании можно управлять через систему должностных инструкций, разработанных для каждого рабочего места определённого типа.

Нормативные модели устанавливают нормативные значения для системообразующих индикаторов, инвариантов и базируются на: нормах, правилах, стереотипах, допусковом контроле и нормативных сценариях. Эти модели управляют системами через регламентацию их состояний и поведения. Например, устанавливается нормативный коэффициент запаса прочности (надёжности) изделий, исходя из предельных состояний материалов сферы их применения и режимов эксплуатации; оценку объёма продаж можно получить исходя из действующих норм рационального потребления; продолжительность выполнения работ регламентируется нормой воздействия вредных факторов на организм. Качество воды (воздуха), продуктов питания устанавливается по норме содержания в них определённых химических элементов.

Аналоговые модели основываются на эксплуатации частного сходства двух объектов. Наивысшим уровнем является полная аналогия. Для сложных систем возможны аналогии более низкого уровня. Для уникальных систем аналоги отсутствуют. В рамках этих моделей копируется поведение или содержание некоторой системы принятой в качестве аналога. Установлено, что подражание перспективному аналогу гарантирует сохранение на некоторый период перспективы успешного развития. Современная научная гипотеза создаётся, как правило, по аналогии с проверенными на практике научными положениями. Таким образом, аналогия связывает гипотезу (предсказание, основанное на небольшом количестве наблюдений) с экспериментом.

Познавательные модели являются формой организации и представления знаний. Они ориентированы на приближение модели к реальности. При реальном моделировании исследуются характеристики реальной системы целиком или её части. Такие исследования могут проводиться как в нормальных режимах эксплуатации, так и в специальных (экстремальных, ускоренных и т. д.).

Натурным моделированием называют исследование реальной системы. Например, обкатка машин, механизмов; испытание наработкой на отказ или до разрушения; испытание самолётов на соответствие их лётных характеристик проектным значениям; военные учения, имитация ликвидации последствий техногенных аварий и природных катастроф. Производственный эксперимент и комплексные испытания обладают высокой степенью достоверности.

Вопрос 10. Физическое моделирование

Физическое моделирование в его основе лежит теория подобия, устанавливающая отношения между изучаемой системой и её физической моделью. Системы (явления) называются подобными, если они различаются только масштабами. Если уравнения для двух явлений можно с помощью линейных преобразований привести к одному и тому же "эталонному" виду, то эти явления подобны. Во многих случаях критерии подобия можно установить непосредственно из соображений размерности. Они имеют вид безразмерных числовых комбинаций, построенных на основных размерностях систем.

Введение в теорию размерностей

Пи – теорема:

«Если между n параметрами, характеризующими изучаемый объект, существует зависимость, имеющая физический смысл, то эту зависимость можно представить в виде зависимости между их безразмерными комбинациями, где k – число независимых единиц измерения, через которые можно выразить размерности этих параметров. При этом определяет число независимых (не выражаемых друг через друга) безразмерных комбинаций, обычно называемых критериями подобия.»

Объекты, для которых равны значения соответствующих критериев подобия, считают подобными. Например, a, b, c – стороны треугольника однозначно определяют эту фигуру. Здесь n=3, k=1. Множество подобных треугольников можно задать значениями критериев подобия. В качестве таких критериев можно выбрать безразмерные отношения длин сторон b/a, c/a или любые два других независимых отношения. Так как углы однозначно связаны с отношениями сторон, и являются безразмерными величинами, то множество подобных треугольников определяется равенством двух соответствующих углов или равенством угла и отношением длин прилегающих к нему сторон. Для успешного применения П-теоремы к построению моделей технических систем необходимо располагать полным набором параметров.

Размерностью величины называют произведение степеней независимых единиц измерения физических величин, принятых в качестве основных (стандартных), например соответствующих систем единиц СИ (Systeme International): длина – (м), масса – (кг), время – (с), сила тока – ампер (А), температура – кельвин (К), сила света – кандела (кд), количество вещества (моль). Дополнительными являются радиан (ра) и стерадиан (ср).

Для принятой системы основных единиц измерения размерность любой величины может быть представлена единственным образом, в виде степенного одночлена

, (*)

где [Li] – размерности k величин, принятые в качестве основных единиц измерения, – некоторые показатели степени.

Наименьшую совокупность размерных и безразмерных величин, необходимых и достаточных для однозначного описания изучаемого объекта называют определяющими параметрами, величины зависящие от определяющих – определяемыми. Определяющие и определяемые параметры образуют совокупность основных параметров данного объекта.

Пусть рассматриваемый технический объект характеризуют n - основных параметров для каждого из которых справедливо уравнение (*)

Рассмотрим степенной одночлен

где zj – некоторые показатели степени, и найдём число – степенных одночленов этого вида при условии, что они являются независимыми и безразмерными.

При помощи (*) выразим размерность П, равную единице, через размерности k величин, принятых в качестве основных единиц измерения:

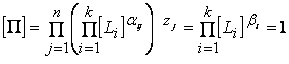Таким образом, условием равенства единице размерности степенного одночлена П является выполнения k равенств или

Это однородная система линейных алгебраических уравнений (СЛАУ) относительно n неизвестных zj с матрицей . Если ранг матрицы r то система имеет n-r линейно независимых решений, образующих фундаментальную систему решений. Таким решениям соответствуют ровно n-r независимых степенных одночленов Пq, q=1,…,n-r, размерности равной единице, поскольку показатели степени zj любого другого степенного одночлена П могут быть представлены линейной комбинацией решений из фундаментальной системы, а это означает, что П можно представить произведением степеней Пq. Ранг r матрицы , называемой матрицей размерностей, при n>k может принять наибольшее значение, равное числу k её строк. В этом случае из n основных параметров можно составить безразмерных комбинаций, т.е. степенных одночленов, что и является одним из утверждений П - теоремы. Но в общем случае r<k и поэтому формулировку П – теоремы следует уточнить:

«Имеющую физический смысл зависимость между n основными параметрами, характеризующими изучаемый объект, можно представить в виде зависимости между их независимыми безразмерными комбинациями, r – ранг матрицы размерностей, элементами которой являются показатели в выражениях вида (*) для размерностей этих параметров.

Второе утверждение этой теоремы состоит в том, что при помощи безразмерных комбинаций – критериев подобия – можно привести к безразмерному виду любую зависимость между n параметрами, имеющую физический смысл. В большинстве прикладных задач r=k, однако возможны случаи когда r<k, что заставляет при применении теории размерностей проверять ранг матрицы размерностей.

ПРИМЕРЫ

Математический маятник.

Пусть необходимо установить зависимость периода колебаний маятника от параметров: массы (m), длины нити (l), ускорения свободного падения (g), и угла (a). Размерности четырёх указанных параметров и периода колебаний T можно выразить через k=3 независимые стандартные единицы измерения: [T]=с, [m]=кг, [l]=м, [α]=0, [g]=м/с2 . Поэтому в силу П – теоремы из n=5 параметров можно оставить , причём угол является одной из них.

Величина m не является аргументом искомой зависимости поскольку её единица измерения не входит в какую либо из остальных и не может составить безразмерный комплекс. Остальные параметры образуют лишь одну независимую безразмерную комбинацию gT2/l.

Таким образом, согласно П – теореме, искомую зависимость можно представить в виде

или ,

где – некоторая функция угла.

Установить вид этой функции в рамках теории размерностей нельзя. В предположении бесконечно малых колебаний, её можно заменить на постоянное значение – нулевой член ряда Тейлора в точке равновесия. Тогда отношение подобия имеет вид

2. Теплопередача.

В технике известны фундаментальные критерии подобия, устанавливающие одинаковый характер обтекания, масса и тепло переноса для геометрически подобных тел.

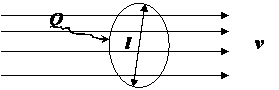Согласно П – теореме n=7 размерных параметров описывающих теплопередачу в потоке вязкой жидкости:

характерный размер тела [l]=м,

скорость потока [v]=м/с,

разность температур жидкости и тела [q]=[Tж-T0]=К,

тепловой поток [Q]=(кг×м2)/с3=Вт,

коэффициент теплопроводности [l]=Вт/м×К,

объёмная теплоёмкость [c]=кг/м×с2×К=Дж/м3К,

кинематический коэффициент вязкости [n]=м2/с.

можно выразить через k=4 независимые единицы измерения, т.е. ,число независимых безразмерных комбинаций равно . Две формы этих комбинаций имеют вид

где - Критерий Нуссельта;

- Критерий Рейнольдса; - критерий Прандтля; Pe=RePr – Критерий Пекле.

Критерий Нуссельта представляет отношение конвективного теплообмена к передаче тепла теплопроводностью в жидкости;

Критерий Рейнольдса характеризует течение вязкой жидкости;

Критерий Прандтля устанавливает связь теплопередачи с движением в жидкости.

Вопрос 11. Математическое моделирование

Математическое моделирование

В редакции выдающегося математика А.Н.Тихонова. "Математическая модель - приближённое описание, какого - либо класса явлений внешнего мира, выраженное с помощью математической символики. Процесс математического моделирования можно подразделить на четыре этапа.

Формулирование законов, связывающих основные объекты модели. Этот этап завершается записью в математических терминах, сформулированных качественных представлений о связях между объектами модели;

Исследование математических задач, к которым приводят математические модели. На этом этапе решается прямая задача, то есть получение теоретических следствий для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений;

Выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики (в пределах точности наблюдений). Если математическая модель такова, что ни при каком выборе своих характеристик не способна удовлетворить критерию практики, то эта модель непригодна для исследования данного явления. На этом этапе решается обратная задача, то есть находятся характеристики модели (параметрические, функциональные) таким образом, чтобы расчётные значения в пределах точности наблюдений совпадали бы с результатами измерений;

Последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели, опирающаяся на вновь полученные сведения.

Какова бы ни была природа рассматриваемой системы, её проблематика включает область проблем, от допускающих формализацию в виде задач математического программирования (такая постановка называется «жесткой»), до проблем не формализуемых, выраженных на естественном языке (такая постановка называется «рыхлой», а модели - «диффузными»). Естественно эти проблемы следует рассматривать по-разному, но в практике системного анализа имеется тенденция сводить все проблемы к одному типу, пользуясь правилом: Исследовать «рыхлую» проблему как «жесткую» гораздо опаснее, чем наоборот.

Имитационная модель – это формальное описание логики функционирования исследуемой системы и взаимодействия, отдельных её элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, и обеспечивающие проведение статистических экспериментов. Для имитационных моделей отсутствуют ограничения на область применения, наибольший эффект достигается при исследовании сложных систем, на функционирование которых существенное влияние оказывают большое количество случайных факторов.

Вопрос 12. Принципы моделирования

Принципы моделирования

Опыт разработки и использования математических моделей можно выразить следующими основными принципами моделирования:

Принцип информационной достаточности. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена её адекватная модель.

Принцип осуществимости. Создаваемая модель должна обеспечивать достижение цели исследования за конечное время с приемлемой вероятностью.

Принцип множественности цели. Модель должная отражать те свойства системы, которые существенно влияют на выбранный показатель эффективности. Модельный ряд в конусе разрешения обеспечивает заданный уровень детализации.

Принцип агрегирования. Система может быть представлена в виде агрегатов (подсистем), для адекватного описания которых пригодны некоторые стандартные математические схемы.

Принцип параметризации. Изолированные подсистемы могут быть заменены при моделировании значениями компонентов некоторого вектора играющего роль параметра системы. Параметризация может снижать адекватность модели.