Вопрос 5. Классификация систем

 

Классификация систем

Первичное знание о системах даёт их классификация. Классификацию проводят по самым различным основаниям: происхождению, устройству, назначению, и т.д. Классификации могут быть многоуровневыми, кратными, вложенными, однако ни одна из известных классификаций не  является  полной. Наиболее употребляемой является классификация по происхождению (рис. 6).

Рис. 6. Классификационное (по происхождению) дерево

 

Классификация систем по основаниям:

Число входов или выходов;

Свойства сигналов;

Свойства операторов.

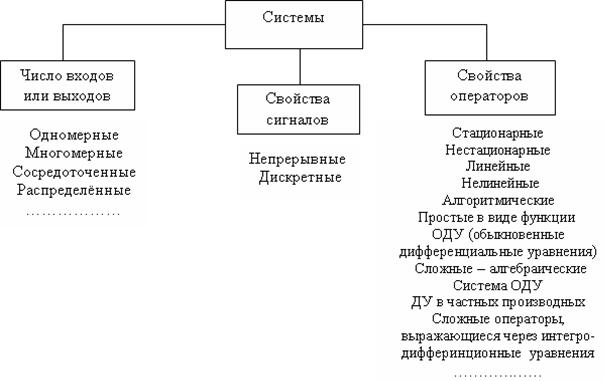
Рис.7. Классификационное (по трём основаниям) дерево

 

Системы, имеющие один вход и один выход, называются одномерными. Системы, имеющие несколько входов и несколько выходов, называются многомерными. Системы, у которых входы (выходы) представлены точками, называются сосредоточенными. Системы, у которых входы (выходы) распределены вдоль линии или являются поверхностями, называются распределенными. Если входные и выходные сигналы могут принимать непрерывное множество значений по величине и времени, то система относится к непрерывным; если сигнал поступает в дискретный момент времени (t) и может принимать конечное число значений, то такие системы – дискретные (импульсные). Системы называются стационарными, если их динамические свойства не меняются. Стационарность означает, что преобразование входных возмущений (сигналов) обладает инвариантностью относительно сдвига во времени (операторы для этих систем не зависят от времени). Реакция нестационарных систем на входное воздействие зависит как от текущего времени, так и от момента приложения входного возмущения. Если полнота классификации первого уровня логически ясна, то второй уровень на полноту не претендует.

 

Технические системы

 

Системы создаваемые людьми как средство образования искусственной окружающей среды обеспечивающей комфортное существование и защиту от природных факторов.

 

Основные свойства технических систем:

 

Имеют явно выраженную системообразующую границу и ограниченный во времени жизненный цикл;

Морфология (устройство) содержит всю информацию относительно функций систем и полностью их определяет. Априорная зависимость между морфологией и функцией  остается  неизменной на протяжении всего жизненного цикла системы;

Метаболизм (обмен с природной средой) веществом, энергией и информацией ограничен периодом функционирования;

Эволюция, как правило, принимает форму деградации.

 

Биологические системы

 

Природные системы способные управлять своей энтропией. Они осуществляют интенсивный метаболизм, за счёт которого усложняют морфологию и реализуют свою функцию. В своём развитии способны присоединять к себе часть окружающей среды.

 

Основные свойства биологических систем:

 

Ограниченный во времени жизненный цикл;

Эмерджентность (неделимость);

Коммуникативность;

Негентропийность;

Обратное влияние функции через накопление функциональной информации на морфологию;

Эволюция, как правило, принимает форму развития.

 

Эргатические системы

 

Эргатическая система – это совокупность машин и людей объединенных логикой производства и подчиненных общей цели – достижения его максимальной эффективности. Теория эргатических систем призвана давать общесистемные рекомендации по созданию функциональных структур и распределению ответственности между человеком и машиной за прогнозируемый конечный результат.

 

Основные свойства эргатических систем:

 

1. Эргатическая система активна (по крайней мере, потенциально ак­тивна) в некоторой непустой области пространства по­ведений и состояний системы;
2. Эргатическая система обеспечивает постоянство и независимость своей активности при различных состояниях внешней и внутренней сред;
3. Эргатическая система удер­живает основные свои показатели для своего нормального функцио­нирования в некоторых допустимых пре­делах.
4. Человек в эргатической системе во всех случаях стремится сохранять информированность о состоянии внешней и внутренней сред и при минимальном своем дей­ствии старается осуществить алго­ритм достижения заданного или максимального уровня эффективности всей системы;
5. Эргатическая система сохраняет основную функцию  при естественной вариативности функцио­нальных свойств, входящих в ее состав людей, маши­н, орудий труда, а также внешней и внутренней сред;
6. Эволюция эргатических систем определяется целевой ориентацией людей.

Вопрос 6. Эволюция систем

 

Эволюция систем

Свойства системы, фиксируемые в определённый момент времени, характеризуют её состояние. Формально это утверждение можно представить в следующей записи:

,

,

, , где  интервал наблюдения

Если рассматривать функционирование системы как последовательную смену состояний: , то это можно интерпретировать как переходы от точки к точки в  фазовом пространстве. Причём каждой реализации процесса соответствует своя фазовая траектория. Совокупность всех возможных состояний:  называется пространством состояний системы. Состояния детерминированной системы в момент  и  полностью определяется начальными условиями , входными воздействиями , внутренними параметрами системы , воздействиями внешней среды , которые имели место в течение промежутка наблюдения . Процесс перемещения по фазовой траектории обычно записываются с помощью следующих векторных уравнений:

 - уравнение состояния

 - выход (эндогенная переменная )

 

 

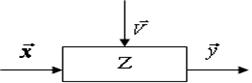
Часто эти уравнения удобно представить в эволюционной форме:

 

 

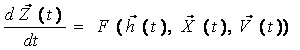
Эволюция (развитие) – постепенное, непрерывное количественное изменение параметров состояния, подготавливающее качественный переход, например, превращение в систему иного класса. Под эволюцией технической системы понимают изменение (вследствие технического прогресса) их морфологии обеспечивающее повышение эффективности, надёжности и т.д либо приводящее (при деградации) к накоплению необратимых дефектов.

Уравнение движения по фазовой траектории запишем в общем виде:

.

Очевидно, что вместе с Z(t) будет меняться во времени и любая другая динамическая величина F(t,Z(t)). Взяв от неё полную производную, по времени находим:

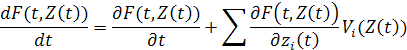
в операторном виде Ft = Dt[F(t, Z(t)]. Здесь Dt – дифференциальный эволюционный оператор.

            Теперь можно истолковать полную зависимость от времени как изменение Ft вдоль фазовой траектории. Например, для замкнутых стохастических систем такой подход позволяет записать уравнение эволюции полной функции распределения:

В соответствии с определением системы через фрейм эволюция, в общем смысле, представляется изменением во времени слотов этого фрейма:

 

Элементы. Число элементов может изменяться, в этом случае говорят о кинетике – о системах с переменным числом элементов (миграция, генетический дрейф, износ (старение), динамика популяций, формирование элитных групп).

 

Связи. Эволюция связей выделяет системы с переменной структурой. В таких системах изменяется число и "сила" связей, возникают новые общности внутри системы, имеющие собственные целевые ориентации. Различные формы спонтанной и инициированной реструктуризации, синтез подсистем,  возникновение диссипативных структур.

 

Границы – системы с переменной топологией системообразующей границы. Система-образующая граница изменяется при:

смене критерия принадлежности;

изменении действующих норм и правил;

смене целевой ориентации;

внешнем воздействии;

накоплении внутренних "напряжений", несоответствий, противоречий.

 

Цели – адаптивные системы. Как правило, для сложных систем характерна множественность целей, кроме того, изменение предпочтений – это средство адаптации к изменяющимся внешним и внутренним условиям. Множество целей может содержать такие, которые не выражаются формально и находиться друг с другом в следующих отношениях:

Цели нейтральны, поэтому по отношению к ним система рассматривается независимо.

Цели кооперируются, систему достаточно рассматривать по отношению к одной цели, а остальные достигаются одновременно.

Цели конкурируют, то есть достижение одной из них возможно лишь за счёт другой.

Реально, наблюдается некоторая смесь приведённых отношений, в этом случае систему рассматривают по отношению только к конкурирующим целям.

 

Процессы. Эволюция процессов отражает технологическое развитие. Оно может быть интенсивным или экстенсивным. Каждая ступень развития цивилизации формирует своё технологическое множество это: материалы, способы обработки, способы формообразования, соединения; виды энергии и энергетических обменов и т.д. В живой природе технологическое множество результат естественного отбора. Технологическое множество эволюционирует достаточно медленно, даже в условиях научно-технических революций системы успевают приспособиться.

 

Логика процессов. Эволюция логики достижения цели и форм организации процессов, как правило, определяется господствующей технологией, т.е. допустимой последовательностью необходимых действий для достижения заданной цели. Эта область архитекторов, конструкторов, производственников и т.д. В живой природе эволюция поведения определяется законом сохранения вида.

 

Ресурсы. Виды и качества ресурсов изменяются с изменением технологического множества. Сложные системы способны осуществлять эквивалентные взаимозамены (у живых существ это всеядность), подстраиваться под рыночные условия приобретения ресурсов. В большинстве случаев система стремится обеспечить максимальную эффективность реализации основной функции при минимальных затратах на ресурсы. Эволюция ресурсной базы управляет эволюцией большинства эргатических и биологических систем. Для технических систем расходование основного ресурса (безопасности) определяет срок службы. В процессе эксплуатации система расходует "безопасность" от некоторого исходного значения, при этом возможно пополнение (восстановление) ресурса как реакция на запрос. Как и для любого ресурса здесь возможен дефицит (префицит). В случае префицита говорят о запасе по безопасности, в случае дефицита о возникновении не компенсируемой опасности. Опасность материализуется в виде потока запросов не обеспеченных ресурсом. Предвестником аварии в этом случае является лавинообразное нарастание потока запросов не обеспеченных ресурсом, а следствием - исчерпание всех внутренних ресурсов и, как правило, разрушение системы.

Наиболее значимой в общесистемном смысле является эволюция сложности.        Сложность выражается через такие характеристики как число степеней свободы, законы сохранения, память, размерность, иерархия, длина цепей связи. Кроме того, динамическое поведение системы тесно связано со структурой отдельных элементов и способом их организации. Сложность системы можно определить как меру проявления недостатка информации для предельно - эффективного управления ее поведением.

Всеобщим законом эволюции является закон «самосохранения»:

«Система стремиться сохранить себя как целостное образование, и, следовательно, экономно расходует основной ресурс».

Вопрос 7. Вариационный принцип

 

Вариационный принцип. Системные инварианты

При описании систем постоянно употребляют превосходную степень прилагательных (наибольший эффект, наименьшие затраты, максимальная интенсивность). Это позволяет в сжатой форме выразить принцип, охватывающий широкий круг явлений. Математическая формулировка принципа содержащего прилагательное в превосходной степени обычно состоит в том, что интеграл от некоторой функции характерной для рассматриваемой системы принимают наибольшее и наименьшее значение при действительной эволюции по сравнению с любыми другими возможными способами эволюции.

Подынтегральное выражение является функцией, характеризующей рассматриваемую систему. Пусть некоторая система описывается набором показателей, зависящих от времени:

, где  - номер показателя,      .

 

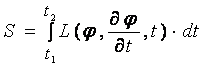Теорема:

Если выполняется:  на действительной траектории, то эволюция системы в пространстве показателей описывается уравнениями Эйлера-Лагранжа:

   

В механике L называют функцией Лагранжа или кинетическим потенциалом, функционал S называют «действие». Физически функция Лагранжа это:  , где T и U это кинетическая и потенциальная энергия, размерность действия в этом случае .

Все системы, которые подчиняются уравнению  с лагранжианом , называются лагранжевыми системами. Кроме этого вариационного принципа известны также другие, например два фундаментальных принципа, являющихся основой современной термодинамики:

 

Вариационный принцип Гиббса:

 

В состоянии термодинамического равновесия изолированная система имеет максимальную энтропию для всех возможных состояний с заданным уровнем энергии.

 

Вариационный принцип Пригожина:

 

Стационарное состояние системы, в которой происходит необратимый процесс, характеризуется тем, что скорость возникновения энтропии имеет минимальное значение при заданных внешних условиях препятствующих достижения равновесия.

Вопрос 8. Системные инварианты

 

Системные инварианты

Существует комбинация показателей, которая зависит только от начальных условий и не меняется в процессе движения:

                            

Такие функции называются инвариантами. Наиболее общим инвариантом является система единиц, которая используется при описании объекта. В физических явлениях существуют фундаментальные инварианты, которые определяют структуру пространства и времени. К таким инвариантам относятся масса, энергия, импульс, заряд. Все эти величины определяют некоторые законы сохранения (закон сохранения массы, энергии, импульса, заряда), а значение их состоит в том, что они ограничивают набор разрешенных состояний системы.

Наиболее просто эти инварианты выражаются для системы точек, находящихся в силовом поле. В таблице 1 приведены эти инварианты.

 

Таблица 1. Законы сохранения механики точек.

№ п/п	Наименование	Выражение	Определяемое свойство
1	Закон сохранения энергии		Однородность времени
2	Закон сохранения импульса		Однородность пространства
3	Закон сохранения момента импульса		Изотропия пространства

 

            Во многих  энергетических машинах используется непрерывный поток рабочего тела. Поток рабочего тела может обмениваться с окружающей средой теплотой и совершать работу при этом изменяется как внутренняя энергия рабочего тела, так и его механическая энергия. Уравнения динамики потоков составляются на основе уравнений сохранения массы, энергии и количества движения. Все они имеют общий вид

Накопление в объёме = Приток – Сток.

 

Уравнение сохранения массы

 

Рисунок 8. Схема для вывода уравнений сохранения потоковых величин.

 

 

Уравнение сохранения массы записывается для элементарного объёма рисунок 8.

            Уравнение сохранения массы имеет вид  . Выражения для соответствующих массовых расходов приведены в таблице 2.

 

Таблица 2. Компоненты массового расхода по осям в прямоугольной системе координат

 

Если сложить все приращения массового расхода в элементарном объёме и выразить изменение массы через плотность    то закон сохранения массы представится в виде

                  или                  

 

Уравнение сохранения энергии

 

Поток рабочего тела переносит тепловую и механическую виды энергии. Для полной энергии уравнение сохранения имеет вид

,

где

Поток тепловой энергии связан с переносом массы, обладающей удельной энергией килограмма вещества. Обозначив полную удельную энергию через e получим:        

Изменение потока тепловой энергии по осям координат (используя закон сохранения массы) можно представить в виде

            Поток механической энергии по координатам выражается через давление                                  .

Изменение потока механической энергии по осям координат представляется в виде            . Уравнение сохранения энергии имеет вид

,

где          - поток энергии в систему извне.                         

                                  

Уравнение сохранения количества движения

 

            Изменение количества движения элементарного объёма рабочего тела во времени равно сумме всех сил действующих на объём (закон Ньютона). Обычно рассматривают силы: тяжести, давления, трения, гидродинамического сопротивления. В полной форме закон сохранения количества движения может быть представлен в виде:

,

где  - коэффициент динамической вязкости среды.

            Во многих системах системообразующая граница является безусловным инвариантом. В этом случае уравнение является параметрическим заданием этой границы. Точка реальных состояний системы не может находиться вне этой границы, что задаёт ограничение на перемещение точки в фазовом пространстве. На рисунке 9 приведена схема допустимых областей для значений определяющих параметров некоторой системы.

 

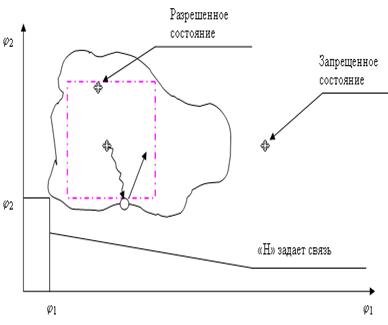
Рисунок 9. Схема областей состояний двух параметрической системы.

 

Для технических систем эта граница может быть очень сложной конфигурацией, поэтому часто используется нормативная системообразующая граница, которая имеет вид гиперпараллелепипеда максимального объёма, вписанного в допустимую область. Если вероятность приближения точки в некоторый момент к системообразующей границе возрастает, то применяют управляющее воздействие, которое возвращает систему в допустимое состояние.

Создание систем управления сложными технологическими объектами основывается на принципе инвариантности относительно внешних возмущений.

 

Общая теория систем ищет научные методы познания на пути учёта реально существующих внутренних взаимодействий и рассмотрения системы как целого. Системная сложность не подлежит упрощению или сведению целого к составляющим.