1. Общая схема системного анализа. Цели, задачи, основные категории.
2. Определение системы, основные свойства и закономерности
3. Системообразующая граница определение, свойства и примеры.
4. Классификация систем по происхождению. Биологические, технические и эргатические системы.
5. Эволюция систем (Основные уравнения, вариационный принцип, Системные инварианты). Неодарвинизм.
6. Идентификация систем.
7. Классификация видов моделирования по отношению к реальности. (Классификационные, нормативные, аналоговые, натуральные модели)
8. Математическое моделирование. Принципы моделирования. Выбор рациональной модели.
9. Недоопределённости представления и обработки знаний.
10. Чувствительность модели
11.Ранжирование целей. Метод анализа иерархий
12. Выбор стратегии. Минимаксный критерий.
13. Выбор стратегии. Критерий Байеса-Лапласа.
14. Выбор стратегии. Критерий Сэвиджа.
15. Моделирование структуры
16.Сетевая детерминированная модель.
17.Сетевая стохастическая модель.
18.Моделирование системообразующей границы.
19.Моделирование технических систем. Классификация по типу оператора
20.Имитационное моделирование.
21.Дана матрица решений А. Найти оптимальный вариант, применив (BL)-критерий
22. Дана матрица решений А. Найти оптимальный вариант, применив (ММ)-критерий
23. Дана матрица решений А. Найти оптимальный вариант, применив (S)-критерий
1. Общая схема системного анализа. Цели, задачи, основные категории.
Системой называют совокупность элементов, между которыми существуют те или др. связи. Система соответствующая некоторой проблеме может быть представлена следующим кортежем: S = ({элементы связи и системообразующие границы }, цель, процессы, логика достижения цели, организация процессов, ресурсы)
Системный подход - это некоторый общеметодологический принцип. Его гносеологический аспект – теория систем. Его прагматический аспект - системный анализ, а главным инструментом анализа является моделирование систем.
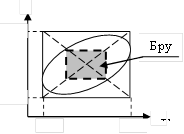
Общая схема системного анализа может быть такой как представлена на рис. 1.
Рис. 1
Реальность представляет собой слишком сложную структуру для того, чтобы явиться непосредственно объектом анализа. Часто говорят, что она неисчерпаема в познании. Категория "СИСТЕМА" является средством упрощённого представления реальной ситуации. Модель - объект-заместитель, воспроизводящий наиболее существенные, с точки зрения исследователя, свойства и характеристики системы. Модель позволяет определять динамические характеристики в ускоренном масштабе времени, осуществлять прогнозирование и оптимальное управление.
Характер системного подхода обеспечивает наибольшую простоту, а следовательно, и доступность при анализе с помощью системы моделей. Он состоит в том, что рассмотрение проблемы начинается с модели с низким разрешением и умеренными размерами.
2. Определение системы, основные свойства и закономерности.
Обычно системой называют совокупность элементов, между которыми существуют те или иные связи. Система соответствующая некоторой проблеме может быть представлена следующим кортежем: S = ({элементы связи и системообразующие границы}, цель, процессы, логика достижения цели, организация процессов, ресурсы)
Систему удобно представлять в виде схемы, состоящей из следующих блоков:
Первый блок: « ЭЛЕМЕНТЫ, СВЯЗИ, СИСТЕМООБРАЗУЮЩАЯ ГРАНИЦА». Отражает свойство целостности. Целостность – организованное множество элементов,их свойств и отношений, образующих структуру обеспечивающее определённое поведение в условиях окружающей среды.
Второй блок: « ЦЕЛЬ». Фиксирует момент достижения запланированного результата.
Третий блок: «ПРОЦЕССЫ». Множество возможных способов, действий, приемов, операций необходимых для достижения некоторой цели, состояния или получения некоторых свойств.
Четвертый блок: «ЛОГИКА ДОСТИЖЕНИЯ ЦЕЛИ». Последовательность действий и вытекающих из них событий, которые могут произойти с системой.
Пятый блок: «ОРГАНИЗАЦИЯ ПРОЦЕССА»
Представление жизненного цикла системы (возникновение - функционирование - уничтожение) в виде последовательности фаз или этапов, установление периода времени, в течение которого запланированная цель должна быть достигнута.
Шестой блок: «РЕСУРСЫ».
Источник (источники) «движущей (жизненной) силы» системы. Источники покрытия затрат.
Основные свойства и закономерности систем
1. Системы состоят из элементов
Элемент системы - это элементарная (с точки зрения данной системы) ее часть, дробление которой на более мелкие части становится нецелесообразным при изучении данной системы.
2. Элементы объединяются через связи, образуется структура
Связи - это достаточно прочные (долговременные) установившиеся контакты между различными элементами системы (каналы передачи действия).
Структура системы - это определенные взаиморасположение составных частей системы, ее устройство (строение).
3. Система определена на некотором допустимом для неё множестве состояний
Состояние системы - это значения параметров и характеристик в какой-либо промежуток или момент времени, которые фиксируются с целью её идентификации.
Равновесие системы - это такое состояние системы, когда функционирование всех элементов обеспечивает ее целостность и выполнение основных функций.
Устойчивость системы - это способность системы сохранять равновесие при различных отклонениях от обычных внешних и внутренних условий существования.
4. Система способна реагировать на внешние и внутренние воздействия.
Поведение системы - это развёрнутая во времени реакция системы на различные внутренние и внешние раздражители.
5. Система способна адаптироваться к внешним и внутренним воздействиям, изменяя своё устройство – эволюционировать.
Развитие - это способность системы постоянно изменять свое устройство в новое, более оптимальное и развитое. Обратный процесс - деградация системы.
Части систем имеющие аналогичные свойства называются подсистемами.
Системы, состоящие из некоторого числа подсистем, называют большими или сложными.
Девять свойств больших систем.
1. Неаддитивность. (ЭМЕРДЖЕНТНОСТЬ (emergence, от англ. "внезапное появление") - 1) особенность систем, состоящая в том, что свойства системы не сводятся к совокупности свойств частей, из которых она состоит, и не выводятся из них.)
2. Синергичность- это достижение максимального эффекта деятельности за счет сложений действий всех элементов и частей.
3. Мультипликативность.- это свойство проявляется в то, что отрицательные явления имеют явление не складываться, а перемножаются и даже возводится в степень
4.Внешняя целостность, обособленность от окружающей среды отображается системнообразующих границей.
5. Внутренняя целостность. Проявляется через структурную связанность.
6. Уникальность: каждая система этого класса не имеет полных аналогов поведения.
7. Слабопредсказуемость: никакое, сколь угодно подробное знание морфологии и функций элементов не позволяет определить фукций объекта; никакое сколь угодно подробное и точное знание поведения объекта на данном отрезке времени не позволяет точно предсказать его поведение в будущем.
8. Негентропийность или целенаправленность: система в состоянии управлять своей энтропией, способна устранять последствия внешних и внутренних случайных воздействий, выражает тенденцию сохранения и усиления основного процесса, ведущего к цели.
9. Устойчивость, если рассматриваемая система ведет себя почти так же как и соседнее.
Выделяют пять основных закономерностей систем:
1. у системы тем больше возможностей в выборе поведения, чем сильнее степень согласованности поведения ее частей;
2. в организационной структуре распределение компетенции по звеньям оптимально, если число взаимосвязей минимизируются;
3. для того чтобы создать систему, способную справиться с решением проблемы, обладающей определенным известным разнообразием, необходимо, чтобы система имела еще большее разнообразие или была способна воссоздать в себе это разнообразие:
Общее многообразие в поведении >= Многообразие возмущений / Многообразие управлений
4. в системе всегда существуют инварианты - количественное выражение предельных законов, которых образует оценки осуществимости, предельной жизнеспособности и потенциальной эффективности;
5. Поведение системы реализует действующий в системе вариационный принцип.
3. Системообразующая граница определение, свойства и примеры.
Системообразующая граница – это множество точек, образующая внешнюю поверхность физических систем. Систеообразующая граница связана с целью которая представляется системо образующим критерием (например, критерий принадлежности). Отражает свойство целостности. Целостность – организованное множество элементов, их свойств и отношений, образующих структуру обеспечивающее определённое поведение в условиях окружающей среды.
Свойства – определяет допустимые предельные состояния, вне системообразующей границы – система начинает затухать.
Пример – технические поверхности, контура, места выброса - трубы.
Системообразующая граница изменяется при:
- смене критерия принадлежности;
- действующих норм и правил;
- смене целевой ориентации;
- внешнем воздействии;
накоплении внутренних "напряжений", несоответствий, противоречий.
В технике чаще всего системообразующая граница задается в форме набора допуска на значение внутренних или основных параметров представление которое допускает отклонение от номинального значения только в определенном направлении.
4. Классификация систем по происхождению. Биологические, технические и эргатические системы.
Классификацию проводят по самым различным основаниям: происхождению, устройству, назначению, по безопасности и т.д. Классификации могут быть многоуровневыми, кратными, вложенными, однако ни одна из известных классификаций не является полной. Наиболее употребляемой является классификация по происхождению.
- Искусственные (Технические, информационные, транспортные и т.д.).
- Естественные (экологические, биологические, геологические и т.д.).
- Эргатические системы (производственные, экономические, хозяйственные).
В технологических науках широко распространенна классификация систем по основаниям: число входов, выходов; свойства сигналов, свойства операторов.
Технологические схемы - системы создаваемые людьми как средство образования искусственной окружающей среды обеспечивающей комфортное существование и защиту от природных факторов. Основные свойства: имеют явно выраженную системообразующую границу и ограниченность во времени жизненного цикла; устройство содержит всю информацию относительно функций систем и полностью их определяют; обмен с природной средой веществом, энергией и информацией ограничен периодом функционирования; эволюция как правило имеет форму деградации.
Биологические системы - природные системы способные управлять своей энтропией. Осуществляют интенсивный метаболизм, за счёт которого усложняют морфологию и реализуют свою функцию. В своём развитии способны присоединять к себе часть окружающей среды. Основные свойства: ограниченность во времени, неразделимость систем, коммуникативность, неэтропийность, эволюция.
Эргодические системы - это совокупность машин и людей объединенных логикой производства и подчиненных общей цели – достижения максимальной его эффективности. Эволюция эргатических систем определяется целевой ориентацией людей. Свойства – активна в некой непустой области поведений и состояний; сохраняет поведенческие функции при вариантности функциональных свойств входящих в ее состав людей, машин; эволюция определяется целевой ориентацией людей; человек в эгд. Системе стремится сохранить информацию о состоянии внешних сред и при минимуме своих действий стремится достичь максимум эффекта.

5. Эволюция систем (Основные уравнения, вариационный принцип, Системные инварианты). Неодарвинизм.
Эволюцию системы можно изучать по ее ракции на внешенее воздействие или по изменению некого показателя качества относительно базового или желаемого значения. Эволюция – это изменение внутренних параметров системы во времени. Во времени могут изменяться все блоки определения системы:
1. Эволюция связи выделяет системы с переменной структурой.
2. Эволюция границы – системы с переменной топологией системообразующей границы. 3. Эволюция цели – адаптивные системы.
4. Эволюция процессов отражает технологическое развитие.
5. Эволюция логики достижения цели и форм организации процессов определяется господствующей технологией
6. Эволюция ресурсов. Виды ресурсов, их качество меняются с изменением окружающей технологической среды.
Триада Дарвина: изменчивость, наследственность, отбор – представляет основные механизмы эволюции. Эволюционная предопределённость проявляется в том, что для сохранения основной функции подсистема должна оставаться согласованной с окружающей средой, т.е. с надсистемой.
Вариационный принцип. Системные инварианты
При описании систем постоянно употребляется превосходная степень прилагательных: наибольший эффект, наименьшие затраты и т.д. Математическая формулировка принципа, содержащего "прилагательное в превосходной степени", обычно состоит в том, что интеграл от некоторой функции, характерной для рассматриваемой системы, при происходящей в действительности эволюции системы принимает значение меньшее (или большее), чем при любой другой мыслимой эволюции.
Пусть
система характеризуется некоторым набором показателей, зависящих от параметров:
![]() ;
; ![]() В
число параметров может входить и время. Тогда интеграл, который требуется
минимизировать, можно записать в виде:
В
число параметров может входить и время. Тогда интеграл, который требуется
минимизировать, можно записать в виде:
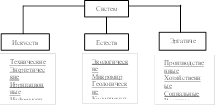 |
S – действия, L- функция
Лагранжа. Если в системе рассматривается вариационный принцип, то основное
уравнение является уравнением Эйлера. 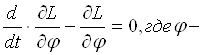 вектор
внутренних параметров системы.
вектор
внутренних параметров системы.
Он зависит от показателей, их производных по параметрам и параметров, которые являются переменными интегрирования. Отыскивая минимум этого интеграла можно получить дифференциальные уравнения с частными производными, управляющие показателями системы как функциями от параметров, т.е. закон эволюции системы.
6. Идентификация систем.
Идентификация это выявление и формальное представление существенных аспектов системы, обеспечивающее в удобной форме знания об этой системе. Идентификация через определяющие показатели (параметры, индикаторы) предполагает их использование в следующих областях:
1. интерпретация прошлого поведения и обобщение имеющихся знаний
2. предсказание будущего поведения
3. накопление старых и новых знаний,
4. получение таких знаний о системе, которые достаточны для автоматического управления.
При идентификации изучаемой системе сопоставляется система из некоторого класса эквивалентная данной. Обычно, изучаемой системе сопоставляется некоторая детерминированная или стохастическая система, для которой имеется возможность построить формальную или имитационную модель. В реальных условиях идентификацию нужно проводить быстро, при этом искусственные воздействия на систему часто недопустимы.
7. Классификация видов моделирования по отношению к реальности. (Классификационные, нормативные, аналоговые, натуральные модели)
Иерархию моделей можно представить следующей схемой:
Условно разделим модели на познавательные и прагматические, что соответствует делению целей на теоретические и практические. Различия этих двух классов моделей проявляется в их отношении к действительности. Прагматические модели являются средством управления, рабочим представлением целей. Прагматические модели включают: классификационные, нормативные, аналоговые.
Классификационные модели являются основополагающими, первичными, исходными формами знания и управления.
Нормативные модели устанавливают нормативные значения для системообразующих индикаторов, инвариантов и базируются на: нормах, правилах, стереотипах, допусковом контроле и нормативных сценариях.
Аналоговые модели основываются на эксплуатации частного сходства двух объектов. Копируется поведение или содержание системы принятой в качестве аналога. Подражание перспективному аналогу гарантирует сохранение на некоторый период перспективы успешного развития.
Познавательные модели являются формой организации и представления знаний. Они ориентированы на приближение модели к реальности. При реальном моделировании исследуются характеристики реальной системы целиком или её части.
Натурным моделированием называют исследование реальной системы. Например, обкатка машин, механизмов. Испытание наработкой на отказ или до разрушения.
В основе физического моделирования лежит теория подобия. Она устанавливает соотношение между раеальной системой и ее физической моделью. Системы называются подобными, если он отличаются только масштабами.
8. Математическое моделирование. Принципы моделирования. Выбор рациональной модели.
Математическое моделирование - это получение выводов при различных предположениях о структуре технологического множества, решение задач с технологическими множествами данного типа.
Математическая модель - приближённое описание какого - либо класса явлений внешнего мира, выраженное с помощью математической символики. Процесс математического моделирования можно подразделить на четыре этапа.
I. - формулирование законов, связывающих основные объекты модели. Этап завершается записью в математических терминах, сформулированных качественных представлений о связях между объектами модели;
II. - исследование математических задач, к которым приводят математические модели. Решение прямой задачи, т.е. получение теоретических следствий для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений;
III. - выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики (в пределах точности наблюдений). Если математическая модель такова, что ни при каком выборе характеристик этим условиям нельзя удовлетворить, то модель непригодна для исследования рассматриваемых явлений. Задачи, в которых определяются характеристики модели (параметрические, функциональные) таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений с результатами наблюдений, называются обратными;
IV. - последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели.
Принципы моделирования
1. Принцип информационной достаточности. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена её адекватная модель.
2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение цели исследования за конечное время с приемлемой вероятностью.
3. Принцип множественности моделей. Модель должная отражать те свойства системы, которые существенно влияют на выбранный показатель эффективности. Модельный ряд в конусе разрешения обеспечивает заданный уровень детализации.
4. Принцип агрегирования. Система может быть представлена в виде агрегатов (подсистем), для адекватного описания которых пригодны некоторые стандартные математические схемы.
5. Принцип параметризации. Изолированные подсистемы могут быть заменены при моделировании значениями компонентов некоторого вектора играющего роль параметра системы. Параметризация может снижать адекватность модели.
Выбор рациональной модели
Система Mw гомоморфна системе S, если при ее описании используется лишь часть характеристик системы S. В этом случае Mw является моделью системы S. Переход от описания системы к ее модели называется гомоморфизмом и может быть различным, т.е. реальная система S представима различными моделями Mw. Процесс построения моделей формально можно представить в виде следующей последовательности отображений:
S → W - переход от системы к её описанию;
W → Mw - переход от описания системы к модели адекватной описанию;
Mw → M - переход от модели адекватной описанию к упрощённой модели;
M = {X, R},
где X - множество исходных данных; R - множество отношений на этих данных.
Определение: модель M*
рациональна, если существует скалярная оценка сложности:![]() ,где C(M) - скалярная характеристика
сложности модели.
,где C(M) - скалярная характеристика
сложности модели.
M∈M(r0) - множество моделей с допустимой собственной погрешностью r<r0 перехода Mw → M;
Обычно величину r представляют в виде r=(r1, r2, .... rm) - вектора собственной погрешности модели. Причем каждая из компонент состоит из суммы систематической и случайной ошибок: ri= ris + rip,
где ris, rip - систематическая и случайная составляющие погрешности.
К математическим моделям предъявляются два требования: зависимости связанные с моделью должны быть справедливы для всего интервала времени для которого решается задача; модель должна охватывать все управляющие и возмущающие воздействия, а также выходные управляемее величины.
9. Недоопределённости представления и обработки знаний.
Недоопределённости отражают аберрации, возникающие во всякой системе знаний ввиду фундаментального различия между объективной реальностью и ее моделью. Отражая это различие между оригиналом и его аппроксимацией, каждая развитая модель должна строиться с учетом ее «врожденных» свойств: принципиальной неполноты и принципиальной возможности ошибок и противоречий. С неполнотой всякой текущей системы знаний связывается, по крайней мере, три аспекта:
Недоопределенность общих знаний: каждая типовая сущность в комплексе общих знаний о мире представляется, как правило, не одной аппроксимацией, а системой аппроксимаций.
Недоопределенность конкретных знаний: в общем случае доступная информация о фрагменте реальности является неполной даже в рамках фиксированной системы общих знаний. Эта неполнота может касаться типов объектов, значений величин.
Неоднозначность знаний, являющаяся результатом недоопределенности текущей модели конкретного фрагмента действительности, приводит к необходимости принимать решения в условиях неопределенности. Неопределённость может быть отображена следующей качественной последовательностью: детерминированное значение; значение, заданное на интервале; значение заданное дискретным распределением вероятностей; значение, заданное функцией распределения; значения распределённые с плотностью, описываемой некоторым классом функций; значения информация о которых не конкретизирована.
10. Чувствительность модели
Чувствительность является одним из основных свойств математической модели. Если модель содержит параметры, то анализ чувствительности представляет собой процедуру поиска ответа на вопрос: «А что произойдет с результатом моделирования, если параметры изменят своё значение?..». В большинстве случаев предпочтительной считается модель, обладающая малой чувствительностью к случайным возмущениям своих параметров. Такие модели называются робастыми. Пусть результат моделирования представляется функцией общего вида:
Ψ = Ψ(b, z(b)),
где b - варьируемые параметры; z(b) - решение уравнений состояния системы.
Цель анализа чувствительности определить полную зависимость таких функций от варьируемых параметров, т.е. найти dΨ/db.
Используя правило дифференцирования сложной функции:
![]() .
.
Наиболее распространенный метод, используемый для проведения анализа чувствительности - имитационное моделирование. В качестве интегральных показателей, характеризующих результат модели, используются расчётные значения основных технических или эксплуатационных характеристик. Тогда, изменяя значения одного из параметров с некоторым шагом при постоянных значениях других, и каждый раз пересчитывая результат, получают функцию зависимости модели по этому параметру, её первая производная по параметру – чувствительность модели.
11.Ранжирование целей. Метод анализа иерархий
Иерархия – тип отношений, основанный на предположении, что элементы системы могут группироваться в несвязанные множества.
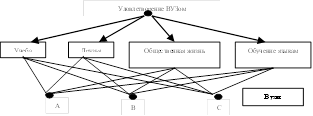 |
Математика метода анализа иерархий (МАИ)
Метод анализа иерархий, опирается на квадратные матрицы, представляющие суждения о парных сравнениях. С каждой такой матрицей ассоциируется её собственные векторы и соответствующие собственные знания. Для каждого элемента верхнего уровня производят попарно сравнение всех элементов более низкого уровня по их влиянию на этот элемент. Достигнутое при сравнении «согласие» (условный балл) помещаем в матрицу и для этой матрицы находим собственный вектор с наибольшим собственным значением. Собственный вектор обеспечивает упорядочивание приоритетов, а собственное значение является мерой согласованности суждений.
12. Выбор стратегии. Минимаксный критерий.
Критерий - это формальное представление цели. Понятию «критерий» обычно придается значение любого способа сравнения альтернатив. Критериальным может служить любой признак альтернативы.
Критерии являются количественными моделями качественных целей. Расхождения критериев и целей неизбежны. Необходимо добиться того, чтобы переход о качественных целей к критериям действительно приводил к движению в направление к заданным целям. Число критериев, достаточно полно «покрывающих» заданную цель, является мерой адекватности описания цели. Минимальное число критериев достигается, если они независимы.
Минимальный критерий соответствует позиции крайней осторожности:
![]()
оценочная функция
минимаксного критерия:![]()
Справедливо следующее
соотношение:![]()
В случае использования минимаксного критерия к матрице решений добавляется столбец, в строках которого стоят минимальные оценки полезностей, соответствующие данной строке. Из этого столбца выбирается вариант, соответствующий максимальному числу этого столбца.
В большинстве случаев построение множества вариантов Е требует значительных усилий. Но чтобы была обеспечена оптимальность выбираемого варианта, совокупность вариантов необходимо исследовать как можно более полным образом. Выбранные по ММ-критерию варианты полностью исключают риск, то есть принимающий решение не может столкнуться с худшим вариантом, чем тот, на который он ориентируется. Это свойство заставляет считать ММ-критерий одним из фундаментальных. В технических задачах он применяется чаще всего, но в экономических задачах строгий пессимизм ММ-критерия оказывается невыгодным.
Применение ММ-критерия оправдано, когда:
1. О возможности появления внешних состояний Fj ничего не известно.
2. Приходится учитывать появление внешних состояний.
3. Необходимо исключить какой бы то ни было риск.
13. Выбор стратегии. Критерий Байеса-Лапласа.
Критерий - это формальное представление цели. Понятию «критерий» обычно придается значение любого способа сравнения альтернатив. Критериальным может служить любой признак альтернативы.
Критерии являются количественными моделями качественных целей. Расхождения критериев и целей неизбежны. Необходимо добиться того, чтобы переход о качественных целей к критериям действительно приводил к движению в направление к заданным целям. Число критериев, достаточно полно «покрывающих» заданную цель, является мерой адекватности описания цели. Минимальное число критериев достигается, если они независимы.
Критерий Байеса – Лапласа BL
Пусть qj-вероятность появления внешнего события Fj.
Оценочная функция BL:![]() , где
, где ![]() -обобщённая
полезность:
-обобщённая
полезность: ![]()
![]()
![]()
Множество оптимальных вариантов:
![]()
Соответствующее правило выбора:
Матрица решений дополняется ещё одним столбцом, содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строках которых стоит наибольшее значение этого столбца.
Выбираем вариант, которому соответствует максимальное из этих чисел, то есть вариант Е1.
При использовании BL-критерия предполагается:
1. Вероятности qj известны и они не зависят от времени.
2. Решение реализуется много раз.
3. Для малого числа реализаций допускается некоторый риск.
Исходная позиция применяющего BL-критерий оптимистичнее, чем случай ММ-критерия. Однако она предполагает более высокий уровень информированности и достаточно длинные реализации.
14. Выбор стратегии. Критерий Сэвиджа.
Критерий - это формальное представление цели. Понятию «критерий» обычно придается значение любого способа сравнения альтернатив. Критериальным может служить любой признак альтернативы.
Критерии являются количественными моделями качественных целей. Расхождения критериев и целей неизбежны. Необходимо добиться того, чтобы переход о качественных целей к критериям действительно приводил к движению в направление к заданным целям. Число критериев, достаточно полно «покрывающих» заданную цель, является мерой адекватности описания цели. Минимальное число критериев достигается, если они независимы.
Введём обозначение ![]() :
: ![]() Оценочная
функция:
Оценочная
функция:![]()
![]()
![]()
Множество
оптимальных вариантов:![]()
Можно
интерпретировать ![]() как штрафы (потери), которые
возникают в состоянии Fj при замене оптимального для него варианта
на вариант Ei. Тогда
как штрафы (потери), которые
возникают в состоянии Fj при замене оптимального для него варианта
на вариант Ei. Тогда ![]() - максимальные
возможные по всем Fj потери в случае выбора варианта Ei.
В функции F эти потери минимизируются за счёт выбора варианта Ei.
- максимальные
возможные по всем Fj потери в случае выбора варианта Ei.
В функции F эти потери минимизируются за счёт выбора варианта Ei.
Соответствующее S-критерию правило выбора:
Каждый
элемент матрицы ![]() вычитается из наибольшего
результата
вычитается из наибольшего
результата ![]() соответствующего столбца. Разности
соответствующего столбца. Разности ![]() образуют матрицу остатков
образуют матрицу остатков ![]() . Эта матрица дополняется столбцом
. Эта матрица дополняется столбцом ![]() , выбираются те варианты, в строках
которых стоит наименьшее для этого столбца значение. S-критерий отражает
позицию относительного пессимизма. С точки зрения матрицы
, выбираются те варианты, в строках
которых стоит наименьшее для этого столбца значение. S-критерий отражает
позицию относительного пессимизма. С точки зрения матрицы ![]() он связан с риском, но с позиции матрицы
остатков
он связан с риском, но с позиции матрицы
остатков ![]() он от риска свободен.
он от риска свободен.
15. Моделирование структуры
 |
Обозначим вход элемента x = (x1,x2,... xm), а выход y = (y1,y2,... yn) тогда зависимость выхода y от входа x для элемента однозначна и определяется операторным y = T(x) или функциональным y(t) = f(t, x(t - t(t))) уравнением. Такое описание называется внешним. Здесь T - оператор преобразования; f - непрерывная и, по крайней мере, однократно дифференцируемая функция; t(t) - вектор-функция запаздываний, связанная в том числе, и с циклом переработки ресурса.
Структуру, состоящую из одного элемента можно рассматривать как простейшую и одновременно наиболее общую, представленную через своё внешнее описание.
X(1) = (x1(1),x2(1),……xk(1)) – входы системы; Y(1) = (y1(1),y2(1),……ym(1)) – выходы системы.
Связь выходы – входы задаётся системой функций таких, что:
Y(1) = F(1)(X(1)); X(1) = F(1)(Y(1)),
где
y1(1) = f1(1) (x1(1),x2(1),……xk(1)); x1(1) = f1(1) (y1(1),y2(1),……ym(1));
y2(1) = f2(1) (x1(1),x2(1),……xk(1)); x2(1) = f2(1) (y1(1),y2(1),……ym(1));
………………………………. ……………………………….
ym(1) = fm(1) (x1(1),x2(1),……xk(1)); xk(1) = fk(1) (y1(1),y2(1),……ym(1)).
Каждая из функций параметрически определена на множестве коэффициентов {ai(1)} Î A(1) для F(1) и {bj(1)} Î B(1) для F (1) ; i =1..m; j=1..k.
16.Сетевая детерминированная модель.
Организацию процесса в большинстве случаев моделируют с помощью сетевого календарного планирования.
Сетевой график, с точки зрения классификации графов, есть ориентированный связанный асимметричный граф, т.е. направленный граф. Пять основных параметров:
1. Наиболее раннее возможное время начала каждой работы;
2. Наиболее позднее допустимое время окончания каждой работы
3. Резервы времени каждой работы
4. Критический путь
5. Могут быть найдены важнейшие в каждый момент времени работы. Это работы, у которых резервы времени минимальны.
Формально эти параметры для сетевой детерминированной модели могут быть выражены через длину дуги (i, j), которую обычно обозначают символом tij тогда:
1. Наиболее ранее возможное время наступления j - го события (вычисляется прямой прогонкой):
![]()
2. Самое
позднее допустимое время наступления события i (вычисляется
обратной прогонкой):![]()
3. Резерв
времени:![]()
4. Полный
резерв времени работы (i,j): ![]()
5. Свободный
резерв времени работы (i,j): ![]()
17.Сетевая стохастическая модель.
Рассмотрим величины tij детерминированного сетевого плана как некоторые математические ожидания продолжительности. Математическое ожидание параметров детерминированной модели выражается как сумма математических ожиданий продолжительности работ Stij . Теорема о дисперсии суммы гласит, что дисперсия любого параметра А – это сумма дисперсий для всех дуг, ведущих к А:
![]() ,где A - некоторый
параметр сетевого графика.
,где A - некоторый
параметр сетевого графика.
Таким образом, остаётся оценить вероятность отклонения величины A от своего математического ожидания, если дисперсия уже известна. Эти формулы лежат в основе вероятностных расчётов, проводимых на сетевых графиках, которые в остальном могут оставаться детерминированными.
Для каждой операции определяются три оценки её длительности:
§ оптимистическая (минимальная) оценка, соответствующая наиболее благоприятным условиям выполнения (a);
§ пессимистическая (максимальная) оценка, соответствующая самым неблагоприятным условиям выполнения операции (b);
§ (m) – наиболее вероятная (нормальная) оценка, характеризующая усреднённые условия выполнения операции.
Предполагается, что в интервале [a, b] заключены все возможные продолжительности операции. Наиболее вероятная оценка m не обязательно совпадает со средней точкой отрезка. Три оценки отражают степень правдоподобия времени выполнения задачи.
Предполагается, что если операция выполняется большое число раз, причем ведётся регистрация всех данных, то график частот длительностей даёт ассиметричную кривую называемую β - функцией. Она может быть симметричной, асимметричной влево и асимметричной вправо.
18.Моделирование системообразующей границы.
Системообразующая граница – это множество точек, образующая внешнюю поверхность физических систем. Систеообразующая граница связана с целью которая представляется системо образующим критерием (например, критерий принадлежности). Отражает свойство целостности. Целостность – организованное множество элементов, их свойств и отношений, образующих структуру обеспечивающее определённое поведение в условиях окружающей среды.
Свойства – определяет допустимые предельные состояния, вне системообразующей границы – система начинает затухать.
В технике чаще всего системообразующая граница задаётся в форме набора допусков на значения внутренних или основных функциональных параметров системы. Пусть существует номинальное представление системы, то есть такое, которой соответствует заданному (желаемому) критерию качества при некоторых возможностях управления и некотором наборе внешних воздействий. Отклонение фактического качества от номинального допускается только в определенных пределах:
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]()
i= 1, …,m; j=1, …,n
где F – вектор критерия качества,
Еi – значения компонентов,
![]() – оператор,
– оператор,
![]() – множество операторов,
– множество операторов,
![]() – воздействие,
– воздействие,
![]() – множество воздействий,
– множество воздействий,
хj(t) – значение внутреннего параметра системы.
В
пространстве параметров существует связанная область ![]() такая,
что для всех точек множества
такая,
что для всех точек множества ![]() соответствующие
фактические значения F приемлемы. В каждый
момент времени состояние системы представляется вектором X(x1, x2,
…, xn). Для того чтобы система существовала в нормативных границах
необходимо, что бы с вероятностью PT случайный вектор X находился в
области
соответствующие
фактические значения F приемлемы. В каждый
момент времени состояние системы представляется вектором X(x1, x2,
…, xn). Для того чтобы система существовала в нормативных границах
необходимо, что бы с вероятностью PT случайный вектор X находился в
области ![]() в течение рассматриваемого времени T:
в течение рассматриваемого времени T:
![]()
Рассмотрим внешнее воздействие максимально не благоприятное для системы такое, что
![]()
с
геометрической точки зрения эта функция представляет гиперповерхность в
пространстве параметров. В этом случае область допустимой вариации параметров ![]() находим как пересечение этой
гиперповерхности с гиперплоскостью заданного качества:
находим как пересечение этой
гиперповерхности с гиперплоскостью заданного качества:
![]()
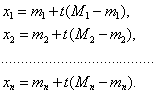 |
1.
Находим экстремальные значения для каждого параметра, принадлежащие
области ![]()
![]() ,
, ![]() .
.
2.
Через точки ![]() и
и ![]() проводим
плоскости, параллельные координатным, пересечение которых определит описанный
брус Bо.
проводим
плоскости, параллельные координатным, пересечение которых определит описанный
брус Bо.
3.
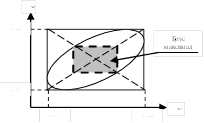
В описанном брусе B0 проводим диагонали:
4.
Находим точки пересечения диагоналей с границей области ![]() , т.е. решаем уравнение:
, т.е. решаем уравнение: ![]() .
.
5.
Соединив точки пересечения диагоналей с границей области ![]() , получим вложенный брус B, который
определит допуски на параметры системы.
, получим вложенный брус B, который
определит допуски на параметры системы.
При
реализации метода диагоналей необходимо последовательно решить две задачи:
построить описанный гиперпараллелепипед Bо и затем вложить в ![]() брус в соответствии с дополнительными
ограничениями.
брус в соответствии с дополнительными
ограничениями.
19.Моделирование технических систем. Классификация по типу оператора
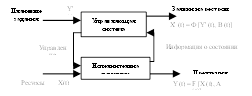
Технологические системы чаще всего представляются в виде модели содержащие множество входов, множество выходов и системы операторов.
![]()
Х, У –вектора.
В зависимости от вида системного оператора используется та или иная математическая модель.
Системный оператор:
- Детерминированный (алгебраическое уравнение, система алгебраических уравнений, дифференциальное уравнение, система с обыкновенным дифференциальным уравнением, интегро-дифференциальные уравнения);
- Стохастический оператор (одномерная функция распределения, многомерная функция распределения, операторы нечеткой логики, случайный процесс).
Исследование, составление, открытие возможных технологических процессов является предметом естественных и технических наук. При моделировании технологический процесс описывается как пара (x,r), где x-вектор выпуска различных продуктов; r-вектор затрат ресурсов. Совокупность всевозможных технологических процессов называется технологическим множеством (Т).
Т = {(x,r)i}
 |
Определение: Математическое моделирование - это получение выводов при различных предположениях о структуре технологического множества, решение задач с технологическими множествами данного типа.
Технологические процессы часто делят на:
- основные (технологические процессы производства);
- вспомогательные (изготовление инструмента, оснастки, производство энергоносителей, обслуживание и ремонт);
- обслуживающие (технический контроль, транспортные операции, складские операции).
При построении математической модели производства исходят из следующих принципиальных предположений:
- на технологическом множестве можно указать конечный набор основных (базовых) технологических процессов реализующих заданную структуру производства;
- интенсивность любого технологического процесса не зависит от других и определяется его собственными факторами. Выпуск производства определяется суммой выпусков отдельных технологий и пропорционален затрачиваемым ресурсам.
Тогда справедливо
следующее утверждение - любая структура производства представима в виде: ![]() ,
,
где ![]() - векторная производственная функция
выпуск-затраты;
- векторная производственная функция
выпуск-затраты;![]() - интенсивность
использования
- интенсивность
использования ![]() -го базового технологического процесса;
-го базового технологического процесса;
![]() - векторстрока выпуск-затраты
- векторстрока выпуск-затраты ![]() -го базового технологического процесса.
-го базового технологического процесса.
Пусть установлены нормативные задания по выпуску «продукции» технологического комплекса на некоторый период. В соответствии с этими заданиями планируется предполагаемое потребление ресурсов. Общая схема взаимодействия исполнительной и управляющих систем может выглядеть следующим образом, рис.:
В качестве функций fk (компоненты вектора регрессоров) в большинстве случаев при построении статистического математического описания промышленных объектов непрерывного действия используется модель с независимыми нормально распределенными, ошибками и равноточными измерениями. Она представляется отрезком ряда Тейлора в окрестности любой точки области определения факторов:
![]()
Такая модель позволяет провести полный статистический анализ эмпирического уравнения регрессии (построение доверительных интервалов для оценок, проверка различных статистических гипотез, определение надежности предсказания и т. д.). Предполагают, что всегда можно выбрать такую область эксперимента, в которой подобная модель окажется адекватной.
Адекватность идентификации предопределяется специфическими особенностями производственных условий.
К таким особенностям относятся:
- характер изменения технологических переменных;
- сравнительно низкая точность промышленных методов контроля и регистрации данных;
- узкие диапазоны изменения технологических переменных, зачастую соизмеримые с погрешностью контрольно-измерительной аппаратуры;
- значительные запаздывания в объекте, объясняющиеся отчасти транспортным перемещением реагентов, а отчасти инерционным характером самих процессов;
- влияние изменений окружающей среды;
- неконтролируемое изменение качественного состава сырья и переключение режимов при переходе с одного сорта продукции на другой и т. д.
В практических задачах, связанных с описанием промышленных объектов, информация о свойствах дрейфа – основа изучения их эволюции.
20.Имитационное моделирование.
Имитационная модель – это формальное описание логики функционирования исследуемой системы обеспечивающие проведение статистических экспериментов. Наибольший эффект такие модели дают в случаях сложных систем находящихся по влиянием случайных факторов.
Весь сетевой график будем считать вероятностной моделью, на которой оценки могут принимать любые значения, лежащие в указанных исполнителями пределах. На большом числе отельных реализаций сетевого графика, отличающихся тем, что величина tij на каждом из графиков случайно выбирается из своих законов распределения, оценивается критический путь и все параметры графика.
В разных реализациях, критическими могут оказаться различные пути на графике и можно ввести некоторую статистическую меру критичности пути, как отношение числа вариантов, в которых данный путь был критическим к общему числу разыгранных вариантов. Появляется возможность: выявлять иерархии критичности; оценивать среднее значение длительности выполнения проекта и её стандартное отклонение; указывать интервалы для резерва времени по каждой операции; выявлять операции, затягивание которых превращают субкритические пути в критические.
21.Дана матрица решений А. Найти оптимальный
вариант, применив (BL)-критерий
 0,7 0,2 0,1
0,7 0,2 0,1 ![]()
1,32
1,694
1,92
![]() ,
,
![]()
обобщённая полезность:
![]()
![]()
![]()
![]() =1,92
=1,92
Выбираем E3, т.е. 3 вариант.
22. Дана матрица решений А. Найти оптимальный
вариант, применив (ММ)-критерий
 0,6
0,6
0,12
0,4
![]()
max=0.6, следовательно выбираем 1 вариант
23. Дана матрица решений А. Найти оптимальный
вариант, применив (S)-критерий
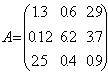
|
|
А |
В |
С |
|
А |
1 |
5 |
3 |
|
В |
15 |
1 |
13 |
|
С |
13 |
3 |
1 |
aij max
1.2 5.6 0.8 5.6
2.38 0 0 2.38
ПРОДОЛЖЕНИЕ 23 ВОПРОСА
0 5.8 2.8 5.8
max 2.5 6.2 3.7
![]()
![]()
![]()
![]()
![]() =2.38, следовательно выбираем 2-ой
вариант
=2.38, следовательно выбираем 2-ой
вариант