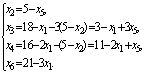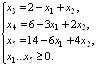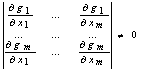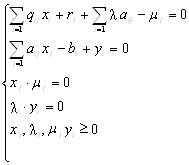1.Постановка задачи оптимизации. Понятие
целевой функции, допустимой точки (плана), оптимального решения. Классификация
методов математического программирования.
Моделью наз-ся усл-ый образ какого-либо объекта, приближенно
воссоздающий этот объект с помощью некоторого языка. В мат-их моделях объектами
явл-ся психич-ие, технологич-ие или экон-ие проц-сы, а языком – классические
или специально разраб-ые мат-ие м-ды. Т.о. мат-ую модель можно определить как
мат-ое опис-е исследуемого объекта в виде мат-их отнош-ий.
Выд-ют
3 осн. этапа мат-го моделир-я.
На
1-ом этапе формулир-ся цели и задачи исслед-я и пров-ся кач-ое опис-е объекта.
На
2-ом этапе строится мат-ая модель, осущ-ся выбор мет-ов реш-я поставленной
задачи, выбир-ся или разраб-ся прогр-ое обеспеч-е и подготавливаются исходные
данные. Кроме того проводится пров-ка адекватности построенной модели и оценка
устойчивости полученных рез-ов исх. задачи.
На
3-ем этапе осущ-ся проведение расчетов, обработка и ан-з рез-ов
Мат-ое
прогр-ие – это обл-ть мат-ки, разрабатывающая
теорию и численные м-ды реш-я экстремальных задач с ограничениями, т.е. задач,
связанных с нахождением max или min ф-ий неск-их перем-ых
Ф-ия,
экстремум к-ой ищется, наз-ся целевой ф-ей или критерием эфф-ти.
Модель
задачи мат-го прогр-ия включает в себя след. компоненты:
1)
n-мерный вектор x = (х1…хn)
перем-ых, воздействуя на к-ые можно изменить знач-я цел-ой ф-ии. Вектор х
наз-ся планом задачи или вектором упр-я, или стратегией;
2)
целевая ф-ия Z = Z(x)
или F = F(x), зависящая от указанных перем-ых и исследуемая на
экстремум, тот показатель, который нам нужно оптимизиорвать;
3)
ограничения, накладываемые на
обл-ть измен-я перем-ых. Эти ограничения берут из реальных условий протекания
процессов. Обл-ть изм-я перем-ых Ω(х) представляет собой нек-ую обл-ть n-мерного
простр-ва, задаваемое сис-ой ур-ий и (или) нер-в. Обл-ть Ω наз-ют обл-ю
допустимых знач-ий, а любой вектор х ' Ω – допустимым
планом задачи.
Т.о.
в общем виде задачу мат-го прогр-ия м. записать след. образом: F(x)® max (min), х ' Ω.
Оптимальным
решением (или оптимальным планом)
задачи ЛП называется решение Х = (х1, х2,
…, хп), удовлетворяющее указанным ограничениям, при котором
целевая функция принимает оптимальное (максимальное или минимальное) значение.
В
зав-ти от того, какой вид имеет цел-ая ф-ия и ограничения, задающие ОДЗ, выд-ют
разл. классы задач мат-го прогр-ия.
Если
и цел-ая ф-ия явл. линейной, а все ограничения им. вид линейных равенст или
неравенст, то задача наз-ся ЗЛП.
Если
хотя бы одна из ф-ий оптимизационной задачи не явл-ся лин-ой, то задача наз-ся ЗНП.
В
некоторых случаях переменные, участв. в задаче, могут принимать не любые
значения, а только целочисленные, то задача ЗЦелочисленногоП
Если
процесс принятия реш-я носит поэтапный хар-р и вектор упр-я на каждом шаге
опр-ся знач-ем цел-ой ф-ии на предыдущем шаге, то задача наз-ся задачей
динамического прогр-ия.
2.Задача линейного программирования.
Каноническая и стандартная форма ЗЛП. Геометрический смысл и графическое
решение ЗЛП.
В
общем виде задачу линейного программирования можно сформулировать следующим
образом: найти экстремум (максимум или минимум) целевой функции при ограничениях
при ограничениях
Если
целевая функция исследуется на max, а все неравенства им. вид ≤, то ЗЛП называется стандартной(нер-ва вида ≥ можно
превратить в ≤ *-1), если только равенства – канонической. Любая
задача линейного программирования может быть сведена к каноническому виду. Для
этого во все ограничения-неравенства необходимо ввести дополнительные переменные
xn+i,
положив: 
Общая задача ЛП имеет решение тогда и только тогда,
когда соответствующая ей каноническая ЗЛП имеет решение.
В
тех случаях, когда число перем-ых в задаче = 2, ЗЛП допускает графич-ое реш-е.
Пусть
дана задача
 (1.1)
(1.1)
Дадим геометрическую интерпретацию элементов этой
задачи. Каждое из ограничений задает на плоскости 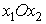 некоторую
полуплоскость. Полуплоскость – выпуклое множество. Но пересечение любого числа
выпуклых множеств является выпуклым множеством. Отсюда следует, что область
допустимых решений задачи (1.1) есть выпуклое множество.
некоторую
полуплоскость. Полуплоскость – выпуклое множество. Но пересечение любого числа
выпуклых множеств является выпуклым множеством. Отсюда следует, что область
допустимых решений задачи (1.1) есть выпуклое множество.
На рис. 1.1 представлены возможные ситуации, когда
область допустимых решений ЗЛП — выпуклый многоугольник (а), неограниченная
выпуклая многоугольная область (б), единственная точка (в), луч (г), отрезок
(д), пустое множество (е).
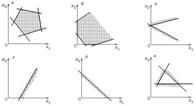
Если
ОДЗ пуста, то ЗЛП реш-я не имеет. Если ОДЗ состоит из единств-ой (×), то эта (×) и будет
явл-ся реш-ем ЗЛП.
Перейдем к геометрической интерпретации целевой
функции. Линией уровня целевой функции(линией условия) наз-ся
геометрич-ое место точек, в к-ом ф-ия принимает одно и то же знач-е. Если цел.
ф-ия линейна, то приравнивая ее к константе: 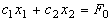 получаем
ур-ие прямой. Изменяя знач-е, характеризующее линию ур-ня F0 , получим семейство параллельных прямых.
получаем
ур-ие прямой. Изменяя знач-е, характеризующее линию ур-ня F0 , получим семейство параллельных прямых.
В общем случае направление возрастания функции
нескольких перем-ых в данной (×) хар-ся вектором,
составленным из частных производных и называемых градиентом:  . Если цел-ая ф-ия лин-на, то ее
частн. произв-ые равны коэф-ам при перем-ых и постоянны в любой (×).
. Если цел-ая ф-ия лин-на, то ее
частн. произв-ые равны коэф-ам при перем-ых и постоянны в любой (×). 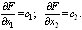
Учитывая св-ва градиента направл-е возрастания цел-ой
ф-ии хар-ся вектором с с коэфф-ми с1 и с2.
с = (с1 ; с2),
перпендикулярному линиям уровня.

При реш-и задачи на min нужно
двиг-ся в напр-и –с.
Из геометрической интерпретации элементов ЗЛП вытекает
следующий порядок ее графического решения.
1. С учетом
системы ограничений строим ОДР W. Если ОДР пуста, то ЗЛП не им.
решения, если она сост. из 1(.), то эта (.)-решение ЗЛП, если обл. не вырождена,
2 пункт;
2. Строим вектор
с = ( ;
; )
наискорейшего возрастания целевой функции – вектор градиентного направления.
)
наискорейшего возрастания целевой функции – вектор градиентного направления.
3. Проводим произвольную
линию уровня F=F0 (проще
всего провести линию F=0, перпендикулярную к вектору с).
4. При решении
задачи на максимум перемещаем линию уровня F=F0 в направлении вектора с
так, чтобы она касалась области допустимых решений в ее крайнем положении
(крайней точке) (на рис. 1.2 – до точки А4). В случае
решения задачи на минимум линию уровня F=F0 перемещают в антиградиентном
направлении (на рис. 1.2 – до точки А1).
5. Определяем
оптимальный план х* и
экстремальное значение целевой функции F*=f(x*).
3.Симплекс-метод решения ЗЛП, его сущность.
Алгоритм решения ЗЛП симплекс-методом. Критерий оптимальности решения.
Общий
смысл симплексного метода состоит в следующем: выбрав какую-либо начальную
точку, переходим к соседней с ней угловой точке так, чтобы знач-е цел-ой ф-ии
при этом не ухудшилось и продолжаем этот процесс до тех пор, пока не будет
достигнуто оптимальное реш-е.
Для реализации симплексного метода - последовательного
улучшения решения - необходимо освоить три основных элемента:
-
способ определения какого-либо
первоначального допустимого базисного решения задачи;
- правило перехода к лучшему (точнее, не худшему)
решению;
- критерий проверки оптимальности найденного решения.
Для
использования симплексного метода задача линейного программирования должна быть
приведена к каноническому виду, т.е. система ограничений должна быть представлена
в виде уравнений.
Решить симплексным методом задачу: 
при
ограничениях

Графическое решение задачи представлено
на рис.

х*=(6;4) F* = 24.
Решение. С помощью дополнительных неотрицательных
переменных перейдем к системе уравнений. В данном случае все дополнительные
переменные вводятся со знаком "плюс", так как все неравенства имеют
вид "£".
Получим систему ограничений в виде

Поскольку
число огран-ий > числа неиз-ых, то для нах-ия допуст. нач. реш-я (опорного),
необх-мо опр-ть базисные и свободные перем-ые.
I шаг.
Основные переменные:  . Неосновные
переменные:
. Неосновные
переменные:  .
.
Если
в сис-ме ограничений есть перем-ые, каждая из к-ыхв входит только в одно ур-е,
то для получ-я начального реш-я их можно взять за базисные. В кач-ве
базисн. перем-ых можно выбирать перем-ые, введенные при приведении ЗЛП к
канонич. виду.
Выразим
основные переменные и цел-ую ф-ию через неосновные:
(*) , откуда
, откуда 
Положив
неосновные переменные равными нулю, получим базисное решение (0; 0; 18; 16; 5;
21). Т.к. все компоненты найденного реш-я не отрицательны, нач-ое реш-е явл-ся
допустимым.
В
найденной точке значение функции  .
.
Т.о.
если при реш-и задачи на max какая-либо из свободных перем-ых входит в цел-ю ф-ию
со знаком «+», то найденное реш-е оптимальным не явл-ся, поскольку сделав эту
свободную перем-ую положительной, можно добиться увелич-я цел-ой ф-ии. Поэтому
необходимо эту переменную перевести в базисную, а вместо нее сделать свободной
какую-либо из базисных перем-ых.
Переводим
перем-ую х2 в базисную.
Каждое уравнение системы (*), кроме последнего,
определяет оценочное отношение - границу роста переменной х2,
сохраняющую неотрицательность соответствующей переменной. Эта граница
определяется абсолютной величиной отношения свободного члена к коэффициенту при
х2 при условии, что эти числа имеют разные знаки. Последнее
уравнение системы не ограничивает рост переменной х2, так
как данная переменная в него не входит (или формально входит с нулевым
коэффициентом). В этом случае условимся обозначать границу символом ¥. Такой же символ будем использовать, когда свободный член и коэффициент
при переменной в уравнении имеют одинаковые знаки, так как и в этом случае нет
ограничений на рост переменной.
Выбираем
ту строку, в которой оценочное отношение минимально. Эта строка наз-ся разрешающей
(опорной). Базисные перем-ые строки переводим в опорную.
Переводим
в свободную перем-ую х5.
II шаг.
Основные переменные:  . Неосновные
переменные:
. Неосновные
переменные:  .
.
Выразим
новые основные переменные через новые неосновные, начиная с разрешающего
уравнения:
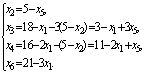 Второе базисное решение – (0;
5; 3; 11; 0; 21).
Второе базисное решение – (0;
5; 3; 11; 0; 21).
Выразив
линейную функцию через неосновные переменные на этом шаге, получаем: .
.
Значение
линейной функции  .
.
Однако
найденное реш-е не является оптимальным, т.к. коэф-т при х1
> 0 и увеличивая х1 , получим увелич-е цел-ой ф-ии.
х3 переводим в свободную, х1 в
базисную перем-ую.
III шаг. Основные
переменные:  . Неосновные переменные:
. Неосновные переменные:  .
.
После
преобразований получим:
(**)
Базисное
решение (3; 5; 0; 5; 0; 12). Выражаем линейную функцию через неосновные
переменные:  . Проверяем:
. Проверяем:  .
Третье допустимое базисное решение тоже не является оптимальным, поскольку при
неосновной переменной х5 в выражении линейной функции через
неосновные переменные содержится положительный коэффициент. Переводим х5
в основную переменную. При определении наибольшего возможного значения для х5
следует обратить внимание на первое уравнение в системе (**), которое не дает
ограничений на рост х5, так как свободный член и коэффициент
при х5 имеют одинаковые знаки. Из третьего ограничения
находим максимально допустимое значение х5 = 1. Третье
уравнение является разрешающим, и переменная х4 переходит в
неосновные.
.
Третье допустимое базисное решение тоже не является оптимальным, поскольку при
неосновной переменной х5 в выражении линейной функции через
неосновные переменные содержится положительный коэффициент. Переводим х5
в основную переменную. При определении наибольшего возможного значения для х5
следует обратить внимание на первое уравнение в системе (**), которое не дает
ограничений на рост х5, так как свободный член и коэффициент
при х5 имеют одинаковые знаки. Из третьего ограничения
находим максимально допустимое значение х5 = 1. Третье
уравнение является разрешающим, и переменная х4 переходит в
неосновные.
IV шаг.
Основные переменные:  . Неосновные
переменные:
. Неосновные
переменные: 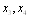 .
.
После
преобразований получим:
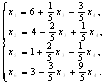
Базисное решение (6;
4; 0; 0; 1; 3).
Линейная
функция, выраженная через неосновные переменные, имеет вид  . Это выражение не содержит
положительных коэффициентов при неосновных переменных, поэтому функцию F
невозможно еще увеличить, переходя к другому допустимому базисному решению,
т.е. найденное решение – оптимальное. Значение
. Это выражение не содержит
положительных коэффициентов при неосновных переменных, поэтому функцию F
невозможно еще увеличить, переходя к другому допустимому базисному решению,
т.е. найденное решение – оптимальное. Значение 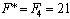 –
макс.
–
макс.
Теперь
можно в общем виде сформулировать критерии оптимальности решения при отыскании
максимума линейной функции: для того чтобы решение задачи на max было
оптимальным необходимо и достаточно, чтобы целевая функция при выражении через
свободные переменные не содержала положительных коэффициентов при свободных
переменных.
При определении минимума линейной функции Z возможны два пути:
1) отыскать максимум функции F,
полагая F = –Z и учитывая,
что  ;
;
2) модифицировать симплексный метод: на каждом шаге
уменьшать линейную функцию за счет той неосновной переменной, которая входит в
выражение линейной функции с отрицательным коэффициентом.
Можно
сформулировать критерий оптимальности при отыскании минимума линейной
функции: для того чтобы
решение задачи на min было оптимальным необходимо и
достаточно, чтобы целевая функция при выражении через свободные переменные не
содержала отрицательных коэффициентов при свободных переменных.
4.Симплекс-таблицы. Запись ЗЛП в виде симплекс-таблицы. Правила
пересчета симплекс-таблиц.
Реализация симплекс-метода значительно упрощается
при использовании таблиц специального вида, называемых симплекс-таблицами.
Рассмотрим задачу линейного программирования в
каноническом виде и предположим, что известно какое-либо допустимое базисное
решение этой задачи. Без ограничения общности можно считать, что базисный
минор, соответствующий неосновным (свободным) переменным задачи, расположен в
первых т столбцах системы ограничений. Тогда с помощью эквивалентных
преобразований систему можно привести к следующему виду:

Целевая функция, выраженная через свободные
переменные, имеет вид  .Построим симплекс-таблицу.
Строки симплекс-таблицы соот-ют базисным перем-ым и целевой ф-ии, а столбцы –
свободным перем-ым и свободным симплекс-таблицы ограничениям:
.Построим симплекс-таблицу.
Строки симплекс-таблицы соот-ют базисным перем-ым и целевой ф-ии, а столбцы –
свободным перем-ым и свободным симплекс-таблицы ограничениям:

Предположим, что задача линейного
программирования решается на максимум. Т.к. базисное решение является допустимым,
то все 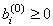 . Рассмотрим строку, содержащую
коэффициенты целевой функции, и проверим выполнение критерия оптимальности.
Возможны следующие варианты:
. Рассмотрим строку, содержащую
коэффициенты целевой функции, и проверим выполнение критерия оптимальности.
Возможны следующие варианты:
1.
В строке целевой функции нет положительных
коэффициентов. Тогда найденное допустимое решение является оптимальным.
2. В строке целевой
функции есть положительный коэффициент  .
Выделим в таблице соответствующий столбец (он называется разрешающим или
опорным).
.
Выделим в таблице соответствующий столбец (он называется разрешающим или
опорным).
3. Если в столбце 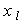 есть положительные коэффициенты, то в
качестве разрешающей выбираем строку с минимальным оценочным отношением
есть положительные коэффициенты, то в
качестве разрешающей выбираем строку с минимальным оценочным отношением 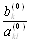 . Если положительных эл-ов в столбце
. Если положительных эл-ов в столбце  нет, то ограничений
нет и цел-ая ф-ия не ограничена сверху. Если полож-ые эл-ты есть, то в кач-ве
разреш-ей выбираем строку, в кот-ой оценочное отн-е минимально (н-р,
нет, то ограничений
нет и цел-ая ф-ия не ограничена сверху. Если полож-ые эл-ты есть, то в кач-ве
разреш-ей выбираем строку, в кот-ой оценочное отн-е минимально (н-р,  ). Элемент
). Элемент 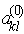 , стоящий на пересечении разрешающих
строки и столбца, называется разрешающим элементом.
, стоящий на пересечении разрешающих
строки и столбца, называется разрешающим элементом.
Опишем процедуру
перехода к новой симплекс-таблице и новому допустимому решению, увеличивающему
значение целевой функции. Для построения новой симплекс-таблицы необходимо
выполнить следующие операции:
1) поменять местами переменные  и
и
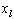 ;
;
2) на место разрешающего элемента поставить число  ;
;
3) на остальных местах разрешающей строки записать
соответствующие элементы исходной таблицы, деленные на разрешающий элемент  ;
;
4)
на свободные места разрешающего
столбца поставить со знаком «-» соответствующие элементы исходной таблицы,
деленные на разрешающий элемент

5)
остальные
элементы вычислить по правилу прямоугольника (рис. 2.3):
 .
.

6)
Для
полученной симплекс-таблицы снова проверяем критерий оптимальности и пересчет
продолжается до тех пор, пока не будет найдено оптимальное реш-е или не будет
показано, что ЗЛП реш-я не имеет.
5.Частные случаи симплекс-метода: вырожденное решение, альтернативный
оптимум, неограниченность целевой функции.
Рассмотрим особые
случаи, которые могут возникнуть при решении задачи линейного программирования
симплексным методом.
Неединственность оптимального решения (альтернативный оптимум)
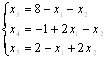
Решить
симплексным методом задачу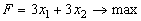 при ограничениях:
при ограничениях:


1
шаг. Основные переменные: х3, х4, х5. Неосновные
переменные х1, х2:.
 =>
=> 
х(0)=(0;0;8;-1;2)
2
шаг. Основные переменные: х1, х3, х4. Неосновные
переменные х2, х5:.

х(1)=(2;0;6;3;0)
F = 6-3х5+9х2®max F1=6
3
шаг. Основные переменные: х1, х2, х4. Неосновные
переменные х3, х5:.

х(2)=(6;2;0;9;0)
F = 6-3х5+9(2+1/3x5-1/3x3)=24-3x3®max
F2=24
Найденное реш-е оптимально, поскольку в цел-ой ф-ии нет
коэф-ов с положительными членами. Поскольку
в цел-ой ф-ии отсутствует неосновная переменная х5
(формально входит с нулевым коэффициентом), то изменение этой переменной не
повлечет за собой изменение линейной функции. Следовательно, зафиксировав х3
= 0 и изменяя х5 при соблюдении условие неотрицат-ти
остальных пер-ых будем получать другие допустимые точки с тем же знач-ем цел-ой
ф-ии, т.е. оптимальное реш-е в этом случае не единственно.
 , из системы уравнений можно получить все
множество оптимальных решений задачи.
, из системы уравнений можно получить все
множество оптимальных решений задачи.
Положим
для удобства х5 = t, где  [0; 9]. Тогда
множество оптимальных решений:
[0; 9]. Тогда
множество оптимальных решений:
x*=(6-1/3t ; 2+1/3t ; 0 ; 9-t ; t). F* = 24
Появление вырожденного
базисного решения
Решить симплексным методом
задачу  при
ограничениях:
при
ограничениях:

После
введения дополнительных переменных, которые возьмем в качестве основных,
получим:
I
шаг. Основные переменные:  . Неосновные переменные:
. Неосновные переменные: 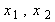 .
.
После
преобразований получим:
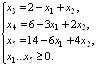
х(1)= (0; 0; 2; 6; 14) – допустимое базисное решение; 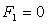 . Критерий оптимальности на максимум не
выполнен, поэтому переводим в основные переменную х1,
так как в выражение для F она входит с положительным коэффициентом: х1
= min{2; 6/3; 14/6} = 2. Оценочные
отношения в двух первых уравнениях совпадают,
поэтому в качестве разрешающего можно взять любое из них, например, первое.
. Критерий оптимальности на максимум не
выполнен, поэтому переводим в основные переменную х1,
так как в выражение для F она входит с положительным коэффициентом: х1
= min{2; 6/3; 14/6} = 2. Оценочные
отношения в двух первых уравнениях совпадают,
поэтому в качестве разрешающего можно взять любое из них, например, первое.
II
шаг. Основные переменные:  . Неосновные переменные:
. Неосновные переменные: 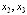 . Получим после преобразований:
. Получим после преобразований:

х(2)= (2; 0; 0; 0; 2) – вырожденное базисное
решение, основная компонента х4 = 0.
Функция цели, выраженная через неосновные переменные,
имеет вид: 
 . Переводя
переменную х2 в основные, получаем: х2 =
min{¥; 0; 1}= 0, поэтому на следующем шаге изменения функции цели
не произойдет, DF
= 0. Это нарушение принципа улучшения решения, который должен выполняться при
использовании симплексного метода, в связи с чем уточним данный принцип: каждый
следующий шаг должен улучшить или, в крайнем случае, не ухудшить значение
линейной функции.
. Переводя
переменную х2 в основные, получаем: х2 =
min{¥; 0; 1}= 0, поэтому на следующем шаге изменения функции цели
не произойдет, DF
= 0. Это нарушение принципа улучшения решения, который должен выполняться при
использовании симплексного метода, в связи с чем уточним данный принцип: каждый
следующий шаг должен улучшить или, в крайнем случае, не ухудшить значение
линейной функции.
III
шаг. Основные переменные: 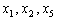 . Неосновные переменные:
. Неосновные переменные:  . После преобразований получим:
. После преобразований получим:

х(3)
= (2; 0; 0; 0; 2) – это
базисное решение тоже вырождено. Покомпонентно оно совпадает с х(2),
однако формально отличается набором основных переменных. Выражение линейной
функции через неосновные переменные имеет вид: 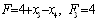 .
.
Вырожденное
допустимое реш-е появл-ся в той ситуации,когда минимальное оценочное отн-е
достигается более, чем в одной строке. В этом случае следующий шаг
симплекс-метода не приводит к улучшению цел-ой ф-ии.
Неограниченность
целевой ф-ии
Решить симплексным методом
задачу 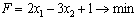 при
ограничениях:
при
ограничениях:

На
очередном шаге решения этой задачи симплексным методом получаем:
Основные
переменные –  ; неосновные переменные –
; неосновные переменные –  ;
;

Х = (5/3; 7/3; 0; 0; 4) – базисное решение;  .
.
Минимум не достигнут, так как критерий оптимальности
на это условие не выполнен: переменная х3 имеет отрицательный
коэффициент в выражении для F. Определяем х3 = min (¥,¥,¥) = ¥, т.к. в каждое из трех уравнений эта переменная входит с тем же
знаком, что и свободный член. Уравнения не ограничивают рост х3,
поэтому и значение функции F неограниченно и отрицательно, т.е.  .
.
Из рассмотренного примера следует вывод: если на
каком-либо шаге получаем, что во всех уравнениях системы бесконечны оценочные
отношения той переменной, которая переводится в основные, то задача не имеет
конечного оптимума ( , если задача на отыскание
максимума, и
, если задача на отыскание
максимума, и  , если задача на отыскание минимума).
, если задача на отыскание минимума).
Подводя итоги, можно
утверждать, что если система ограничений непротиворечива, то выполнение
конечного числа последовательных шагов симплексного метода либо приводит к
нахождению оптимального решения задачи (оно может быть неединственным), либо к
установлению того факта, что линейная функция не имеет конечного оптимума.
6.Отыскание
начального допустимого решения ЗЛП методом искусственного базиса. Определение
оптимальности найденного решения.
Применяется в тех случаях, когда выбор
базис. переем затруд. или одно из Ур-ний органич системы опред недопуст.
компоненту базисного решения.Выше был изложен алгоритм получения допустимого
базисного решения в случае, когда первоначальное базисное решение недопустимо.
Однако при расчете с помощью симплекс-таблиц удобнее пользоваться методом искусственного
базиса. Он заключается в следующем.
Рассмотрим ЗЛП в каноническом виде:
 (2.7)
(2.7)
Без ограничения общности можно считать, что все  . В противном случае умножим
соответствующее уравнение на –1. В каждое уравнение введем со знаком «+» свою
неотрицательную переменную
. В противном случае умножим
соответствующее уравнение на –1. В каждое уравнение введем со знаком «+» свою
неотрицательную переменную  , и рассмотрим
вспомогательную задачу линейного программирования:
, и рассмотрим
вспомогательную задачу линейного программирования:
 (2.8)
(2.8)
Определение
оптимальности найденного решения.
Отметим, что решение задачи
(2.8) всегда существует, т.к. ее множество допустимых значений  непусто (
непусто ( ), а
целевая функция ограничена снизу (
), а
целевая функция ограничена снизу (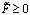 ). Решим задачу (2.8)
симплекс-методом.
). Решим задачу (2.8)
симплекс-методом.
Возможны следующие случаи.
1. 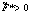 . Тогда можно показать, что
допустимое множество исходной задачи (2.7) пусто, т.е. эта задача не имеет решения.
. Тогда можно показать, что
допустимое множество исходной задачи (2.7) пусто, т.е. эта задача не имеет решения.
2. 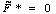 , и минимум целевой
функции
, и минимум целевой
функции  достигается в угловой точке
достигается в угловой точке
 (2.9)
(2.9)
допустимой
области  вспомогательной задачи. Тогда
вспомогательной задачи. Тогда
 (2.10)
(2.10)
угловая
точка допустимого множества исходной задачи, и ее можно использовать в качестве
начальной угловой точки при решении задачи (2.7) симплекс-методом.
Очевидно, что  тогда
и только тогда, когда все
тогда
и только тогда, когда все  равны нулю. Если
задача (2.8) невырождена, это означает, что переменные
равны нулю. Если
задача (2.8) невырождена, это означает, что переменные  являются
свободными для угловой точки (2.9). Опустим столбцы, соответствующие этим
переменным в окончательной симплекс-таблице, составленной при решении задачи
(2.8). Полученная в результате этого таблица будет соответствовать системе
ограничений задачи (2.7), разрешенной относительно переменных, являющихся
базисными для угловой точки (2.9). Поэтому остается заменить в этой таблице
последнюю строку на строку коэффициентов целевой функции исходной задачи,
выраженной через свободные переменные, и продолжить ее решение
симплекс-методом, выбрав точку (2.10) в качестве начальной угловой точки.
являются
свободными для угловой точки (2.9). Опустим столбцы, соответствующие этим
переменным в окончательной симплекс-таблице, составленной при решении задачи
(2.8). Полученная в результате этого таблица будет соответствовать системе
ограничений задачи (2.7), разрешенной относительно переменных, являющихся
базисными для угловой точки (2.9). Поэтому остается заменить в этой таблице
последнюю строку на строку коэффициентов целевой функции исходной задачи,
выраженной через свободные переменные, и продолжить ее решение
симплекс-методом, выбрав точку (2.10) в качестве начальной угловой точки.
Если вспомогательная задача (2.8)
вырождена, то некоторые из переменных  могут
оказаться базисными. Тогда эти переменные следует перевести в свободные с
помощью холостых шагов симплекс-метода (см. п. 2.3). После этого исходная
задача (2.7) решается, как описано выше.
могут
оказаться базисными. Тогда эти переменные следует перевести в свободные с
помощью холостых шагов симплекс-метода (см. п. 2.3). После этого исходная
задача (2.7) решается, как описано выше.
Замечание 1. Столбцы симплекс-таблицы, соответствующие
вспомогательным переменным  , удобно вычеркивать
на каждом шаге вместо того, чтобы исключать их одновременно в окончательной симплекс-таблице.
, удобно вычеркивать
на каждом шаге вместо того, чтобы исключать их одновременно в окончательной симплекс-таблице.
Замечание 2. Вспомогательные переменные можно вводить не во все
ограничения задачи (2.7), а только в те из них, которые определяют недопустимые
(отрицательные) компоненты базисного решения.
7.Двойственность
в линейном программировании. Связь между двойственными задачами. Основные
теоремы двойственности и их экономический смысл.
Пусть на предприятии решили рационально использовать
отходы основного производства. В плановом периоде появились отходы сырья т
видов в объемах bi единиц (i = 1,…, m).
Из этих отходов можно наладить выпуск п видов неосновной продукции. аij - норма расхода сырья i-го вида на
единицу j-ой (j
= 1,…, п) продукции, сj - цена
реализации единицы j-й продукции. Неизвестные величины: хj - объемы
выпуска j-ой продукции, обеспечивающие предприятию максимум выручки.
 (1)
(1)
Предположим, что на предприятии появилась возможность
реал-ции отходов некоторой орг-ции. Надо установить прикидочные оценки (цены) y1,…ym на эти отходы. Оценки должны быть установлены исходя
из следующих требований:
1) общую стоимость отходов сырья покупающая
организация стремится минимизировать;
2) предприятие согласно уступить отходы только по
таким ценам, при которых оно получит за них выручку, не меньшую той, что могло
бы получить, организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП:
 (2):
(2):
Переменные y1,…ym называются
двойственными оценками. Из (1), (2) можно показать, что если в качестве
прямой принять задачу (2) об определении оптимальных оценок на сырье, то
двойственной к ней будет задача (1) об определении оптимального плана выпуска
продукции. Имея матем. модель одной из задач, можно построить модель
двойственной к ней задачи. Задача, двойственная двойственной, совпадает с
исходной, поэтому безразлично, какую задачу принять в качестве прямой, а какую
– в качестве двойственной. Свойства двойственных задач:
1. Если прямая задача на max, то
двойственная к ней – на min, и наоборот.
2. Если в прямой задаче неравенство имеет вид  , то в
двойственной соответственно
, то в
двойственной соответственно  .
.
3. Число переменных прямой задачи = числу ограничений
двойственной, и наоборот..
4. Матрицы ограничений прямой и двойственной задач
являются транспонированными друг к другу.
5. Коэфф-ты целевой ф-ии прямой задачи явл-ся
свободными членами ограничений двойственной задачи, и наоборот.
6. Число ограничений прямой задачи = числу переменных
двойственной, а число ограничений двойственной = числу переменных прямой.
7. Все переменные в обеих задачах неотрицательны.
Основные
теоремы двойственности и их экономическое содержание
Теорема1(основное нер-во
двойс-ти) Для любых допустимых
планов х =  и
и
Y =
 прямой и двойственной ЗЛП справедливо
неравенство F(x)
прямой и двойственной ЗЛП справедливо
неравенство F(x) Z(y), т. е.
Z(y), т. е.
 (3.3)
(3.3)
Доказательство. Учитывая ограничения обеих ЗЛП, получаем

т. е. имеем неравенство (3.3), которое
называется основным неравенством теории двойственности.
Экономическое содержание
неравенства (3.3) состоит в том, что для любого допустимого плана производства х и любого допустимого вектора
оценок ресурсов Y общая созданная
стоимость не превосходит суммарной оценки ресурсов.
Теорема
2. (критерий оптимальности Канторовича). Если для некоторых допустимых планов х* и Y* пары
двойственных задач выполняется равенство z(x*) = f(y*), то х*
и Y* являются
оптимальными планами соответствующих задач.
Доказательство.
Согласно основному неравенству двойственности, для любого допустимого плана х прямой задачи и допустимого плана
Y* двойственной
справедливо неравенство z(x)  f(y*). Но по условию
f(y*). Но по условию
z(x*) = f(y*). Отсюда, в силу транзитивности отношений  и =, получим z(x)
и =, получим z(x)  z(x*). Так как х
- произвольный план, то z(x*) = max Z, т.е. х*
- оптимальный план прямой ЗЛП.
z(x*). Так как х
- произвольный план, то z(x*) = max Z, т.е. х*
- оптимальный план прямой ЗЛП.
Аналогично доказывается, что план Y* является оптимальным для
двойственной задачи.
Экономическое содержание
теоремы 3.2 состоит в том, что план производства х и вектор оценок ресурсов Y являются оптимальными, если цена всей произведенной продукции
и суммарная оценка ресурсов совпадают.
Теорема 3
(малая теорема двойственности). Для
существования оптимального плана любой из пары двойственных задач необходимо
и достаточно существование допустимого плана для каждой из них.
Теорема 4(основная теорема) Если одна
из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное
решение, причем экстремальные значения целевых функций равны. Если целевая функция одной из двойственных задач
неограниченна на ОДЗ, то другая задача не имеет решения, поскольку ОДЗ  .
.
Рассмотрим пару симметричных двойственных
задач представленных выше. Введем доп. переменные хn+1, ..., хn+m в прямую задачу и ym+1, ..., ут+п в двойственную, приводим
модели задач к каноническому виду. Теперь м/у переменными двойственных задач
можно установить соответствие, сопоставляя свободнвм переменным одной задачи
базисные переменные другой, и наоборот:

Экономическое содержание: если задача определения
оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима
и задача определения оценок ресурсов. Причем цена продукции, полученной при
реализации оптимального плана, совпадает с суммарной оценкой ресурсов.
Совпадение значений целевых ф-ций для соответствующих планов пары двойственных
задач достаточно для того, чтобы эти планы были оптимальными. Двойственные
оценки обладают тем свойством, что гарантируют рентабельность оптимального
плана и позволяют сопоставить и сбалансировать затраты и результаты системы.
Т.о., оптимальность плана означает точное воплощение в оценке произведенной по
этому плану продукции оценки всех израсходованных ресурсов, т.е. полное
отсутствие непроизводительных затрат.
Теорема 5 (о дополняющей нежесткости). Для того чтобы планы х* и у* пары двойственных задач были оптимальными, необходимо и
достаточно выполнение условий:
 ,
,  .
.
Экономическое содержание: двойственные оценки могут
служить мерой дефицитности ресурса. Если они  0,
то в силу условия дополняющей жесткости разница между расходом ресурса и его
запасом должна = 0, т.е. ресурс является дефицитным и расходуется в процессе
производства полностью. Если же расход ресурса < используемого запаса, т.е.
ресурс недефицитный, то в силу условия дополняющей жесткости, ее двойственная
оценка = 0.
0,
то в силу условия дополняющей жесткости разница между расходом ресурса и его
запасом должна = 0, т.е. ресурс является дефицитным и расходуется в процессе
производства полностью. Если же расход ресурса < используемого запаса, т.е.
ресурс недефицитный, то в силу условия дополняющей жесткости, ее двойственная
оценка = 0.
Теорема 6 (об оценках). Двойственные
оценки показывают приращение ф-ции цели, вызванное малым изменением
свободного члена соответствующего ограничения задачи математического
программирования, точнее . Двойственные оценки характеризуют
эластичность оптимального плана по каждому виду ресурсов, =>, перейдя от
дифференциалов к конечным приращениям можно получить
. Двойственные оценки характеризуют
эластичность оптимального плана по каждому виду ресурсов, =>, перейдя от
дифференциалов к конечным приращениям можно получить  оценку
изменения прибыли в зависимости от изменения ресурсов
оценку
изменения прибыли в зависимости от изменения ресурсов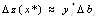 , при
, при  имеем
имеем 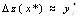 .
.
Экономическое содержание: двойственные оценки ресурсов
показывают как изменяется прибыль предприятия при изменении запасов этих видов
ресурсов на единицу.
8.Задача
целочисленного программирования. Классификация методов решения ЗЦП. Сущность
методов отсечения. Алгоритм Гомори решения полностью целочисленной ЗЦП.
ЗЛП, на все или некоторые переменные которой наложено
требование целочисленности, называются задачей целочисленного
программирования. ЗЦП в каноническом виде:

При этом J является
подмножеством множества N:  . Если J
совпадает с множеством N (J=N), т.е. условие целочисленности наложено на все
переменные задачи, то задача называется полностью целочисленной. Если J<N,
т.е. не все переменные должны быть целыми, то задача частично целочисленная.
Решение, полученное из округления, не всегда дает оптимальное решение ЦЗ, т.к.
1) полученная точка может
. Если J
совпадает с множеством N (J=N), т.е. условие целочисленности наложено на все
переменные задачи, то задача называется полностью целочисленной. Если J<N,
т.е. не все переменные должны быть целыми, то задача частично целочисленная.
Решение, полученное из округления, не всегда дает оптимальное решение ЦЗ, т.к.
1) полученная точка может  ОДЗ; 2) в ОДЗ может
найтись точка, обеспечивающая более оптимальное значение целочисленной функции. Методы
целочисленной оптимизации можно разделить на 2 основные группы: точные и
приближенные. К точным относятся методы отсечения и комбинаторные. Это универсальные
методы дискретной оптимизации. Кроме них, имеется много специальных точных
методов, учитывающих специфику задачи. Однако последние имеют слабую
сходимость. Среди приближенных методов наметились два направления:
ОДЗ; 2) в ОДЗ может
найтись точка, обеспечивающая более оптимальное значение целочисленной функции. Методы
целочисленной оптимизации можно разделить на 2 основные группы: точные и
приближенные. К точным относятся методы отсечения и комбинаторные. Это универсальные
методы дискретной оптимизации. Кроме них, имеется много специальных точных
методов, учитывающих специфику задачи. Однако последние имеют слабую
сходимость. Среди приближенных методов наметились два направления:
1) разработка детерминированных эвристических
алгоритмов, учитывающих специфику задачи;
2) использование случайного поиска в сочетании с локальной
оптимизацией.
Общая идея решения задачи
дискретного программирования методами отсечения состоит в следующем. Исходная
задача решается сначала без учета ограничений целочисленности. Если полученный
оптимальный план удовлетворяет условиям целочисленности, то задача решена. В
противном случае к ограничениям исходной задачи добавляется новое, обладающее
следующими свойствами:
1) является линейным
2) полученный нецелочисленный план нарушает это ограничение(отсечение
д. отсекать оптим. не целочисл. Решение);
3) любой целочисленный допустимый план исх. задачи
заведомо удовлетворяет и новому ограничению(отсечение не д. отсекать ни одной
целочисленной точки).
Затем задача реш-ся с учетом нового ограничения. В
случае необходимости добавляется еще одно ограничение и т. д.
Алгоритм метода Гомори для решения
полностью целочисленной ЗЛП:
1. Решается ЗЛП с отброшенным условием
целочисленности.
2. Полученное оптимальное решение (если оно существует)
проверяется на целочисленность. Если условие целочисленности выполняется по
всем переменным, то оптимальное решение ЦЗ совпадает с оптимальным решением
ЗЛП. Если это условие не выполняется хотя бы по одной переменной, то переходят
к 3-му этапу. Если ЗЛП оказывается неразрешимой, то ЦЗ тоже не имеет решения.
3. Строится дополнительное ограничение, отсекающее
часть области, в которой содержится оптимальное решение ЗЛП и не содержится ни
одного допустимого решения ЦЗ.
4. Возвращение к ЗЛП с отброшенным условием
целочисленности, но с расширенной системой ограничений, в которую включено дополнительное
ограничение, полученное на 3-ем шаге. К расширенной системе ограничений вновь
применяется симплексная процедура. Если найденное т.о. решение будет опять
нецелым, то формируется новое дополнительное ограничение и процесс вычислений
повторяется.
Алг-м Гомори позволяет за конечное число шагов прийти
к оптим-му целочисленному решению, если оно сущ-ет.
Формирование правильного
отсечения. После каждой итерации
симплекс-метода система ограничений ЗЛП имеет вид
 (4.1)
(4.1)
где {БП} - множество базисных переменных.
Если выполняется условие оптимальности
задачи, то все  Находим оптимальное решение.
Если, все компоненты оптимального плана целочисленны, то задача решена. Предположим,
что некоторые β0 - нецелые. Пусть компонента i0 - нецелая. Рассмотрим i0-равенство системы (4.1),
для которой выполняется условие оптимальности, т. е.
Находим оптимальное решение.
Если, все компоненты оптимального плана целочисленны, то задача решена. Предположим,
что некоторые β0 - нецелые. Пусть компонента i0 - нецелая. Рассмотрим i0-равенство системы (4.1),
для которой выполняется условие оптимальности, т. е.
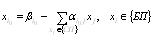 (4.2)
(4.2)
Перейдем к дальнейшему изучению уравнения
(4.2). Найдем целую и дробную части его коэффициентов  и
и
 . Т.к. по определению дробной части
числа
. Т.к. по определению дробной части
числа 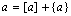 , получим:
, получим:
 (4.3)
(4.3)
Так как первое слагаемое равенства (4.3)
есть целое число, то, для того чтобы  было целым,
необходимо, чтобы второе слагаемое также было целым, т. е. Величина
было целым,
необходимо, чтобы второе слагаемое также было целым, т. е. Величина

должна быть целым числом. Так как 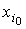 - координата допустимого целочисленного
решения, то
- координата допустимого целочисленного
решения, то  - всегда целое число. Покажем, что
- всегда целое число. Покажем, что  .
.
В самом деле, величина не может быть отрицательной. Из
определения дробной части числа следует, что
не может быть отрицательной. Из
определения дробной части числа следует, что  . Так
как
. Так
как
 - целое, то из предположения, что
- целое, то из предположения, что  > 0, должно следовать
> 0, должно следовать  , что противоречит определению дробной
части числа.
, что противоречит определению дробной
части числа.
Итак, доказано, что любое допустимое решение целочисленной задачи
должно удовлетворять неравенству
 (4.4)
(4.4)
Если после очередной
итерации окажется, что в оптимальном плане ЗЛП имеется несколько нецелых
координат, то для построения отсекающей гиперплоскости целесообразно выбрать
строку, содержащую свободный член с наибольшей дробной частью.
Признаком отсутствия целочисленного
решения служит появление в симплексной таблице хотя бы одной строки с дробным
свободным членом и целыми остальными коэффициентами, так как в этом случае
соответствующее уравнение не имеет решения в целых числах.
9.Постановка
транспортной задачи по критерию стоимости в матричной форме. Открытая и
закрытая формы ТЗ. Существование допустимого решения. Отыскание начального
распределения поставок методами северо-западного угла и наименьших затрат.
Постановка транспортной
задачи по критерию стоимости в матричной форме. Пусть имеется m поставщиков А1,…Аm,
обладающие запасами одного ресурса в количестве аi…am. Кроме того, имеется n потребителей этого ресурса В1,…Вn,
потребность каждого из которых составляет bj, j =
1,…n. Известно, что стоимость перевозки единицы ресурса от
i-ого поставщика j-му потребителю
составляет сij. Требуется найти оптимальный план перевозок, т.е.
определить количество хij-ого ресурса, перевозимого от i-ого поставщика
j-му потребителю т.о., чтобы суммарная стоимость всех
перевозок была минимальной.
Для построения
экономико-математической модели ТЗ рассмотрим матрицу

где хij
(i=1, т; j=1,
п) обозначает количество единиц груза, которое необходимо доставить из i-го
пункта отправления в j-й пункт назначения.
Матрицу X будем называть
матрицей перевозок. Предполагается, что все хij ≥ 0.
Удельные транспортные издержки (расходы) запишем в форме матрицы С=[ сij] и назовем ее матрицей тарифов.

Для наглядности условия ТЗ можно представить таблицей
(табл. 5.1), которую будем называть распределительной.
|
Поставщик
|
Потребитель
|
Запас груза ai
|
|
В1
|
В2
|
…
|
Вп
|
|
Затраты на перевозку единицы груза
|
|
А1
|
|
с11
|
|
с12
|
…
|
|
с1n
|
a1
|
|
x11
|
|
x12
|
|
x1n
|
|
|
А2
|
|
c21
|
|
c22
|
…
|
|
c2n
|
a2
|
|
x21
|
|
x22
|
|
x2n
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
|
Ат
|
|
cm1
|
|
cm2
|
…
|
|
cmn
|
am
|
|
xm1
|
|
xm2
|
|
xmn
|
|
|
Потребность в грузе bj
|
b1
|
b2
|
…
|
bn
|
|
|
|
|
|
|
|
|
|
|
|
|
Экономико-математическая модель ТЗ должна отражать все условия и цель
задачи в математической форме. Так, переменные хij должны
удовлетворять ограничениям по запасам, потребностям и условиям
неотрицательности. В математической форме эти условия можно записать так:
 (5.1)
(5.1)
Цель ТЗ -
минимизировать общие затраты на реализацию плана перевозок, которые можно
представить функцией
Модель ТЗ называют закрытой, если
суммарный объем груза, имеющегося у поставщиков, = суммарному спросу
потребителей. Если суммарный объем груза < или > суммарного спроса, то
модель называют открытой.
Открытая модель ТЗ м.б. сведена к закрытой путем:
введением фиктивного поставщика, если нехватает запасов или фиктивного
покупателя если запасов избыток
Условие равенства запасов и потребностей
является необходимым и достаточным условием существования допустимого решения
ТЗ (по критерию стоимости).
Правило «северо-западного угла».
Сущность: распределяем груз, начиная с загрузки левой верхней, условно
называемой северо-западной, клетки (1; 1), двигаясь затем от нее по строке
вправо или по столбцу вниз. В клетку (1; 1) заносим меньшее из чисел a1, b1, т. е. x11 = min (a1, b1). Если a1>b1, т. е. x11 = b1 и 1-ый
потребитель В1 будет полностью удовлетворен. В дальнейшем 1-й
столбец таблицы в расчет не принимается; в нем переменные хik =0 для i=2, т.Двигаясь вправо по 1-ой строке таблицы,
заносим в соседнюю клетку (1; 2) меньшее из чисел a1-b1, и b2, т. е. x12 = min (a1-b1, b2).
Если a1-b1<b2, то запасы первого поставщика исчерпаны и 1-ая строка
таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному
распределению запаса груза 2-го поставщика.
Если a1< b1, т. е. x11 = a1. При
этом запас 1-го поставщика будет исчерпан, а потому хik =0 для k= 2, п. 1-ая строка из дальнейшего рассмотрения
исключается. Переходим к распределению запасов 2-го поставщика. В клетку (2; 1)
заносим наименьшее из чисел (а2, b1- а1). Заполнив т.о. клетку
(1; 2) или (2; 1), переходим к загрузке следующей клетки по 2-ой строке либо по
2-му столбцу. Процесс распределения по 2-ой, 3-ей и последующим строкам
(столбцам) производится аналогично распределению по 1-ой строке или 1-му
столбцу до тех пор, пока не исчерпаются ресурсы. Последней заполняется клетка (т;
п).
Правило
«минимального элемента». Сущность: просматриваются тарифы табл. и в первую
очередь заполняется клетка с минимальным значением тарифа. При этом в клетку
записывается максимально возможное значение поставки. Затем из рассмотрения
исключают строку, соответствующую поставщику, запасы которого полностью
израсходованы, или столбец, соответствующий потребителю, спрос которого
полностью удовлетворен. После этого из оставшихся клеток таблицы снова
выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается,
когда все запасы поставщиков исчерпаны, а спрос потребителей полностью
удовлетворен. В результате получаем опорный план, который должен содержать т+п-1
загруженных клеток. В процессе заполнения таблицы могут быть одновременно
исключены строка и столбец. Так бывает, когда полностью исчерпывается запас
груза и полностью удовлетворяется спрос (вырожденная задача). В этом случае в
свободные клетки надо записать число 0 - «нуль-загрузка», условно
считая такую клетку занятой. Однако число 0 записывается в те свободные клетки,
которые не образуют циклов с ранее занятыми клетками.
10.
Метод потенциалов. Критерий оптимальности решения ТЗ. Экономический смысл
оценок свободных клеток. Перераспределение поставок. Определение единственности
решения.
Если план  транспортной задачи является
оптимальным, то ему соответствует система из m+n
чисел
транспортной задачи является
оптимальным, то ему соответствует система из m+n
чисел  , удовлетворяющих условиям
, удовлетворяющих условиям  для
для  и
и  для
для 
Числа  называются
потенциалами соответственно i-го поставщика и j-го
потребителя.
называются
потенциалами соответственно i-го поставщика и j-го
потребителя.
Из теоремы следует, что для оптимального плана ТЗ необходимо выполнение
условий:
1)
каждой занятой клетке в распределительной таблице соответствует сумма
потенциалов, равная тарифу этой клетки, т. е.  ;
;
2)
каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа
этой клетки, т. е. 
Доказанная теорема носит название теоремы
о потенциалах. На ней основан специальный метод решения ТЗ, названный методом
потенциалов.
Согласно
этой теореме, определение оптимальности плана проводится => образом:
1)
строкам и столбцам транспортной
таблицы приписываются потенциалы ui и vj, определенные как решение системы уравнений ui+ vj = сij для всех заполненных
клеток. Поскольку число уравнений m+n-1 на единицу
< числа неизвестных, один из потенциалов выбирается произвольным образом,
н-р, = 0, после чего однозначно определяются остальные потенциалы;
2)
для всех незаполненных клеток
находятся оценки sij = cij – ui+vj. Их экономический смысл: оценка cij показывает, как изменится стоимость перевозок при
загрузке этой клетки единицей ресурса. Если оценки всех пустых клеток
положительны, то найденный план является оптимальным, т.к. в этом случае
загрузка любой из пустых клеток вызовет увеличение стоимости перевозок. Если
все sij > 0, то полученный оптимальный план единственный.
В случае если хотя бы одна оценка sij = 0, оптимальных планов с одним и тем же значением
целевой ф-ции бесчисленное мн-во;
3)
если среди оценок есть
отрицательные, то план оптимальным не является и можно уменьшать стоимость
перевозок за счет заполнения клетки с отрицательной оценкой.
Перераспределение
поставок:
1)
выбирается клетка с отриц.
оценкой, если таких клеток несколько, то клетка, имеющая наименьшую оценку;
2)
для выбранной клетки строится
цикл, одна из вершин которого находится в этой клетке, а остальные в
заполненных клетках. Вершинам цикла поочередно приписываются знаки «+» и «–»,
начиная с пустой клетки. Знак «+» означает увеличение поставок в этой клетке,
«–» – уменьшение.
3)
для определения величины
перераспределенных поставок выбирается min-ое из
значений в клетках со знаком «–»;
4)
перераспределяя указанное кол-во
ресурсов по вершинам цикла, получаем новый опорный план;
5)
определяются новые потенциалы и
снова определяются критерии оптимальности.
11.Основные
понятия теории игр. Матричная игра с нулевой суммой. Минимаксные стратегии.
Цена игры, понятие седловой точки. Нахождение оптимального решения в чистых
стратегиях.
Теория
матричных игр представляет собой
теорию принятия решений в условиях неопределенности. Игра –
взаимодействие нескольких лиц, игроков, кот. направлено на достижение
нек. конеч. состояние, выигрыш, к которому стремиться каждый из игроков,
но не каждый может его получить. Стратегия – несколько вариантов
возможных действий, имеющихся у каждого игрока в распоряжении. Сделать ход
– выбрать одну из стратегий. Партия – последовательность ходов,
приводящих игру к конечному состоянию. По числу возможных стратегий игры
делятся на конечные и бесконечные. По числу участников - парная, когда игроков
2-е. Результаты такой игры в зависимости от выбора стратегии игроками могут
быть представлены с помощью платежной матрицы (матрица выигрышей)
размера m x n,
где m и n – число возможных стратегий 1-го и 2-го игроков
соответственно, а ее элементы аij представляют собой
выигрыш 1-го игрока при выборе им стратегии Аi при
условии, что 2-ой игрок выбрал стратегию Вj.
Матричная
игра с нулевой суммой – игра, в которой выигрыш одного игрока = проигрышу
другого.
Надо отметить важную терминологическую деталь:
стратегии, указываемые в приведенных примерах слева от платежной матрицы и над
ней, называются чистыми, каждый игрок применяет только одну из своих возможных
стратегий.
Каждый игрок выбирает для себя наиболее выгодную стратегию. При этом первый
игрок стремится выбрать такую стратегию, которая доставляет ему максимальный
выигрыш, тогда второй игрок выбирает стратегию, приводящую его к минимальному
проигрышу. В этой связи вводят понятия нижней и верхней чистой цены игры.
Нижней
чистой ценой игры (максимином)
называется число α, определяемое по формуле  .
.
Верхней
чистой ценой игры (минимаксом)
называется число β, определяемое по формуле  .
.
Стратегии
игроков, соответствующие максимину (минимаксу), называются максиминными
(минимаксными). Цена игры  -
оптимальное решение. Для любой матричной игры справедливы неравенства
-
оптимальное решение. Для любой матричной игры справедливы неравенства  и
и 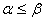 .
.
Если
 =
= 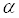 =
= 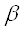 , то это чистая цена игры.
, то это чистая цена игры.
Седловая
точка платежной матрицы – элемент матрицы, = чистой цене игры. Чистая
стратегия игрока – стратегия, выбираемая им с вероятностью = 1. Если игра
имеет седловую точку, то соответствующие этой точке чистые стратегии будут
являться оптимальными для каждого из игроков. Если 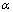 <
< , то оптимального решения в чистых стратегиях не
существует. Проверка платежной матрицы на
седловую (.)
, то оптимального решения в чистых стратегиях не
существует. Проверка платежной матрицы на
седловую (.)
–
в каждой строке находится
минимальный элемент, а среди них берется максимальный;
–
в каждом столбце находится
максимальный, а среди них берется минимальный;
–
если эти два элемента совпадают,
то матрица имеет седловую точку, в противном случае нет.
Седловая точка может быть не единственной. Для
пояснения рассмотрим пример.
12.Смешанные
стратегии. Доминирующие и доминируемые стратегии, упрощение матричной игры.
Сведение матричной игры к ЗЛП.
Если матричная игра не имеет седловой точки, то
решение игры затрудняется. В этих играх  .
Применение минимаксных стратегий в таких играх приводит к тому, что для
каждого из игроков выигрыш не превышает
.
Применение минимаксных стратегий в таких играх приводит к тому, что для
каждого из игроков выигрыш не превышает  , а
проигрыш - не меньше
, а
проигрыш - не меньше  . Для каждого игрока возникает
вопрос увеличения выигрыша (уменьшения проигрыша). Решение находят, применяя
смешанные стратегии.
. Для каждого игрока возникает
вопрос увеличения выигрыша (уменьшения проигрыша). Решение находят, применяя
смешанные стратегии.
Смешанной стратегией первого (второго) игрока называется вектор
р= , где
, где 
q= , где
, где 
Вектор p (q) означает вероятность применения i-й чистой
стратегии первым игроком (j-й чистой стратегии вторым игроком).
Поскольку игроки выбирают свои чистые
стратегии случайно и независимо друг от друга, игра имеет случайный характер и
случайной становится величина выигрыша (проигрыша). В таком случае средняя величина
выигрыша (проигрыша) - математическое ожидание - является функцией от
смешанных стратегий р, q:
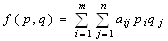 Функция f(p, q) называется платежной функцией игры.
Функция f(p, q) называется платежной функцией игры.
Стратегии р*= , q*=
, q*= называются оптимальными,
если для произвольных стратегий р=
называются оптимальными,
если для произвольных стратегий р= ,
q=
,
q= выполняется условие:
выполняется условие:
 (6.3)
(6.3)
Использование в игре оптимальных смешанных
стратегий обеспечивает первому игроку выигрыш, не меньший, чем при
использовании им любой другой стратегии р; второму игроку -
проигрыш, не больший, чем при использовании им любой другой стратегии q.
Совокупность оптимальных стратегий и цены
игры составляет решение игры.
Значение платежной функции при оптимальных
стратегиях определяет цену игры, т. е. 
Теорема 1. В смешанных стратегиях любая конечная матричная игра имеет седловую
точку.
Теорема 2. Для того чтобы смешанные стратегии р*= , q*=
, q*= были оптимальными
для игроков А и В в игре с матрицей
были оптимальными
для игроков А и В в игре с матрицей  и выигрышем v,
необходимо и достаточно выполнения неравенств:
и выигрышем v,
необходимо и достаточно выполнения неравенств:
 (6.4)
(6.4)
 (6.5)
(6.5)
Таким образом, для проверки того, что
набор (р*, q*, v) является
решением матричной игры, достаточно проверить, удовлетворяют ли р*,
q* неравенствам (6.4) и (6.5) и уравнениям


На основании данной теоремы
можно сделать вывод: если игрок А применяет оптимальную смешанную стратегию
р*, а игрок В - любую чистую стратегию, то выигрыш игрока А будет не
меньше цены. игры.
Аналогично: если игрок В
использует оптимальную смешанную стратегию q*, а игрок А - любую
чистую стратегию, то проигрыш игрока В не превысит цены игры.
Чистые стратегии игрока, входящие в его
оптимальную смешанную стратегию с вероятностями, отличными от нуля, называются
активными стратегиями игрока. Рассмотрим теорему об активных
стратегиях.
Теорема 3. Если один из игроков придерживается своей оптимальной
смешанной стратегии, то его выигрыш остается неизменным и равным цене игры
независимо от того, какую стратегию применяет другой игрок, если только тот не
выходит за пределы своих активных стратегий.
На основании данной теоремы
решение матричной игры можно упростить, выявив при этом доминирование одних
стратегий над другими. Так, рассматривая стратегии игрока А, сравниваем
соответствующие элементы строк s и t. Если все
элементы s-й строки не меньше элементов t-й
строки, то выигрыш игрока А при стратегии As
будет больше, чем при стратегии At. В этом случае стратегия As
доминирует над стратегией At. Стратегию As называют доминирующей, а стратегию At - доминируемой.
Аналогично, поскольку игрок В
заинтересован в минимизации проигрыша, доминирующим будет столбец с
наименьшими элементами.
Если в матричной игре имеем строки
(столбцы) с одними и теми же элементами, то строки (столбцы), а соответственно
и стратегии игроков А и В, называются дублирующими.
В матричной игре доминируемые и дублирующие строки (столбцы) можно
опускать, что не влияет на решение игры.
Теорема 4. Оптимальные смешанные стратегии р* и q*
соответственно игроков А и В в матричной игре  с
ценой v будут оптимальными и в матричной игре
с
ценой v будут оптимальными и в матричной игре  ценой v'=bv+c, где b>0.
ценой v'=bv+c, где b>0.
На
основании теоремы 6.5 платежную матрицу, имеющую отрицательные числа, можно
преобразовать в матрицу с положительными числами.
Приведение матричной игры к задаче линейного программирования
Пусть имеем игру размерности
 с матрицей
с матрицей

Обозначим через р*= , q*=
, q*=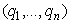 оптимальные
смешанные стратегии игроков А и В. Стратегия р*
игрока А гарантирует ему выигрыш не меньше v, независимо от выбора стратегии Вj игроком В.
Это можно записать так:
оптимальные
смешанные стратегии игроков А и В. Стратегия р*
игрока А гарантирует ему выигрыш не меньше v, независимо от выбора стратегии Вj игроком В.
Это можно записать так:
 (6.7)
(6.7)
где 
Аналогично стратегия q* игрока В гарантирует
ему проигрыш не больше v, независимо от выбора стратегии Аi игроком А,
т. е.
 (6.8)
(6.8)
где 
Поскольку элементы платежной матрицы на основании теоремы 6.5 всегда
можно сделать положительными, то и цена игры v > 0.
Преобразуем системы (6.7) и (6.8),
разделив обе части каждого неравенства на положительное число v, и введем новые обозначения

Получим:
 ,
где
,
где  (6.9)
(6.9)
 ,
где
,
где  6.10)
6.10)
Так как игрок А стремится
максимизировать цену игры v, то обратная
величина 1/v будет минимизироваться, поэтому оптимальная
стратегия игрока А определится из ЗЛП следующего вида: найти
минимальное значение функции  при ограничениях
(6.9).
при ограничениях
(6.9).
Оптимальная смешанная стратегия игрока В
определится решением задачи следующего вида: найти максимальное значение
функции  при ограничениях (6.10).
при ограничениях (6.10).
Алгоритм решения:
1.
если это необходимо, преобразуем
платежную матрицу игры, т.о. чтобы она не содерж. отриц. элементов

2.
составляем пару двойствен. Задач и
решаем из с-м
3.по найденным значения переменных ЗЛП опред цену игры

4.находим оптимальные вероятности

5.
6.ответ: 
13.Одномерная
минимизация: постановка задачи, понятие унимодальной функции. Принцип
минимизации унимодальных функций. Метод бисекций. Метод золотого сечения.
Пусть на множестве U Í R определена
функция f(x). Под минимизацией
функции f(x) на множестве U будем понимать решение следующей задачи:
найти хотя бы одну точку минимума x* и минимум f*=f(x*) этой функции на множестве U.
Задача нахождения точки максимума и
максимального значения функции f(x) сводится к задаче минимизации
заменой f(x) на -f(x), поэтому ниже будут рассматриваться только
задачи на минимизацию.
Существование локальных
минимумов функции f(х), отличных от абсолютного, почти всегда
затрудняет поиск точек x*ÎU*, поэтому многие приближенные методы минимизации
применимы только тогда, когда любой локальный минимум f(х) является
одновременно и глобальным. Один из классов функций, удовлетворяющих этому
условию, составляют унимодальные функции.
Функция f(х) называется унимодальной
на отрезке [а; b], если она непрерывна на [а; b]
и существуют числа α и β,  такие, что;
такие, что;
1)
если α < а, то на отрезке [а; α ] f (х)
монотонно убывает;
2)
если β < b, то на
отрезке [β; b] f (x) монотонно возрастает;
3)
при хÎ[α; β] 
Множество функций, унимодальных на отрезке
[а; b], будем обозначать Q[а; b].
Для проверки унимодальности функции f(х)
на практике обычно используют следующие критерии:
1) если
функция f(х) дифференцируема на отрезке [а; b]
и производная f'(х) не убывает на этом отрезке, то f(x)Î Q[а; b].
2) если
функция f(x) дважды дифференцируема на отрезке [а; b] и f”(х)³0 при xÎ[а;
b], то f(x)Î Q[а; b].
Метод деления отрезка пополам является простейшим последовательным методом
минимизации. Он позволяет для любой функции f(x)Î Q[а; b] построить
последовательность вложенных отрезков  ,
каждый из которых содержит хотя бы одну из точек минимума х*
функции f(х) Пусть e>0 - требуемая точность определения точки х*. Выбрав
,
каждый из которых содержит хотя бы одну из точек минимума х*
функции f(х) Пусть e>0 - требуемая точность определения точки х*. Выбрав  , построим последовательности
, построим последовательности 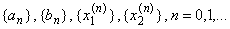 , используя рекуррентные формулы:
, используя рекуррентные формулы:

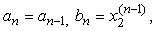 если
если  (1.1)
(1.1)
 если
если 
Полагая  ,
находим х* с абсолютной погрешностью, не превосходящей величины
,
находим х* с абсолютной погрешностью, не превосходящей величины 
ПОЯСНЕНИЯ Рассмотрим [a,b],
на концах кот. выполн. условие f(a)*f(b)<0. Разделим отр пополам и выберем тот, кот
удовлетворяет начальному условию. Не примен. для отыск. Корней четной кратности
и плохо примен. Для нечет кратности больше 1.
Метод золотого сечения также является последовательным методом минимизации.
Деление отрезка на две неравные части так, что отношение длины всего отрезка к
длине большей его части равно отношению длины большей части к длине меньшей части,
называется золотым сечением этого отрезка.
Золотое сечение отрезка [а; b]
осуществляется двумя точками:

причем x1 есть вторая точка золотого сечения отрезка [а;
х2]. а х2 - первая точка золотого
сечения отрезка [х1; b].
Зная одну из точек золотого сечения
отрезка [а; b], другую можно найти по одной из формул
 (1.2)
(1.2)
Пусть f(x)Î Q[а; b] и
требуется найти точку минимума функции f(х) на [а; b].
Построим последовательности  , следующим образом:
, следующим образом:
 , если
, если  (1.3)
(1.3)
 если
если 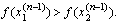
где 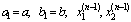 -
первая и вторая точки золотого сечения отрезка
-
первая и вторая точки золотого сечения отрезка 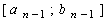 .
.
Для определения чисел  по найденным
по найденным 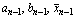 необходимо
выполнить следующие операции:
необходимо
выполнить следующие операции:
1)
найти одну из точек золотого сечения отрезка  по известной другой точке
по известной другой точке
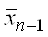 , используя формулы (1.2);
, используя формулы (1.2);
2)
вычислить значение f(х) во вновь найденной точке золотого сечения
(значение в другой точке 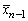 уже вычислено на
одном из предыдущих шагов);
уже вычислено на
одном из предыдущих шагов);
3)
сравнить значения  и
и  и
найти
и
найти  по формулам
(1.3).
по формулам
(1.3).
Таким образом, на каждом шаге определения  требуется вычисление одного значения f(х).
Положив
требуется вычисление одного значения f(х).
Положив  , найдем точку минимума х* с
точностью
, найдем точку минимума х* с
точностью  :
:

14.Условие
Липшица. Минимизация функций, удовлетворяющих условию Липшица
Метод ломаных является последовательным методом, рассчитанным на
минимизацию произвольных (не обязательно унимодальных) функций, удовлетворяющих
условию Липшица. Говорят, что функция f(х) удовлетворяет на отрезке [а; b]
условию Липшица, если существует такое число L > 0 (константа
Липшица), что
\f(x')-f(x")\<L\x'-x"\ (1.5)
для всех х', х" Î [а; b].
Для проверки условия Липшица на практике
используют следующий факт: если функция f(х) имеет на отрезке [а;
b] ограниченную производную, то она удовлетворяет
условию (1.5), где  .
.
Пусть функция f(х) удовлетворяет на
[а; b] условию Липшица с константой L. Опишем
метод ломаных для минимизации f(х).
Положим

и реализуем следующую схему вычислений:
Шаг 1. Вместо пары чисел  образуем две новые
пары
образуем две новые
пары  и
и  следующим
образом:
следующим
образом:
 где
где
 .
.
Шаг 2. Из полученных двух пар  и
и  выберем ту, у которой вторая компонента
минимальна. Обозначим ее
выберем ту, у которой вторая компонента
минимальна. Обозначим ее  и исключим из
рассматриваемого множества (очевидно, на данном шаге в качестве
и исключим из
рассматриваемого множества (очевидно, на данном шаге в качестве  можно взять любую из пар
можно взять любую из пар  ,
,  ).
Вместо пары
).
Вместо пары  добавляем две новые пары
добавляем две новые пары  и
и  ,
компоненты которых находятся по формулам
,
компоненты которых находятся по формулам
 где
где
 .
.
В результате получим множество, состоящее
из трех пар чисел (х, р).
Шаг п. Из п
полученных на предыдущих шагах пар (х, р) выбираем ту, у
которой вторая компонента р минимальна. Обозначим ее  . Исключаем эту пару из рассматриваемого
множества и добавляем вместо нее две новые пары чисел
. Исключаем эту пару из рассматриваемого
множества и добавляем вместо нее две новые пары чисел 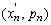 и
и
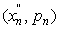 по формулам
по формулам
 где
где
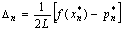 . (1.6)
. (1.6)
Полагая х* ≈ , f*
≈ f(
, f*
≈ f( ), получим приближенное решение
задачи минимизации. Точность определения f*
характеризуется неравенствами
), получим приближенное решение
задачи минимизации. Точность определения f*
характеризуется неравенствами  .
.
Геометрически метод ломаных состоит в построении
последовательности ломаных, приближающихся к графику функции f(х) снизу
и имеющих угловые коэффициенты всех звеньев, равные ±L

15.Методы
минимизации функций одной переменной, основанные на вычислении производных
функции: метод касательных, метод Ньютона.
Mетод
касательных применяется для минимизации выпуклых дифференцируемых функций.
Функция f (х) называется выпуклой на отрезке [а; b], если
 (1.7)
(1.7)
для
произвольных х', х"Î [а; b] и .
.
Проверка
условия (7) почти всегда вызывает затруднения, поэтому на практике используют
следующий критерий выпуклости:
Для
того, чтобы дважды дифференцируемая на отрезке [а; b] функция f(х) была
выпуклой на отрезке [а; b], необходимо и достаточно, чтобы f"[x)≥0
при всех хÎ[а; b].
Опишем
метод касательных. Пусть f(х) - выпуклая дифференцируемая на отрезке [а; b]
функция, причем  . Построим последовательности
. Построим последовательности  , в соответствии с
рекуррентными соотношениями
, в соответствии с
рекуррентными соотношениями

 , (1.8)
, (1.8)
 при
при  , (1.9)
, (1.9)
 при
при  .
.
После
п шагов полагаем  . Требуемая точность минимизации f(x)
считается достигнутой, если производная f'(c) достаточно близка к нулю, т. е. |
f'(cп)| £ e, где e>0 - заданное число, характеризующее точность.
. Требуемая точность минимизации f(x)
считается достигнутой, если производная f'(c) достаточно близка к нулю, т. е. |
f'(cп)| £ e, где e>0 - заданное число, характеризующее точность.
Метод
касательных имеет простой геометрический смысл: величина сn-1 из (1.8) - это
абсцисса точки пересечения касательных к графику f(x), проведенных в граничных
точках отрезка 
Если
условие  не
выполняется, то
не
выполняется, то
а)
х*=а при f’ (а) > 0, f’ (b) > 0;
б)
х*=b при f’ (а) < 0, f’ (b) < 0;
в)
х*=а, если f'(a)=0, и х*=b, если f’(b)=0.
Метод
Ньютона, использующий не только первую, но и вторую производные функции f(x),
при определенных условиях обеспечивает значительно более высокую, чем
рассмотренные выше методы минимизации, скорость сходимости к точке минимума х*.
Пусть
f(x) - выпуклая дважды дифференцируемая на R функция. Выбрав начальное
приближение х0, построим последовательность
 (1.10)
(1.10)
Считая
неравенство | f'(хп)| £ e (e - достаточно
малое число) условием достижения требуемой точности вычислений, положим х*
≈xn, f* ≈ f(xn).
Оценка
скорости сходимости может быть сформулирована следующим образом. Пусть f(x) -
дважды дифференцируемая на R функция, причем  при всех xÎ R. и f"'(х) удовлетворяет условию Липшица на R
с константой L. Тогда, если начальное приближение х0 удовлетворяет условию
при всех xÎ R. и f"'(х) удовлетворяет условию Липшица на R
с константой L. Тогда, если начальное приближение х0 удовлетворяет условию  , то
последовательность (1.10) сходится к единственной точке минимума х* функции
f(х) на R, причем
, то
последовательность (1.10) сходится к единственной точке минимума х* функции
f(х) на R, причем 
16.Постановка
задачи минимизации функции многих переменных. Выпуклые множества и выпуклые
функции. Квадратичные функции, их представление в матричной форме.
Пусть Еп - п-мерное
евклидово пространство арифметических векторов  .
Множество U Ì Еп
называется выпуклым, если вместе с любыми двумя точками
.
Множество U Ì Еп
называется выпуклым, если вместе с любыми двумя точками  оно содержит и отрезок, соединяющий эти
точки, т. е.
оно содержит и отрезок, соединяющий эти
точки, т. е.
 для всех
для всех  (2.1)
(2.1)
Функция f(x), заданная на выпуклом множестве U, называется выпуклой
на этом множестве, если для любых точек  и
произвольного числа
и
произвольного числа  справедливо неравенство
справедливо неравенство
 (2.2)
(2.2)
На практике обычно используют следующий
критерий выпуклости функции:
Если f(х) -
дважды дифференцируемая на выпуклом множестве U функция и матрица ее вторых
производных  (гессиан) положительно
определена при всех xÎU,
то функция f(х) является выпуклой на множестве U.
(гессиан) положительно
определена при всех xÎU,
то функция f(х) является выпуклой на множестве U.
это утверждение можно сформулировать в более удобном
для проверки виде:
Если все угловые
миноры матрицы, f"(х) положительны при хÎU, то
функция f(х) выпукла на множестве U.
Во многих задачах
оптимизации рассматриваются квадратичные функции, т. е. функции вида 
Если положить  то
получим симметрическую матрицу
то
получим симметрическую матрицу  , с помощью которой
можно представить квадратичную функцию в виде
, с помощью которой
можно представить квадратичную функцию в виде
 (2.3)
(2.3)
где  ,
,  - векторы-столбцы.
- векторы-столбцы.
Градиент и матрица вторых производных
функции (2.3) равны
 .
.
Таким образом, для того чтобы функция
(2.3) была выпуклой, достаточно, чтобы матрица Q была
положительно определена.
17.Градиентные
методы безусловной минимизации: дробление шага и наискорейший спуск. Эффект
оврагов, методы его устранения. Метод сопряженных направлений.
Градиент скалярной функции f(x)
в некоторой точке xk направлен в сторону наискорейшего возрастания функции
и ортогонален линии уровня (поверхности постоянного значения функции f(x), проходящей через точку xk).
Вектор, противоположный градиенту f’(xk,), антиградиент,
направлен в сторону наискорейшего убывания функции f(x). Выбирая в качестве направления спуска pk антиградиент функции f(x) в точке xk, мы
приходим к итерационному процессу вида
 (2.4)
(2.4)
В координатной форме этот процесс
записывается следующим образом:

где величины  (параметрические
шаги) выбираются достаточно малыми для того, чтобы выполнялось условие:
(параметрические
шаги) выбираются достаточно малыми для того, чтобы выполнялось условие:
 (2.12)
(2.12)
В качестве условия окончания вычислений
обычно используется близость к нулю градиента  т.
е. выполнение неравенств
т.
е. выполнение неравенств
 или
или  ,
,
где e - заданное достаточно малое
число, после чего полагают  .
.
Дробление шага. Пусть f(х) - выпуклая дифференцируемая во
всем пространстве Еп функция и требуется найти ее точку
минимума х*. Выбрав произвольное начальное приближение 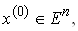 построим последовательность
построим последовательность
 (2.11)
(2.11)
проверяем выполнилось ли условие:
 (2.12)
(2.12)
Если условие выполняется, то это новая
(.). Если при некотором k условие (2.12) нарушается, то шаг  в (2.11) уменьшают (дробят) в заданное
число раз до выполнения неравенства (2.12) и продолжают вычисления.
в (2.11) уменьшают (дробят) в заданное
число раз до выполнения неравенства (2.12) и продолжают вычисления.
Наискорейший спуск.
Процесс, на каждой итерации которого шаг αk выбирается
из условия минимума функции f(x) в направлении
движения, т. е.
 (2.15)
(2.15)
называется методом наискорейшего спуска. В этом варианте
градиентного спуска на каждой итерации требуется решать задачу одномерной
минимизации (2.15).
Шаг α выбирается из условия
минимизации по α функции
 ,
,
и поэтому
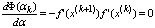 .
.
Таким
образом, направления спуска на двух последовательных итерациях взаимно
ортогональны.
Пояснение: Находим  , найденные
, найденные  подставляем
в исходную функцию и полученное Ур-ние решаем на min. Если f(x) - квадратичная функция (2.3), то величина αk может быть найдена в явном виде
подставляем
в исходную функцию и полученное Ур-ние решаем на min. Если f(x) - квадратичная функция (2.3), то величина αk может быть найдена в явном виде
 (2.16)
(2.16)
Таким образом, для квадратичной функций
метод наискорейшего спуска состоит в построении последовательности  по формулам (2.14), (2.16).
по формулам (2.14), (2.16).
Овраги.
Градиентные методы сходятся со скоростью геометрической прогрессии со
знаменателем  , зависящим от М и т
- равномерных по х оценок сверху и снизу соответственно
максимального и минимального собственных чисел матрицы f’’(х). Если М и т мало отличаются друг от
друга - матрица f(х) хорошо
обусловлена, - то число q мало и, следовательно, сходимость методов
достаточно высокая. Если же
, зависящим от М и т
- равномерных по х оценок сверху и снизу соответственно
максимального и минимального собственных чисел матрицы f’’(х). Если М и т мало отличаются друг от
друга - матрица f(х) хорошо
обусловлена, - то число q мало и, следовательно, сходимость методов
достаточно высокая. Если же  , то q
близко к единице, и градиентные методы начинают сходиться плохо. Этот факт
хорошо интерпретируется геометрически и известен в литературе как «эффект
оврагов». Если числа М и т сильно отличаются, то топография
поверхностей уровня f(x)=const имеет овражную
структуру.
, то q
близко к единице, и градиентные методы начинают сходиться плохо. Этот факт
хорошо интерпретируется геометрически и известен в литературе как «эффект
оврагов». Если числа М и т сильно отличаются, то топография
поверхностей уровня f(x)=const имеет овражную
структуру.
Траектория градиентного метода
характеризуется довольно быстрым спуском на «дно» оврага и затем медленным
зигзагообразным движением в точку минимума
Одним из выходов в создавшейся ситуации
является изменение масштабов независимых переменных целевой функции. Поясним
этот способ на следующем примере.
Пусть функция f(х) имеет вид
 ,
(2.17)
,
(2.17)
где величины  >0
сильно различаются между собой. Поверхности уровней функции (2.17) вытянуты
вдоль тех осей
>0
сильно различаются между собой. Поверхности уровней функции (2.17) вытянуты
вдоль тех осей 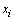 , которым соответствуют
малые
, которым соответствуют
малые  . Заменой переменных
. Заменой переменных

можно добиться того, чтобы в новых переменных  линии уровня стали сферами. Для этого
достаточно принять
линии уровня стали сферами. Для этого
достаточно принять
 .
.
Тогда получим преобразование
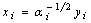 .
(2.18)
.
(2.18)
В случае, когда f(х) не
квадратичная, а достаточно гладкая функция общего вида, выбирают
 (2.19)
(2.19)
в точке х одномерного минимума вдоль
направления  . Множитель
. Множитель 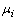 пропорционален радиусу кривизны линии
уровня в точке х. Преобразование (2.19) конечно не превратит
поверхностей уровня в сферы, но в некоторых случаях уменьшит их вытянутость.
пропорционален радиусу кривизны линии
уровня в точке х. Преобразование (2.19) конечно не превратит
поверхностей уровня в сферы, но в некоторых случаях уменьшит их вытянутость.
Масштабирование переменных в общем случае
приводит к итерационному процессу вида
 (2.20)
(2.20)
где матрица Вk
зависит от номера итерации.
Методы вида (2.20) часто называют
релаксационными. При Bk = Е имеем
обычный градиентный метод (2.4).
Сопряженные
направления. Два вектора х
и у в пространстве Еп называются Н-сопряженными
(или сопряженными по отношению к матрице Н) или Н-ортогональными, если (х,
Ну)=0.
Сопряженность можно считать обобщением
понятия ортогональности. В самом деле, когда Н=Е, векторы х и у
ортогональны.
Квадратичная функция п переменных
может быть минимизирована за п (или менее) шагов, если эти шаги предпринимать
в сопряженных направлениях.
Пусть  -
произвольная начальная точка, a
-
произвольная начальная точка, a  - произвольное начальное направление
поиска. Тогда следующую точку
- произвольное начальное направление
поиска. Тогда следующую точку  определим по формуле
определим по формуле
 (2.21)
(2.21)
в которой длину шага  вычислим
из условия минимума функции f(x) по l в направлении движения, т. е. из условия
вычислим
из условия минимума функции f(x) по l в направлении движения, т. е. из условия
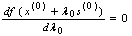 (2.22)
(2.22)
Возьмем в качестве  точку
с координатами (1, 1), а в качестве
точку
с координатами (1, 1), а в качестве  - вектор {1, 2}.
(Здесь вектор
- вектор {1, 2}.
(Здесь вектор  в иллюстративных целях взят
произвольным, хотя можно было бы начать движение из точки
в иллюстративных целях взят
произвольным, хотя можно было бы начать движение из точки  по антиградиенту функции f(x).) Координаты точки
по антиградиенту функции f(x).) Координаты точки  в
соответствии с формулой (2.21) равны
в
соответствии с формулой (2.21) равны

Для вычисления длины шага, согласно
(2.22), получим уравнение

Выберем теперь направление  , движения из точки
, движения из точки  сопряженным к
сопряженным к  относительно
матрицы вторых производных целевой функции, т. е. из условия
относительно
матрицы вторых производных целевой функции, т. е. из условия

18.Относительный
экстремум, метод исключения переменных. Метод множителей Лагранжа. Теорема
Куна-Таккера.
Относительный экстремум.
Метод исключения. Рассмотрим задачу на относительный экстремум. Решение
задачи об отыскании экстремумов функции п переменных f(x) на всем пространстве Еп, может быть
сведено с помощью необходимых условий к решению системы уравнений
 ,
,
в результате чего определяются стационарные точки
функции f(x). Это
возможно и для задачи отыскания экстремумов функции f(x) при наличии ограничений типа равенств
 -уравнения связи
-уравнения связи
Точка х*, удовлетворяющая этим
условиям явл-ся допустимой.
Допустимая точка х* доставляет относительный
локальный минимум функции f(х), если можно указать такое число e >0, что для всех х, удовлетворяющих уравнениям связи и
условию  , имеет место неравенство
, имеет место неравенство
f(x) > f(x*).
Метод
Лагранжа
Поскольку в точке х*,
доставляющей безусловный экстремум функции, ее полный дифференциал равен нулю,
т. е.
 (*)
(*)
где  -
дифференциалы «зависимых» переменных,
-
дифференциалы «зависимых» переменных,  -
дифференциалами «независимых» переменных.
При дифференцировании полным образом уравнений связи, получим что дифференциалы «зависимых» переменных с дифференциалами
«независимых» следующим образом:
-
дифференциалами «независимых» переменных.
При дифференцировании полным образом уравнений связи, получим что дифференциалы «зависимых» переменных с дифференциалами
«независимых» следующим образом:
 , (**)
, (**)
Исключим теперь дифференциалы
«зависимых» переменных из уравнений (*) и (**), для этого умножим каждое из
уравнений системы (**) на произвольные множители  и
результаты сложим с уравнением (*), тогда получим следующее равенство:
и
результаты сложим с уравнением (*), тогда получим следующее равенство:
 (***)
(***)
Распорядимся множителями  таким образом, чтобы обратились в нуль
коэффициенты при дифференциалах «зависимых» переменных, т. е.
таким образом, чтобы обратились в нуль
коэффициенты при дифференциалах «зависимых» переменных, т. е.
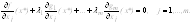
Уравнений относительно множителей  , которая имеет единственное решение
Так как по условию определитель
, которая имеет единственное решение
Так как по условию определитель 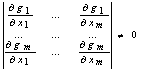 .
При выбранных таким образом значениях множителей в равенстве (***) останутся
только члены, содержащие дифференциалы «независимых» переменных. Поэтому
коэффициенты при этих дифференциалах должны быть нулями, т. е.
.
При выбранных таким образом значениях множителей в равенстве (***) останутся
только члены, содержащие дифференциалы «независимых» переменных. Поэтому
коэффициенты при этих дифференциалах должны быть нулями, т. е.
 (4.8)
(4.8)
Таким образом, мы получили
систему п+т уравнений (4.1), (4.7), (4.8) относительно п+т
неизвестных  ,
, . Этот результат представляет собой основное
содержание метода множителей Лагранжа и позволяет определить множество
«претендентов» на решение в задаче на относительный экстремум.
. Этот результат представляет собой основное
содержание метода множителей Лагранжа и позволяет определить множество
«претендентов» на решение в задаче на относительный экстремум.
Метод Лагранжа состоит из следующих этапов:
1) составляется функция п+т
переменных, которая называется функцией Лагранжа:
 ;
;
2)
вычисляются и приравниваются нулю ее частные производные по х и l:

3)
Составленная система п+т уравнений решается относительно п+т
неизвестных  ,
, .
.
Эта система уравнений представляет собой
необходимые условия первого порядка в задаче на относительный экстремум, а ее
решения  принято называть условно-стационарными
точками.
принято называть условно-стационарными
точками.
Теорема (Куна—Таккера). Предположим,
что существует вектор  такой, что
такой, что
 . Тогда необходимым и достаточным
условием оптимальности вектора х*, принадлежащего допустимой
области, является существование такого вектора l*, что для всех
. Тогда необходимым и достаточным
условием оптимальности вектора х*, принадлежащего допустимой
области, является существование такого вектора l*, что для всех
 и
и  имеет
место неравенство
имеет
место неравенство  .
.
Если функции f(х) и  являются
дифференцируемыми, то неравенства
являются
дифференцируемыми, то неравенства 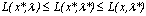 ,
где
,
где 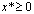 ,
,  эквивалентны
следующим «локальным» условиям Куна-Таккера:
эквивалентны
следующим «локальным» условиям Куна-Таккера:




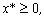

19.Постановка
задачи дробно-линейного программирования. Сведение задачи дробно-линейного
программирования к ЗЛП.
Целевая функция
представляется в виде частного двух линейных функций.

 Предположим, что в допустимой области
знаменатель не обращается в 0, т.е. f(x) определена на
всей области. Тогда можно считать, что знаменатель на всей допустимой области
Предположим, что в допустимой области
знаменатель не обращается в 0, т.е. f(x) определена на
всей области. Тогда можно считать, что знаменатель на всей допустимой области  . Данная задача может быть сведена к ЗЛП
с помощью замены переменных.
. Данная задача может быть сведена к ЗЛП
с помощью замены переменных. 
 ,
заменим
,
заменим 
Тогда ограничения будут иметь
вид: 
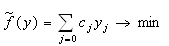

y0 должна
быть обязательно базисной, т.к. y0>0.
Предположим, что найдено
оптимальное решение (y0*, y1*,.., yn*)  , тогда в силу сделанных замен найдем:
, тогда в силу сделанных замен найдем:
xj*= yj*/ y0* ; f*(x)= 
20.Квадратичное
программирование: постановка задачи. Применение метода искусственного базиса
для нахождения оптимального решения задачи квадратичного программирования.
Квадратичные функция – это функция вида  или
в матричной форме f(x)=1/2 (Qx, x)+(r,x)
или
в матричной форме f(x)=1/2 (Qx, x)+(r,x)
Пусть имеется выпуклая
квадратичная целевая функция
f(x)=1/2 (Qx, x)+(r,x) min
min

Тогда задачу кв. прог-ния м.
сформулировать => образом: найти min выпуклой кв. ф-ции при
ограничениях им. вид линейных нер-в
Составим функцию Лагранжа F(x, λ)
f(x)=1/2 





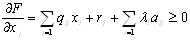 ;
; 
Перейдем к каноническому
виду, тогда локальные условий К-Т принимут => вид
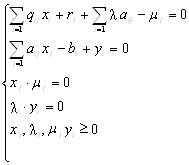
поэтому
для решения полученной системы сожжет быть использован метод искусственного
базиса со следующим ограничением на столбец переводимый в базисные переменные –
переводить 2 связные переменные в базисные одновременно нельзя. Если среди
ограничений имеются ограничения типа = их необходимо заменить на 2 ограничения
типа неравенства.
21.Метод
возможных направлений для задачи нелинейного программирования с линейными
ограничениями. Выбор возможного направления(ВН), определение величины шага.
Рассмотрим метод возможных направлений решения задачи
минимизации выпуклой дифференцируемой нелинейной функции f(х) на допустимом множестве U, заданном линейными
ограничениями

 (*)
(*)  (**)
(**)
Выбор возможного направления. Опишем
выбор вектора  из
из  (***),
определяющего возможное направление убывания функции f(х) в точке
(***),
определяющего возможное направление убывания функции f(х) в точке 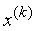 . Рассмотрим
возможные случаи.
. Рассмотрим
возможные случаи.
1. Пусть в точке  все
неравенства
все
неравенства  и
и
 выполняются как строгие. Это означает, что
выполняются как строгие. Это означает, что  - внутренняя точка допустимого
множества U. Тогда
- внутренняя точка допустимого
множества U. Тогда

2. Пусть хотя бы одно из неравенств (*), (**) в точке  обращается в равенство, т.е.
обращается в равенство, т.е. 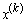 является граничной точкой допустимого
множества U. Тогда выбор
является граничной точкой допустимого
множества U. Тогда выбор  в соответствии с
в соответствии с  , вообще говоря, невозможен, так как
может оказаться, что точка
, вообще говоря, невозможен, так как
может оказаться, что точка  из (***) при
любом
из (***) при
любом  > 0 не принадлежит множеству U.
> 0 не принадлежит множеству U.
Опишем, как определять возможное направление убывания 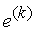 в этом случае.
в этом случае.
Обозначим через  и
и
 множества индексов, соответствующих
ограничениям (*) и (**), которые в точке
множества индексов, соответствующих
ограничениям (*) и (**), которые в точке  обращаются
в равенства, т. е.
обращаются
в равенства, т. е.

Представим компоненты  вектора
вектора
 для
для  в
виде
в
виде
 ,
,
где
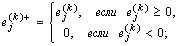

Очевидно,  и
и  для всех
для всех  .
.
Такое представление для  ,
,  , позволяет находить вектор
, позволяет находить вектор  как решение задачи линейного
программирования, содержащей условие неотрицательности переменных, несмотря на
то, что его компоненты могут быть отрицательными.
как решение задачи линейного
программирования, содержащей условие неотрицательности переменных, несмотря на
то, что его компоненты могут быть отрицательными.
Для  представление
представление  не используется, так как у вектора
не используется, так как у вектора  , определяющего возможное направление,
компоненты
, определяющего возможное направление,
компоненты  с номерами
с номерами  не могут быть отрицательными.
не могут быть отрицательными.
Т.к. вектор ВН д. максимально совпадать с –grad
, то угол между  и grad
д.б. max. т.е.
и grad
д.б. max. т.е.  , но т.к. мы
находимся в граничной точке, то направление не д.б. направлено из ОДЗ, поэтому
угол между
, но т.к. мы
находимся в граничной точке, то направление не д.б. направлено из ОДЗ, поэтому
угол между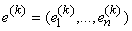 и внешней нормалью к границе д.б. ≥90, поэтому
вектор
и внешней нормалью к границе д.б. ≥90, поэтому
вектор  из
из  ищется как решение следующей задачи
линейного программирования:
ищется как решение следующей задачи
линейного программирования:
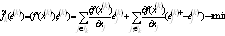
 где
где  внешняя нормаль к границе
внешняя нормаль к границе
Также должно выполняться условие
нормировки , которое является ограничением на
длину вектора
, которое является ограничением на
длину вектора  и обеспечивает ограниченность
снизу целевой функции
и обеспечивает ограниченность
снизу целевой функции
 ,
, 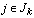 , гарантирует, что направление искомого вектора
, гарантирует, что направление искомого вектора  является возможным по отношению к j-му ограничению
является возможным по отношению к j-му ограничению  исходной задачи
исходной задачи
 ,
,  ,
,
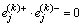 ,
,  ,где
,где  .
.
Для учета дополнительного последнего условия при
решении задачи симплекс-методом следует не включать переменные  и
и  с
одинаковым номером j в число базисных одновременно.
с
одинаковым номером j в число базисных одновременно.
Соотношения  ,
,  , и
, и  ,
, 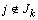 , следуют из представления
, следуют из представления  компонент
компонент  ,
,  , вектора
, вектора  .
.
Нахождение максимально допустимого перемещения. Величину перемещения  вдоль
направления
вдоль
направления  д. обеспечивать max
убывание функции, поэтому для найденного вектора
д. обеспечивать max
убывание функции, поэтому для найденного вектора  величину
шага найдем из условия:
величину
шага найдем из условия:
где
минимум берется по всем  таким, что
таким, что  , т.е.
, т.е.
 (****)
(****)
где
 и
и  -
максимальные перемещения, при которых для точки
-
максимальные перемещения, при которых для точки  из
из  выполняются соответственно i-e
ограничение
выполняются соответственно i-e
ограничение  и
j-е ограничение
и
j-е ограничение  ,т. е.
,т. е.


а  находится из условия наискорейшего
спуска вдоль направления вектора
находится из условия наискорейшего
спуска вдоль направления вектора  без учета ограничений
без учета ограничений
 ,
,  ,
т. е.
,
т. е.
 ,
где
,
где 
Другими словами при выбранном
направлении выбираемый шаг не должен нарушать ограничения, т.е. мы д. шагнуть
за границы области для этого необходимо определить расстояние до всех границ в
направлении которых мы движемся, т.е.  >0(угол
между внешней нормалью границы и вектором направлений острый), и для шага
выбрать min из этих
расстояний.
>0(угол
между внешней нормалью границы и вектором направлений острый), и для шага
выбрать min из этих
расстояний.
Приведем описание k-го шага
решения задачи  при
ограничениях (*), (**) методом возможных направлений.
при
ограничениях (*), (**) методом возможных направлений.
1. Подставить  в
неравенства (*) и (**) и определить множества индексов
в
неравенства (*) и (**) и определить множества индексов  и
и  по
формулам
по
формулам 
2. Если  =
= =Æ, найти вектор
=Æ, найти вектор
 из
из  в
противном случае определить
в
противном случае определить  из решения задачи
линейного программирования
из решения задачи
линейного программирования  с
помощью формулы
с
помощью формулы  .
.
3. Для найденного вектора 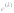 определить
максимально допустимое перемещение
определить
максимально допустимое перемещение
4. Найти очередное приближение  по
формуле
по
формуле 
При выполнении хотя бы одного из условий  или
или 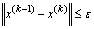 ,
где e > 0 - число, определяющее точность решения
задачи, вычисления завершают, полагая
,
где e > 0 - число, определяющее точность решения
задачи, вычисления завершают, полагая 
Любое из равенств 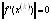 ,
, 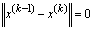 означает,
что точка минимума х* функции f(х) на множестве U найдена
точно:
означает,
что точка минимума х* функции f(х) на множестве U найдена
точно: 
22.Методы
штрафных и барьерных функций.
Основная идея метода заключается в том, что от задачи
условной минимизации мы переходим к задаче безусловной минимизации. Это
достигается за счет того что, функция безусловной минимизации строится таким
образом, чтобы внутри ОДЗ она совпадала с исходной функцией, а вне области
неограниченно возрастала. Рассмотрим задачу отыскания минимума функции f(х) на некотором множестве W. Формально она
эквивалентна задаче безусловной минимизации суммы
 ,
,
где
 - так называемая индикаторная
функция:
- так называемая индикаторная
функция:
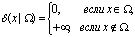
Когда множество W задано
ограничениями типа равенств и неравенств, используя фигурирующие в них функции,
совсем нетрудно строить вполне конкретные «штрафы»  такие,
что при всех
такие,
что при всех 
 .
.
Тогда задача, эквивалентная исходной, записывается
так:
 .
.
Если операции взятия минимума и предела при этом
окажутся перестановочными, мы получим последовательность обычных задач
безусловной минимизации вида
 ,
,
пределом
решений которых при k®¥ будет точка минимума функции f(х) на множестве
W.
Существуют два подхода к построению штрафов  : - методы внутренней точки (методы
внутренних штрафных или, как их еще называют, барьерных функций) и методы
внешней точки (внешних штрафных функций).
: - методы внутренней точки (методы
внутренних штрафных или, как их еще называют, барьерных функций) и методы
внешней точки (внешних штрафных функций).
Методы внутренних штрафных
(барьерных) функций
Когда множество W задано с помощью
непрерывных функций  ,
ограничениями-неравенствами
,
ограничениями-неравенствами

причем существуют точки, в которых  построим последовательность штрафов
построим последовательность штрафов  , сходящихся при определенных
предположениях к индикаторной функции и неограниченно возрастающих приближении х
к границе W
, сходящихся при определенных
предположениях к индикаторной функции и неограниченно возрастающих приближении х
к границе W
|
В
данном случае поиск минимума штрафной функции

нужно
начинать с точки, в которой все ограничения исходной задачи выполнены как
строгие неравенства.
При
разумной организации этого поиска последние будут автоматически сохраняться
и в дальнейшем: выход на границу W, где штраф 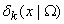 бесконечен, при минимизации суммы бесконечен, при минимизации суммы  смысла не имеет. Таким образом,
процесс движения к минимуму функции смысла не имеет. Таким образом,
процесс движения к минимуму функции  никогда
не покинет множества W. Отсюда и название – «методы внутренней точки». никогда
не покинет множества W. Отсюда и название – «методы внутренней точки».
|
Рис. 8.1.
|
 Дадим следующее определение. Пусть множество
Дадим следующее определение. Пусть множество  задано. Последовательность функций
задано. Последовательность функций  , определенных во всех внутренних точках
множества W, называется
последовательностью барьерных функций этого множества, если выполняются
условия:
, определенных во всех внутренних точках
множества W, называется
последовательностью барьерных функций этого множества, если выполняются
условия:
1.  для любой
фиксированной внутренней точки х множества W;
для любой
фиксированной внутренней точки х множества W;
2.  для любой
последовательности
для любой
последовательности 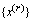 внутренних точек
множества W, сходящейся
к какой-либо граничной точке этого множества.
внутренних точек
множества W, сходящейся
к какой-либо граничной точке этого множества.
Чаще всего в качестве штрафов рассматриваемого типа
для задач
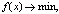 (*) при
ограничениях
(*) при
ограничениях 
используют
такие функции:
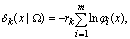 (**) или
(**) или  (***)
(***)
Здесь
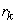 - положительное число, называемое
параметром штрафа. Важно отметить, что если
- положительное число, называемое
параметром штрафа. Важно отметить, что если 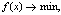 -
задача выпуклого программирования, т. е.
-
задача выпуклого программирования, т. е.  -
вогнутые функции, то оба предлагаемых штрафа выпуклы. Соотношение
-
вогнутые функции, то оба предлагаемых штрафа выпуклы. Соотношение  и для того, и для другого выполняется,
если
и для того, и для другого выполняется,
если  при
при  .
Соответственно, алгоритм решения задачи (*) выглядит так:
.
Соответственно, алгоритм решения задачи (*) выглядит так:
а) выбираются точка  , в
которой
, в
которой  и монотонно убывающая сходящаяся к нулю
последовательность положительных чисел
и монотонно убывающая сходящаяся к нулю
последовательность положительных чисел 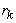 ;
;
б) при k = l, 2, ...,
начиная с точки  , полученной на предыдущей
итерации, решается задача безусловной минимизации по х функции
, полученной на предыдущей
итерации, решается задача безусловной минимизации по х функции
 ,
,
в
результате чего определяется очередная точка  .
.
Пусть  - решение задачи
безусловной минимизации
- решение задачи
безусловной минимизации , где функция
, где функция  определена равенствами (**) или (***).
Полагая
определена равенствами (**) или (***).
Полагая 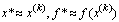 для достаточно большого k, находим
приближенное решение задачи нелинейного программирования (*) методом барьерных
функций. Для контроля достигнутой точности решения можно использовать следующий
критерий
для достаточно большого k, находим
приближенное решение задачи нелинейного программирования (*) методом барьерных
функций. Для контроля достигнутой точности решения можно использовать следующий
критерий
 .
.
Методы внешних штрафных функций
В методах внешних штрафных функций штрафы  , сходящиеся при k®¥ к индикаторной функции, строят так, чтобы при всех k
было
, сходящиеся при k®¥ к индикаторной функции, строят так, чтобы при всех k
было
 = 0 для хÎW
= 0 для хÎW
и
 >0 для xÏW.
>0 для xÏW.
Обычно, как и в методах барьерных функций, полагают
 ,
,
только
теперь 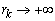 при
при  и F(х) есть функция, определенная на всем пространстве значений x,
равная нулю на множестве W и положительная за его
пределами. Для задач с ограничениями вида
и F(х) есть функция, определенная на всем пространстве значений x,
равная нулю на множестве W и положительная за его
пределами. Для задач с ограничениями вида
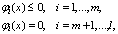
наиболее
распространены две функции F(х):
 ,(∆) или
,(∆) или  ,(∆∆)
,(∆∆)
где  -
«срезка» функции
-
«срезка» функции  :
:

Достоинство функции (∆) по сравнению с
(∆∆) в том, что если  , непрерывно
дифференцируемы, она также будет обладать этим свойством (рис. 8.2).
Соответственно, при реализации использующего ее алгоритма для поиска минимумов
по х функций
, непрерывно
дифференцируемы, она также будет обладать этим свойством (рис. 8.2).
Соответственно, при реализации использующего ее алгоритма для поиска минимумов
по х функций

можно
применять градиентные методы. В то же время гладкая функция (∆∆)
хороша тем, что уже при конечном значении  обеспечивает
совпадение точки безусловного минимума суммы
обеспечивает
совпадение точки безусловного минимума суммы  с
решением исходной задачи
с
решением исходной задачи 

|
Рис. 8.2.
|
Рис. 8.3
|
Правда, достаточно
эффективных алгоритмов минимизации негладких штрафных функции пока нет, и
поэтому чаще все же используют гладкий квадратичный штраф. По этой причине и мы
в дальнейшем ограничимся рассмотрением алгоритма с гладкой внешней штрафной
функцией. Он состоит в следующем:
а) выбираются произвольное начальное приближение  и монотонно возрастающая
последовательность чисел
и монотонно возрастающая
последовательность чисел  ;
;
б) при k =1, 2, .... начиная с  , решается задача безусловной
минимизации по х функции
, решается задача безусловной
минимизации по х функции
 ,
,
в
результате чего определяется очередное приближение  к
решению исходной задачи.
к
решению исходной задачи.
При определенных условиях последовательность решений
задач безусловной минимизации сходится к решению х* исходной
задачи с ограничениями
 ,поэтому для
достаточно больших k полагают
,поэтому для
достаточно больших k полагают  .
Критерием достижения требуемой точности может служить неравенство
.
Критерием достижения требуемой точности может служить неравенство 
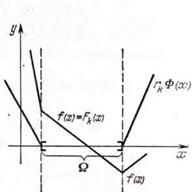

![]() при ограничениях
при ограничениях
![]()
 (1.1)
(1.1)![]() некоторую
полуплоскость. Полуплоскость – выпуклое множество. Но пересечение любого числа
выпуклых множеств является выпуклым множеством. Отсюда следует, что область
допустимых решений задачи (1.1) есть выпуклое множество.
некоторую
полуплоскость. Полуплоскость – выпуклое множество. Но пересечение любого числа
выпуклых множеств является выпуклым множеством. Отсюда следует, что область
допустимых решений задачи (1.1) есть выпуклое множество.
![]() получаем
ур-ие прямой. Изменяя знач-е, характеризующее линию ур-ня F0 , получим семейство параллельных прямых.
получаем
ур-ие прямой. Изменяя знач-е, характеризующее линию ур-ня F0 , получим семейство параллельных прямых.![]() . Если цел-ая ф-ия лин-на, то ее
частн. произв-ые равны коэф-ам при перем-ых и постоянны в любой (×).
. Если цел-ая ф-ия лин-на, то ее
частн. произв-ые равны коэф-ам при перем-ых и постоянны в любой (×). ![]()

![]() ;
;![]() )
наискорейшего возрастания целевой функции – вектор градиентного направления.
)
наискорейшего возрастания целевой функции – вектор градиентного направления.