Системы счисления

 

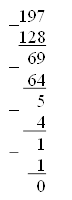
Представление данных в ЭВМ в силу физических законов ее функционирования не может осуществляться на основе десятичной системы счисления. Базовым элементом любой цифровой ЭВМ является так называемый ключ, поведение которого характеризуется двумя состояниями – включено (1), выключено (0), то есть состояние этого ключа (так же множество других ключей) в ЭВМ может быть описано с помощью двух цифр: нуля и единицы. Эти соображения послужили причиной применения двоичной системы счисления. Все цифры в числе определяются ее порядком.

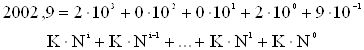
K – принимает значение любой цифры данной системы счисления; N – основание данной системы счисления; i – номер позиции (показатель степени), которая цифра занимает в числе.

 

 

 

Примеры.

a)              

b)              

c)                11000101

 

 

 

 

 

 

 

Существенным недостатком двоичной системы счисления является то, что для представления больших чисел необходимо большое количество двоичных разрядов, а это, в свою очередь, приводит к уменьшению надежности в представлении двоичных чисел. Имеется в виду, что вероятность возникновения ошибки с увеличением разрядности числа возрастает, кроме того, двоичная система счисления не является компактной. С другой стороны, отказываться от этой системы мы не можем, поэтому в качестве обоснованного компромисса используется шестнадцатеричная система счисления. Ее достоинством является компактность в записи больших чисел и просмотра при переходе от  шестнадцатеричной к двоичной и обратно системах счисления.

Например.

a)               0110.0011.1100.1011.0011 = 63CB3

b)               1111.0000.1010.0111 = FØA7

 

Сигналы

 

Обмен информацией в системах происходит при помощи сигналов. Носителями сигналов являются физические величины. Например: ток, напряжение, электромагнитные колебания, световые или акустические волны и т. п. Эти физические величины представляют собой функции времени. Определяющие параметры, передаваемых временных функции, такие как частота, амплитуда, фаза, длительность и другие называются информационными параметрами в том случае, когда посредством этих параметров передается эта информация. Если физическая величина является носителем двух и более информационных параметров, то его называют многомерным. Различают следующие виды сигналов:

·                   Аналоговые – это сигналы, информационные параметры которого внутри заданного диапазона могут принимать любые значения.

·                   Дискретные – это сигналы, информационные параметры которого внутри заданного диапазона могут принимать лишь определенные дискретные значения.

·                   Непрерывные - это сигналы, информационные параметры которого могут изменяться в любой момент времени.

·                   Прерывистые - это сигналы, информационные параметры которого могут принимать другие значения лишь в дискретные моменты времени.

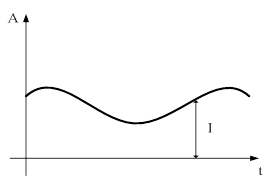
Аналоговый сигнал (непрерывный). Информационный параметр – амплитуда.

 

 

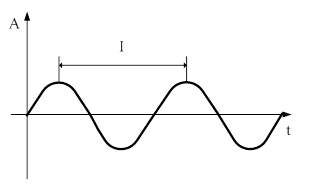
Частотно-аналоговый сигнал (непрерывный). Информационный параметр – частота.

 

Сигнал опроса (аналоговый, прерывистый). Информационный параметр – амплитуда.

 

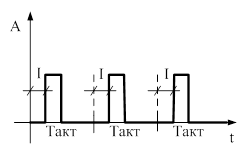
Импульсный сигнал (аналоговый, прерывистый). Информационный параметр – фаза (положение импульса  в пределах такта).

 

 

 

 

 

 

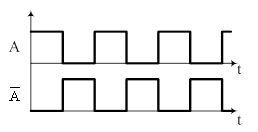
Двоичный (двухпозиционный) сигнал (дискретный, непрерывный). Информационный параметр – два значения нуля или единицы.

 

Время, за которое сигнал изменяется от низкого уровня (0) до высокого уровня (1) называется временным нарастания переднего фронта (t_п.ф.). И обратно, время перепада из высокого уровня на низкий называется временем спада заднего фронта (t_з.ф.).

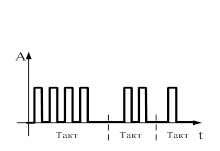
Импульсно – счетный сигнал (дискретный, прерывистый). Информационный параметр - число двоичных импульсов в пределах такта.

 

Логические состояния

 

Под цифровой электроникой понимают такие схемы, для каждой точки которой можно определить, как правило, только два состояния. Обычно в качестве параметра выбирают напряжение, уровень которого может быть «высоким» или «низким». Эти два состояния могут представлять различные биты информации. Например, ключ замкнут или разомкнут, событие произошло, либо нет, сигнал присутствует, либо отсутствует. Состояние уровней («высокие» и «низкие»), некоторым заданным образом, определяют «истинное», либо «ложное» значение переменных в алгебре логики (Булева алгебра).

Введем понятие 1 и Ø. Эти символы используются в алгебре логике для обозначения утверждения, «истина» и «ложь» соответственно. В электронике 1 и Ø обозначают соответственно «высокий» и «низкий» уровень напряжения. Для различных типов цифровых схем уровень 0 и 1 всегда известны, поэтому нет необходимости обозначать эти уровни абсолютными значениями напряжений. То есть, по сути, этот вопрос является соглашением по умолчанию.

Например, персональный ЭВМ типа IBM PC, уровень логической 1 соответствует уровню напряжения от 2,4 до 5 В («1» → 2,4 ÷ 5 В), а уровень «Ø» → 0 ÷ 0,4 В.

 

Логические элементы и таблица истинности

 

В основе всех цифровых систем лежат четыре основных логических  элемента (операций):

1.                Логическое сложение, дизъюнкция, ИЛИ

2.                Логическое умножение, конъюнкция, И

3.                ИЛИ - исключающее

4.                Отрицание, НЕ

Все эти элементы обладают свойством функциональной полноты, т.е. на их основе может быть решена любая логическая непротиворечивая функция.

В электротехнических системах логические элементы принято обозначать в виде прямоугольников со сторонами кратным 5 мм, причем, слева показаны входы, справа выходы.

 

 

 

 

 

Входные величины по правилам алгебры логики обозначаются, как правило, заглавными латинскими буквами (A, B, C…), так же обозначаются и выходные переменные. Связь между входами и выходами определяется конкретной логической функцией.

 

 

         

 

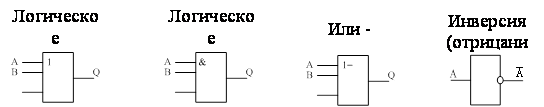Одним из основных инструментов для анализа цифровых комбинационных схем на этих элементах является таблица истинности, которая состоит из N – столбцов, где N – 1 равно количеству входных переменных. А последний столбец принимает значение выходной переменной. Если количество входных переменных равно K, то количество строк в этой таблице равно 2^K. Важной особенностью всех входных и выходных переменных в алгебре логике является то, что все они могут принимать только два значения – нуля или единицы.

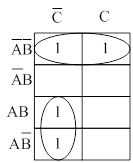
Логическое сложение, дизъюнкция, элемент ИЛИ

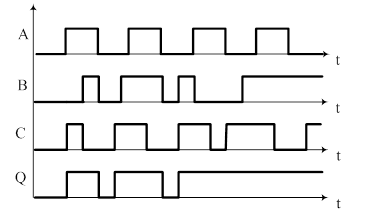
Для обозначения операции ИЛИ в алгебре логике используется символ «+». Например, A или B = A + B.

Примем, что если ключ A (B) замкнут, то А (В) равно единице, и наоборот, если разомкнут, то A (B) равно Ø. Если лампочка Q горит, то Q=1, если не горит, то  Q=Ø.

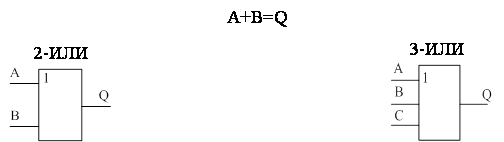Анализ выполним с помощью таблицы истинности. Выходными переменными являются А и В, выходной переменной – Q.

 

 

 

 

 

 

 

 

A	B	C	Q
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

A	B	Q
0	0	0
1	0	1
0	1	1
1	1	1

 

 

 

 

 

 

 

 

 

 

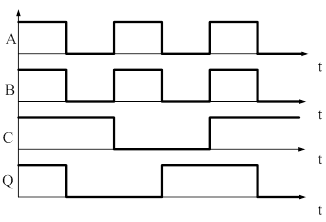
Все физические процессы протекают и исследуются, как правило, во времени, поэтому чтобы знать, когда и как произошло, то или иное событие используются диаграммы состояний.

 

 

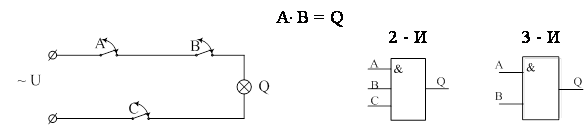
Логическое умножение, конъюнкция, элемент И

В алгебре логике операция логического умножения обозначается символом умножить «·». Например, А и В = .

 

 

 

 

 

A	B	Q
0	0	0
0	1	0
1	0	0
1	1	1

A	B	C	Q
0	0	0	0
1	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	1	0
1	1	0	0
1	1	1	1

 

 

 

 

 

 

 

 

 

 

 

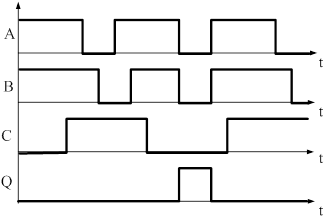
Диаграмма состояний для этой функции изображается так же:

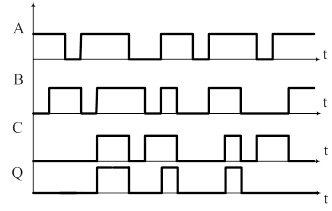
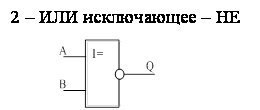
ИЛИ – исключающее

Для обозначения этой операции в алгебре логике используют символ . Например, АВ=Q.

Проиллюстрировать работу этого элемента с помощью ключей и лампочки невозможно, поэтому необходимо знать таблицу истинности.

 

 

 

 

 

 

 

A	B	Q
0	0	0
0	1	1
1	0	1
1	1	0

A	B	C	Q
0	0	0	0
0	1	1	1
1	0	1	1
1	1	0	1
1	1	1	0

 

 

 

              

 

 

 

 

 

логический элемент не, отрицание, инверсия

Часто бывает необходимо получить дополнения (инверсию) логического сигнала. Эту операцию выполняет инвертор. Эта схема имеет один вход и выход.

 

 

 

 

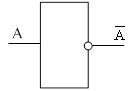В алгебре логическое отрицание обозначается чертой над переменной. На электрических схемах отрицание обозначается кружком у соответствующего выхода или входа.

В соответствии с американским электротехническим стандартом (ASCII) логические элементы изображают:

 

 

 

 

Комбинированные логические элементы

 

Для удобства и упрощения проектирования, а также  изготовления цифровых систем используются множество элементов, которые в себе объединяют несколько базовых функций.

 

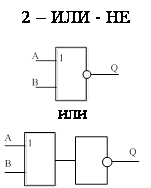логическое сложение с отрицанием

(N –Или – не, где N – количество входов элемента)

 

 

 

 

 

 

Этот элемент обладает свойством функциональной полноты, то есть на его основе может быть реализована любая логическая непротиворечивая функция.

 

 

A	B	Q
0	0	1
1	0	0
0	1	0
1	1	0

 

 

 

 

 

 

 

 

 

 

 

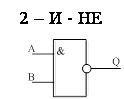
Элемент логического умножения с отрицанием

(N – И – Не, где N – количество входов элемента)

В соответствии с правилом де Моргана этот элемент так же обладает свойством функциональной полноты.

A	B	Q
0	0	1
1	0	1
0	1	1
1	1	0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

элемент или - исключающее с отрицанием

(N – ИЛИ – исключающее – НЕ, где N – количество входов элемента)

Так же обладает свойством функциональной полноты.

 

A	B	Q
0	0	1
1	0	0
0	1	0
1	1	1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

построение схем по логическому выражению

 

Схема электрическая - принципиальная является графической, топологической моделью, отображающая поведение реального физического объекта.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПОСТРОЕНИЕ СХЕМ НА ОСНОВЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ В ДИЗЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМЕ (ДНФ)

 

 

 

 

 

 

 

 

 

 

На основе анализа данной конкретной задачи из ее содержания выделяются все исходные двоичные переменные (входные и выходные). Этим переменным присваиваются имена в соответствии с правилами алгебры логики.

После этого строится таблица истинности в следующей последовательности:

·                   Определяется количество строк в таблице из условия 2ⁿ, где n – количество строк входных двоичных переменных.

·                   Присваиваем имя выходной переменной (например, Q).

·                   Количество столбцов в таблице будет равно N + 1.

·                   Заполняются все столбцы таблицы, кроме крайнего правого. Это делается таким образом, чтобы перебрать все возможные комбинации 0 и 1 из 2ⁿ.

·                   В соответствии с условием исходной задачи заполняется столбец выходной переменной, причем 1 вписывается в те строки, где комбинации входных переменных дают истину по условию задачи, а в остальные строки вписываем 0.

·                    Выделяют те строки, результат в которых равен 1 и пересечением их в алгебраической форме, причем, если в данной строке входная переменная равна 1, то это означает равенство самой себе в алгебраическом выражении. Если же переменная равна 0, то в выражении она записывается с отрицанием.

·                   Конечное алгебраическое выражение представляет собой логическую сумму частных произведений, образованных соответствующим перемножением переменных в строках для которых перемноженная строка равна 1.

 

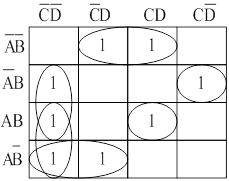
минимизация логических выражений с помощью карт карно

Часто полученное из таблицы истинности выражение в ДНФ является громоздким, избыточным и поэтому может быть упрощено – минимизировано. Такие упрощения дают значительную экономию материальных ресурсов при проектировании и изготовлении цифровых систем. Другим важным следствием упрощения является повышение надежности системы в целом.

 

 

 

 

 

карта карно для двух переменных

Четыре квадрата соответствуют четырем возможным комбинациям А и В в таблице истинности с двумя переменными. При этом квадрат 1 соответствует произведению , квадрат 2 соответствует произведению , квадрат 3 - , квадрат 4 - .

Например.

 

 

 

 

 

 

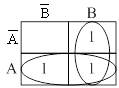
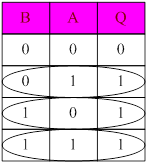
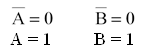
Из этой таблицы истинности видно, что по известным правилам получаем логическое выражение в ДНФ.

В записи карт Карно соседние единицы объединяются в контуры группами по 2, 4, 8, и т. д. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Каждый контур представляет собой новый член упрощенного логического выражения. Возьмем сначала нижний контур, заметим, что переменная А здесь встречалась в комбинации с В и . В соответствии с правилами алгебры логики В и  дополняют друг друга и тогда в нижнем контуре остается только первый член А. В другом контуре вместе с В встречается так же А и , что  также является дополнением и поэтому во втором контуре остается один член В. Полученное таким образом в каждом контуре выражение объединяются логической функцией «сложение». В результате получим упрощенное выражение  А + В.

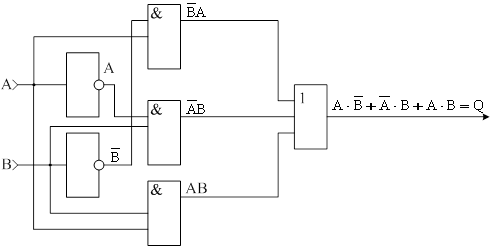
Последовательность операций, при упрощении логических выражений с помощью карт Карно:

·                   Получение логического выражения в ДНФ, как правило, из таблицы истинности.

·                   По этому логическому выражению заносятся единицы в соответствующие клетки карты Карно.

·                   Эти единицы в карте Карно объединить в контуры, охватывающие 2, 4, 6 и т. д. соседних единиц.

·                   Проводим упрощение путем исключения членов в контуре дополняющих друг друга.

·                   Полученное таким образом в каждом контуре выражения объединяются логической функцией «ИЛИ».

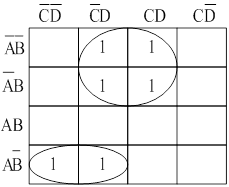
карта карно с тремя переменными

Оно имеет следующий вид:

 

 

 

 

Нижний контур содержит дополнения В и , остается ,  верхний контур содержит С и , поэтому остается . Эти новые члены объединяются логическим сложением.

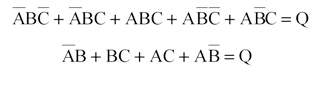
карта карно для четырех переменных

Правила заполнения и группировки остаются прежними.

Например.

1.)  

 

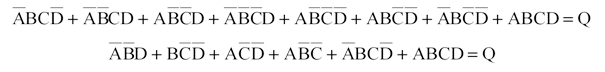2.)

     

 

К их недостатку можно отнести то, что построение карт Карно больших размерностей невозможно в простом виде на плоскости.

 

комбинационные функциональные схемы

При проектировании цифровых схем разработчик часто сталкивается с некими типовыми схемными реализациями, то есть ряд функций встречаются часто и поэтому они были реализованы  в виде интегральных микросхем среднего уровня интеграции.

счетверенная двухвходовая схема выборки

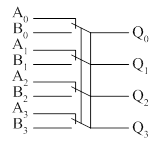Если контакт нормально замкнут, то Q_i=A_i, при переключении ключей в нижнее положение Q_i=B_i. Это и есть схема, счетверенная двухвходовая схема выборки. Приведенная схема обладает рядом  существенных недостатков: 

1.                низкая скорость переключения (от 0,3 до 0, 05 сек.).

2.                неопределенность состояния выхода и входа в момент времени, когда подвижный контакт уже отошел от нормально - замкнутого, но еще не дошел к нормально – разомкнутому.

3.                при замыкании контактов в силу их упругости возникает так называемый «дребезг».

4.                низкая надежность электромеханических переключателей (даже  у лучших переключателей порядка 10 – 15 тысяч переключений).

5.                высокая стоимость электромеханических переключателей.

Для преодоления всех этих недостатков были разработаны электронные бесконтактные переключающие устройства. Скорость переключения – 10^-9 сек. Полная определенность при переключении, - количество переключений практически не ограничено, надежность – выше, цена – ниже.

На схемах электрически принципиально счетверенную двухвходовую схему изображают:

Схемы имеют 10 входов и 4

выхода. Входа A_i и B_i называются информационными, то есть на них от внешнего источника подаются входные логические

E	SEL	Аi	Bi	Qi
В	X	X	X	H
Н	H	H	X	H
Н	H	B	X	B
Н	B	X	H	H
Н	B	X	B	B

сигналы, уровнем  или 0, или 1. Вход SEL – выбор, если на него подать низкий уровень (Н), то  Q_i=A_i. Если SEL = 1, то Q_i=B_i.

Е – управляющий вход – разрешение. Х – безразличное состояние.

Если Е=1, то схема отключена и независимо от того, чему равно А, В, и SEL, то Q=0 (H). Если Е=0, то схема включается, а состояние выхода Q определяется значением сигнала на входе SEL и информационных входах.                                                                           

 

 

 

 

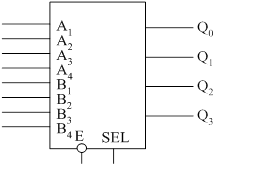
мультиплексоры

Бывают двух, четырех, восьми и шестнадцати                                     входовые схемы.

Состояние выхода Q однозначно определяется положением подвижного контакта, при переключении. На рисунке Q = A₁.

 

На схемах электрически принципиально мультиплексор изображают:

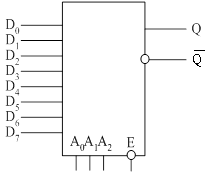
Схема имеет 8  информационных входов D₀ – D₇ (на них подаются логические сигналы), 3 адресных входа A₀ – A₂, управляющий вход Е – разрешение. Прямой выход Q и инверсный выход .

 Когда схема выключена, то есть Е=1, то независимо от того, чему равны все остальные входа схемы Q=0 (). Когда Е=0 схема включается и состояние выхода Q=D_i в зависимости от значения адреса на входах А₀, А₁, А₂.  

При проектировании логических устройств может возникнуть необходимость в мультиплексировании большего числа входов, чем есть у выбранной схемы. Эта проблема возникает часто и не только при мультиплексировании. Она  решается с помощью расширения или наращивания на основе более простых схем. При этом разработчик этих схем заранее предусмотрел возможность наращивания.

 

 

 

 

E	А2	А1	А0	Q
1	X	X	X	0
0	0	0	0	D0
0	0	0	1	D1
0	0	1	0	D2
0	0	1	1	D3
0	1	0	0	D4
0	1	0	1	D5
0	1	1	0	D6
0	1	1	1	D7

 

 

 

 

 

 

 

 

 

 

 

 

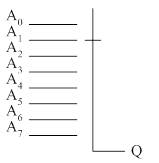
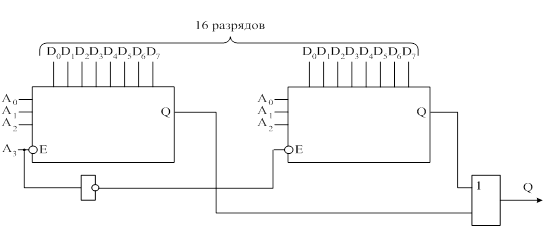
Рассмотрим, например, схему шестнадцатиразрядного мультиплексора, построенного на двух интегральных схемах восьмиразрядного мультиплексора.

 

 

 

 

 

 

 

А3	А2	А1	А0
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
. . .	. . .	. . .	. . .
1	1	1	1

До тех пор, пока значение адреса не превышает 7 – старший разряд А₃=0. Он подается на вход Е первой схемы и через инвертор на вход Е второй схемы, то есть первая схема включена, а вторая - отключена. Таким

образом, на первый вход схемы ИЛИ от второго мультиплексора поступает 0 независимо от состояния остальных входов этой схемы. А выход i – ой схемы равен значению, на который указывает 3 младших разряда адреса.

 

 

сумматоры

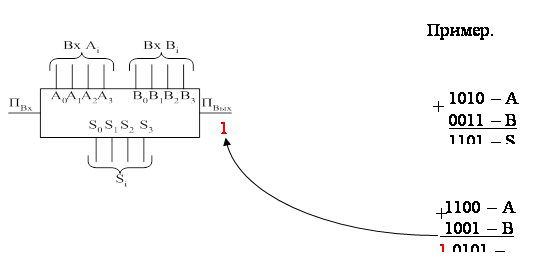
Сумматоры – схема складывает четырехразрядное двоичное число А_i c четырехразрядным двоичным числом В_i и на выходе формирует двоичную сумму S_i. Для расширения сумматора в схеме предусмотрен вход переполнения П_вх и выход переполнения П_вых. На схемах электрически – принципиальных изображают следующим образом:

 

 

        

 

 

 

 

 

      

Рассмотрим пример сложения двух восьмиразрядных чисел.

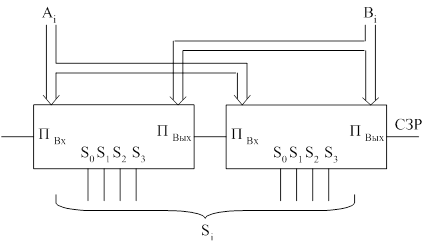
СЭР – старший значащий разряд.

Если сумма S_i ≥ 256 (2⁸), то СЗР = 1. В противном случае – ноль. Вход левого сумматора принудительно обнулен, так как с этой стороны нет расширения.

Сумматоры являются одним из важных устройств, входящих в состав микропроцессора. На его основе построено арифметическое логическое устройство (АЛУ) процессора.

компараторы

Компаратор (от латинского сравнивать) – определяет относительные значения двоичных чисел А и В и вырабатывает на входе сигналы, соответствующие соотношениям:  A > B, A = B, A < B. Входы и выходы компаратора предусматривают возможность расширения.

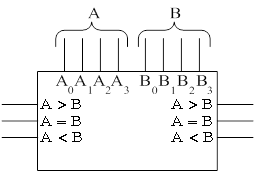
Команды сравнения относятся к группе арифметических и обязательно входят в состав команд любого микропроцессора.

 

 

двоичная арифметика

Так как информационные процессы в цифровых системах принимают значения только 0 и 1, то и представления данных осуществляется с помощью двоичных чисел. Сложение и вычитание двоичных чисел, а так же и все остальные арифметические действия выполняются по тем же правилам, что и в десятичной арифметике.

 

сложение двоичных чисел

 

 

 

 

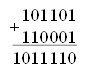вычитание двоичных чисел

 

 

 

 

умножение двоичных чисел

 

 

 

 

 

 

 

 

 

 

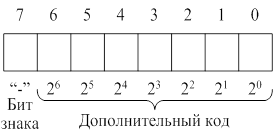
дополнительный код

Если нужно использовать числа со знаком, в ЭВМ используется специальный код. Применение его существенно упрощает аппаратные средства ЭВМ.

Изобразим условно ячейку памяти или регистр ЭВМ.

1 – имеет вес 16 (2⁴).

Для представления знака числа принято соглашение о том, что если старший значащий разряд в числе равен нулю, то число положительное.

В остальных ячейках записывается второе параллельное число. Если старший разряд слова равен 1, то число является отрицательным, а в остальных рядах слова записано двоичное число в дополнительном коде.

Использование дополнительного кода позволяет операцию вычитания заменить сложением.

Выполним преобразование отрицательного числа (-9) в дополнительном коде:

·                   Преобразуем число 9 в двоичный эквивалент – 00001001. Слева допишем нули, если это необходимо до 8 – разрядного числа.

·                   Выполним разрядную операцию отрицания с этим числом (проинвертировать число). Операция сведется к замене 0 – 1, а 1 – 0.

Получим:

                 

 

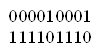
·                   К полученному числу прибавить 1.

 

 

 

Полученное число является дополнительным кодом отрицательного числа (-9). На это указывает 1 в старшем разряде.

обратные преобразования, записанные в дополнительном коде

Число отрицательное, т.к. на это указывает 1 в старшем разряде.

Выполняем инверсию этого числа: 00110010.

К полученному числу прибавляем 1.

 

 

 

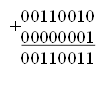
Это число является модулем исходного числа, записанного в дополнительном коде.

арифметика в дополнительном коде

Процессоры ЭВМ неприспособленны для выполнения операций вычитания, поэтому эту операцию заменили операцией сложения, в которой отрицательные числа представлены в дополнительном коде.

Рассмотрим на примерах все возможные ситуации, при арифметических действиях с числами:

1.                сложение двух положительных чисел:

 

 

 

 

 

2.                сложить числа:

 

 

 

 

 

 

 

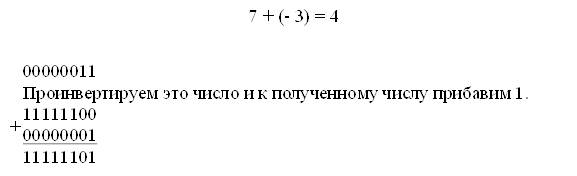В результате получили девятиразрядное число, причем старший разряд является переполнением восьмиразрядного числа, поэтому им пренебрегаем.

Оставшееся число в старшем разряде имеет 0, поэтому является положительным.

3.                Сложить 2 отрицательных числа:

 

 

 

 

 

 

 

 

 

 

 

Выполним обратное преобразование:

 

 

 

 

последовательная логика

 

Все схемы, рассматриваемые ранее, строились на основе комбинационной логике. Для таких схем состояние выхода полностью определяется текущим состоянием выходов, то есть у таких схем отсутствует предыстория (предыдущее состояние не влияет на текущее). 

          Наличие памяти позволяет строить системы с очень большими возможностями. Под элементом памяти мы будем понимать устройство, которое под действием управляющих сигналов может сохранять свое состояние на выходе неопределенно долгое время, а так же текущее состояние этого элемента неким заданным образом связано с предысторией.

 

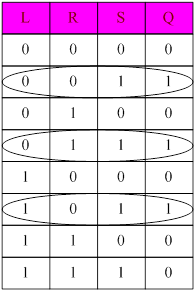
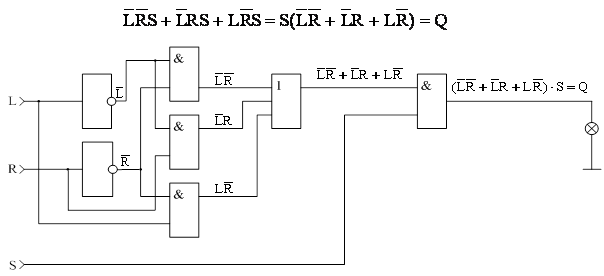
RS – триггер

Многие виды памяти в цифровых системах реализуются на основе триггеров.

Триггер – цифровое устройство с двумя устойчивыми состояниями выхода, причем состояние выхода определяется текущим состоянием входов и предыдущим состоянием триггера. RS – триггер имеет два входа S (Set) и R (Reset), а так же имеет два выхода Q – прямой и - инверсный.

R	S	Q
0	1	1	0
1	1	1	0
1	0	0	1
1	1	0	1
0	0	1	0

 

 

 

 

 

 

 

 

 

 

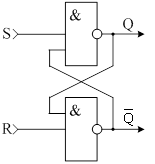
На схемах электрических принципиальных RS – триггер изображают:

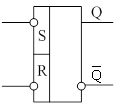
Если мы говорим, что в триггер записана 1, то это означает, что под действием управляющих входов Q = 1.

Для анализа работы этой схемы удобно пользоваться диаграммой состояния.

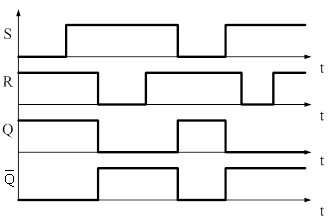
Важной особенностью работы триггеров является то, что, как правило, мы не знаем состояние триггера в момент включения, поэтому либо принимаем какие-то специальные меры или если это не важно, то произвольно задаются любым состоянием.

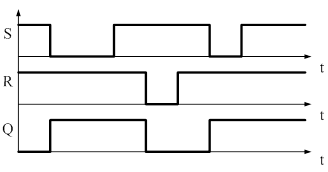
Рассмотрим примеры применения RS – триггера:

1.                Фиксация кратковременных событий.

 В различных научных и технологических задачах встречаются ситуации, когда некое важное событие существует очень короткое время, а знание о том, произошло это событие или нет, является очень важным. Используя свойства RS – триггера сохранять свое предыдущее состояние позволяет решить эту задачу.

 

 

 

 

 

 

 

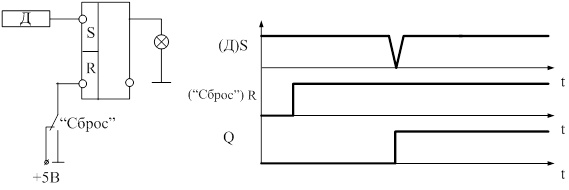В начальный момент времени кратковременно нажимаем кнопку «Сброс», т. е. на R – вход подаем 0. В это время на выходе датчика Д = 1 (событие не произошло), т. е. S=1, R=0. В соответствии с правилами RS – триггера Q=0. Это состояние будет сохраняться до тех пор, пока на выходе датчика не появится сигнал 0. В этот момент времени S=0, а R=1. Триггер “опрокинется” (изменит свое состояние на противоположное) Q=1. После того, как сигнал кончился (S=1, R=1) и триггер сохраняет свое предыдущее состояние до того момента, пока мы не нажмем кнопку «Сброс».

2.  Бездребезговая кнопка.

Механические контакты переключателей изготавливаются, как правило, из упругих токопроводящих материалов, а это означает, что в силу своей упругости контакт при переключении может несколько раз отскочить и вернуться в исходное положение. Если такая кнопка находится в системе управления, то эта система воспримет ситуацию дребезга как несколько нажатий на кнопку, а это приведет к неадекватной реакции.   

На диаграмме это выглядит так:

 

 

 

 

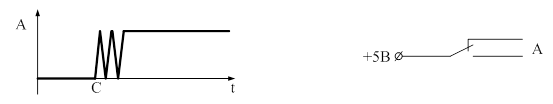
Используя наши знания RS – триггера можно построить схему, исключающую дребезг механических контактов.

 

 

 

 

 

 

 

 

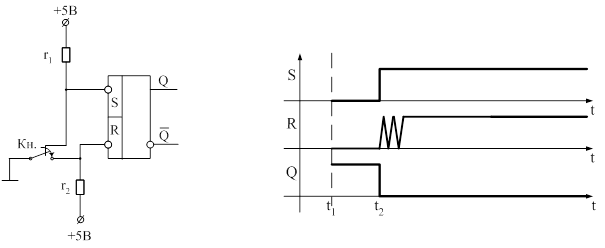
Схема включает в себя следующие элементы: RS – триггер, резисторы r₁ и r₂, кнопка (Кн.), дребезг которой необходимо подавить. Резисторы r₁ и  r₂ одним своим выводом подключены к источникам ЭДС +5В (1), а другим к выходам R и S соответственно. Подвижный контакт кнопки подключен к Земле (0). В исходном состоянии подвижный контакт кнопки через нормально замкнутый контакт подключен к S – входу, т. е. S=0, а нормально разомкнутый контакт имеет  потенциальный контакт +5В через регистр r₂ и подключен к R – входу (1). Таким образом, по правилу работы  RS – триггера в момент времени t₁, Q=1. В момент времени t₂ произошло переключение кнопки и на нижнем ее контакте образовался «дребезг». Однако, в момент t₂ на S – вход через регистр r₁ подается уровень логической единицы.

В момент первого касания (t₂) подвижного контакта нижнего контакта на R – вход от подвижного контакта подается 0. И по правилам работы RS – триггера (S=1, R=0) триггер опрокинется, т.е. Q=0. Дальнейшее срабатывание кнопки, вызванное дребезгом, не изменит состояние триггера, т.е. на выходе Q  дребезг не наблюдается.

 

 

 

 

регистры

 

Это устройство, предназначенное для временного хранения и / или преобразования двоичной информации.

Различают несколько типов регистров:

·                   Параллельно – параллельное – запись и считывание информации в двоичном параллельном коде.

·                   Параллельно – последовательное – запись информации в параллельном формате, а считывание в последовательном.

·                   Последовательно – параллельное – запись в последовательном формате, а считывание в параллельном.

·                   Последовательно – последовательное – запись проводится в последовательном формате, а считывание в последовательном.

·                   Универсальные регистры – регистры, которые при помощи управляющих сигналов могут перенастраиваться на любой тип считывания и записи информации.

 

параллельно – параллельный четырехразрядный регистр на RS – триггерах

 

 

 

 

 

 

 

 

 

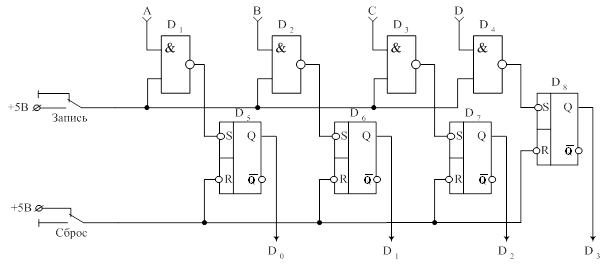
Схема предназначена для хранения двоичной информации в параллельном входе на выходах D₀ … D₃  и поступления на входа A, B, C и D. Запись и перезапись информации в регистре осуществляется с помощью управляемых сигналов «Запись» и «Сброс».  

В момент включения схемы состояние выходов триггеров не определено. Кнопка «Запись» в нормальном состоянии подает на 2 входа D₁, D₂, D₃, D₄ уровень 0. Независимо оттого, что на 2 входах этих элементов на выходе 1. Кратковременно нажимается кнопка «Сброс», т.е. на R – входах кратковременно 0, S=1. Поэтому D₀ … D₃  равно 0. Когда нам необходимо в регистр записать входную информацию, кратковременно нажимается кнопка «Запись», при этом на 2 входах элемента  D₁, D₂, D₃, D₄ подается уровень логической единицы, а это означает, что если, например, А=1, то на выходе 0. Этот ноль подается на S-вход D₅, R=1 – в триггер запишется 1, т.е. А= D₀. Если, например, А=0, «Запись» равна 1, на выходе элемента D₁ – 1. Следовательно, триггер D₅ сохранит предыдущее состояние (0), т.е. А= D₀ .

 

D – триггер

 

Существенным недостатком RS – триггера является то, что момент изменения его состояния фактически нам не известен, т.е. его переключение зависит не от нас, а от некого текущего состояния на его входах. Этот недостаток преодолевается с помощью динамических триггеров. Используют 2 типа таких триггеров: D – триггер и JK – триггер.

D – триггер представляет собой устройство имеющее 4 входа и 2 выхода. Его изображают следующим образом:

Входа S и R (установка, сброс) являются входами стандартного RS – триггера, входящего (встроенного) в D – триггер. Эти входа имеют высший приоритет по сравнению с остальными входами триггера. Это означает, что если хотя бы на одном из этих двух входов присутствует уровень логического нуля, то в независимости от того, что  в этот момент на других входах D и C, весь триггер работает по правилам обычного RS – триггера. Когда S=R=1 включается собственно D – триггер. D – информационный вход, C – тактирующий. Направление стрелки у С – входа указывает на то, что триггер тактируется (чувствует) передним фронтом тактового импульса. Передний фронт – изменение из низкого уровня в высокий, а задний фронт, наоборот, из высокого в низкий.

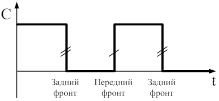
Правило работы D – триггера состоит в следующем (S=R=1),что информация (0 или1) присутствует на информационном входе D, записывается в триггер (на Q - выход) в момент появления переднего фронта импульса на тактирующий вход C. 

Примеры.

1.)

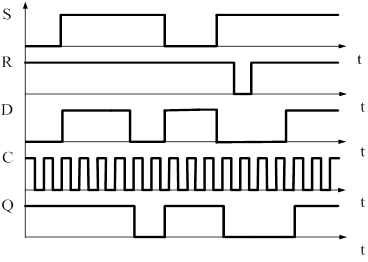
2.)

 

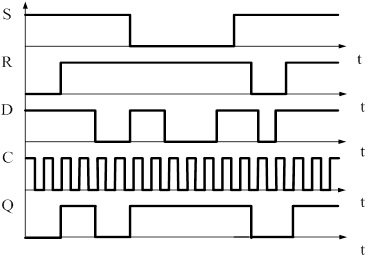
счетный триггер

Образуется из D – триггера, при непосредственном соединении - выхода с D – входом.

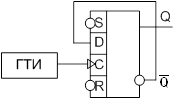
На схеме входа S и R некуда не подключены (висят в воздухе). По принятым соглашениям все входа логических элементов, которые никуда не подключены, имеют значения равные 1(S=R=1).

ГТИ – генератор тактовых импульсов – устройство, на выходе которого формируется напряжение прямоугольной формы, амплитуда этого напряжения соответствует уровню логической единицы,  а период следования импульсов задается нужным.

Так как в момент включения схемы мы не можем сказать чему равно Q, то для простоты примем Q=0.

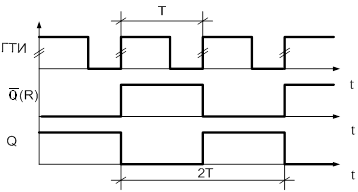
В начальный момент времени Q=0, следовательно, =1=D. Передний фронт тактового импульса от ГТИ (t=0) перепишет 1 с D – входа на Q – выход, следовательно,  станет равным 0 и равным D. Состояние триггера, до прихода следующего переднего фронта тактового импульса, не изменится. Следующий передний фронт изменит состояние триггера на противоположное. И т.д. – процедура циклически повторяется. Заметим, что период следования импульсов на прямом выходе триггера в два раза больше периода следования импульсов от ГТИ.

 

счетчики

Это устройство, которое широко применяется в различных цифровых системах, в том числе и в ЭВМ.

Счетчик – устройство, состояние выхода которого зависит от количества событий на его выходе. Часто состояние выхода равно количеству событий на входе. Различают следующие виды счетчиков:

·                   На сложение – когда состояние счетчика увеличивается на +1 с каждым новым событием.

·                   На вычитание -  когда состояние счетчика уменьшается на -1 с каждым новым событием.

·                   Реверсивный счетчик – счетчик, направление счета которого можно изменить, при помощи управляемых сигналов.

 

 

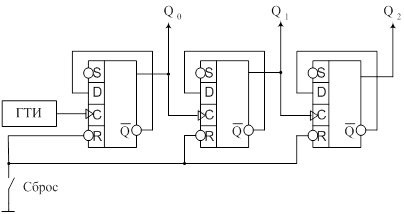
счетчик на сложение

 

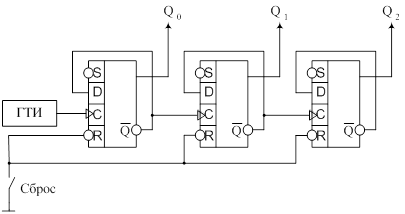
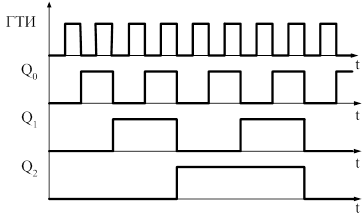
На схеме представлен трехразрядный двоичный счетчик, собранный на трех счетных триггерах таким образом, что каждый следующий триггер тактируется от инверсного выхода предыдущего. Источником событий будем считать тактовые импульсы от ГТИ, а выходом - двоичный параллельный код с прямых выходов триггеров. Причем, младший значащий разряд слева - Q₀, а старший справа - Q₂.

         До начала эксперимента (t=0), кнопка «Сброс» нажата, т.е. на все R – входа подается низкий уровень напряжения Земли. На всех S – входах в это время 1 и по правилам работы RS – триггера (Q₀=Q₁=Q₂=0) следует, что не все - выхода равны 1, следовательно, D – входа равны 1.

 

 

 

N	Q2	Q1	Q0
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1
8	0	0	0

В момент времени t₀ кнопку «Сброс» отпускаем, т.е. S=R=1, включаются D-триггера. Передний фронт первого тактового импульса, поступающего на С – вход первого (левого) триггера переписывает 1 с D – входа на Q₀ – выход. На  уровень изменится из 1 в 0 – это задний фронт и С – вход второго триггера его не ощущает, поэтому 2 и 3 триггера своего состояния не изменят. В результате поступления первого тактового импульса имеем: Q₀=1, Q₁=0, Q₂=0. Второй тактовый импульс перепишет 0 с D – входа на выход Q₀,   изменит свое состояние из 0 в 1 – это передний фронт, который подается на С – вход второго триггера, поэтому 1 с D – входа второго триггера перепишется на Q₁ – выход,  изменит свое состояние из 1 в 0 – задний фронт, поэтому третий триггер своего состояния не изменит. В результате имеем, Q₀=0, Q₁=1, Q₂=0. Нетрудно видеть, что двоичный счетный код на выходе счетчика точно равен количеству (N) тактовых импульсов от ГТИ на входе счетчика.

Длина счетчика – величина, которая указывает на максимальное число, до которого может считать счетчик и  определяется количеством счетных триггеров в счетчике. В нашем случае длина счетчика равна 2³=8 (2^N).

 

счетчик на вычитание

Строится так же, как и счетчик на сложение с той лишь разницей, что каждый следующий триггер тактируется не от инверсного выхода предыдущего, а от прямого выхода.

 

 

 

 

 

 

 

 

N	Q2	Q1	Q0
0	0	0	0
1	1	1	1
2	1	1	0
3	1	0	1
4	1	0	0
5	0	1	1
6	0	1	0
7	0	0	1
8	0	0	0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

реверсивный счетчик

 

Это такой счетчик, направление счета которого может быть изменено под действием управляющих сигналов. Заметим, что счетчик на сложение отличается от счетчика на вычитание тем, что каждый следующий триггер тактирует не от прямого выхода предыдущего, а от инверсного выхода предыдущего.  Т.е. схема реверсивного счетчика должна уметь коммутировать (переключать) тактирующий вход следующего триггера к прямому или инверсному выходам предыдущего.

 

 

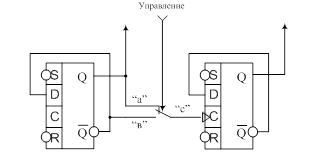
Схема ключа «Управление» состоит из одного инвертора, 2 элементов 2 – И и одного элемента 2 – ИЛИ. При положении ключа «Управление» нормально замкнутым контакт  +5В. На 2 вход верхнего элемента 2 – И поступает 1, а на второй вход нижнего элемента 2 – И через инвертор подается 0. В соответствии с таблицей истинности для элемента 2 – И на выходе нижнего элемента, в независимости от того чему равно «в», будет 0, выход верхнего элемента 2 – И будет равен «а». Докажем это. Если «а»=0, то , т.е. «а». Если «а»=1,то , т.е. «а». На выходе элемента 2 – ИЛИ будет 0 + «а», т.е. «С» = «а». Если ключ «Управление» переключить, то на 2 верхнем входе элемента 2 - И будет 0 и на выходе его будет 0. На втором входе нижнего элемента 2 – И через инвертор подается 1, следовательно, выход этого элемента будет равен «в». 0 + «в» на элементе 2 – ИЛИ на выходе даст «в» = «С». И в этом случае на С – вход следующего триггера подаются тактирующие импульсы от инверсного выхода предыдущего триггера, счетчик будет работать на сложение.

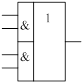 В качестве коммутирующего элемента использовали элемент 2 – 2И – ИЛИ.

 

 

 

 

 

 

 

 

 

 

 

 

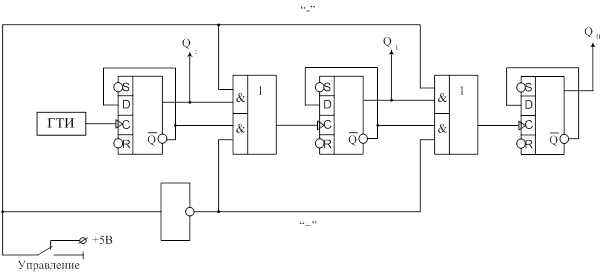
счетчик заданной длины

 

         Часто бывает необходимо, чтобы счетчик считал не только до числа 2^N, где N – количество счетных триггеров в счетчике, а мог бы считать до любого меньшего числа, после чего остановиться или начать счет с нуля.

         Рассмотрим, например, счетчик, который считает до 12, после чего сбрасывается и начинает счет заново.

 

 

 

 

 

Толстой линией на схеме изображена так называемая ШИНА. Такой способ используется в тех случаях, когда на схеме много соединений, которые если показать сильно затруднят чтение схемы. Шина представляет собой условное обозначение жгута проводников (изолированные друг от друга), каждый из которых присвоен номер на входе и такой же на выходе.

RS – триггер в конце нужен для того, чтобы 4 D – триггера работали одинаково, т.к. они не совершенны и сбрасывают за разное время.

Схема управления этим счетчиком состоит из элемента 4 – И – НЕ и RS – триггера. Входа элемента 4 – И – НЕ подключены к соответствующим прямым или инверсным выходам триггеров счетчика. Т.к. схема 4 – И – НЕ должна срабатывать только на заданной кодовой комбинации (например, 1100), то правила подключения его входов к счетчику следующие: если данный разряд кодовой комбинации =1, то этот вход элемента 4 – И – НЕ подключается к прямому выходу соответствующего триггера; если разряд в числе =0, то соответствующий вход элемента 4 – И – НЕ подключается к инверсному выходу соответствующего триггера.

В примере 2 младших разряда равны 0, поэтому 1-й и 2-й входа элемента 4 – И – НЕ подключены к инверсным выходам 2 триггеров счетчика. 

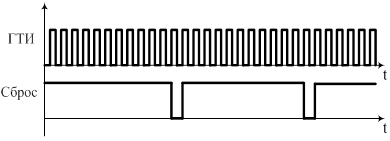
Когда счетчик досчитает до заданного числа (на прямых выходах триггеров считывается заданная кодовая комбинация) за счет правильного подключения  4 – И – НЕ на его входах будет четыре 1, следовательно, на выходе 0. Этот ноль подается на S – вход RS – триггера. На R – входе в это время от ГТИ - 1. Следовательно, на инверсном выходе RS – триггера - 0. Этот 0 подается на все R – входа триггеров счетчика. Если хотя бы один из триггеров изменит свое состояние на противоположное, то на выходах элемента  4 – И – НЕ уже не будет 4-х единиц. Следовательно, на выходе будет 1, т.е. в этот момент времени у RS – триггера S=1 и R=1 по правилам его работы он сохраняет предыдущее состояние. Через некоторое время от ГТИ на R – вход RS – триггера поступит 0 (S=1) и RS – триггер опрокинется, т.е. на инверсном выходе 1, следовательно, на всех R – входах триггеров счетчика 1 и счетчик начинает считать заново.

 

линейные дешифраторы

 

Это устройство, имеющее избирательно реагировать на заданные входные ситуации (события).

Для цифровых систем линейная дешифрация означает, что некой заданной кодовой комбинации на входе будет соответствовать определенная реакция на выходе.

Линейный дешифратор на 10

Выход каждого из элемента 4 – И является соответствующим выходом дешифратора. Например, 1-ый элемент D₁ декодирует кодовую (входную) комбинацию 4 нуля, т.е. на его выходе должна быть 1, а на всех остальных выходах дешифратора - 0. Для того чтобы на выходе D₁ был 0 необходимо на его входах иметь 4 единицы, поэтому его входа подключены к соответствующим выходам инверторов. Если соответствующий разряд на кодовом входе равен 0, то на некоторый элемент 4 – И мы его подаем через инвертор. Если разряд равен 1, то он подключается к соответствующему элементу непосредственно.

 

 

 

 

 

 

 

 

 

 

 

 

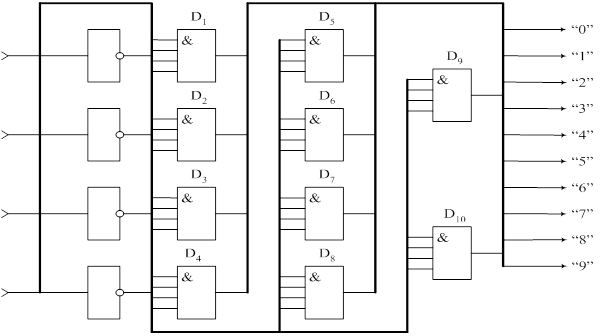
На схемах электрических принципиальных дешифраторы изображают так: